Закон Брэдфорда «о рассеянии информации»

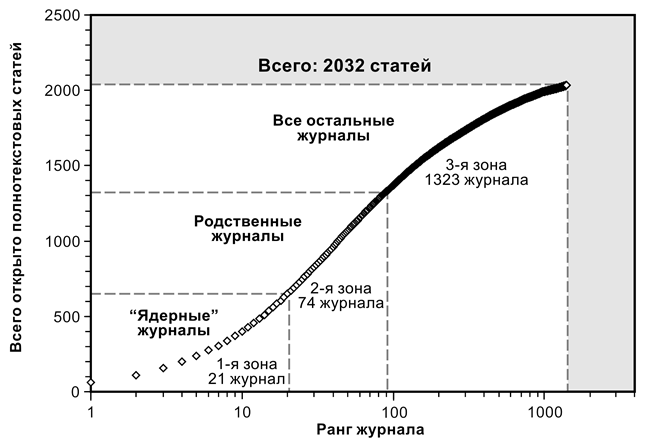
Самюэль Брэдфорд сформулировал свой закон на основе анализа библиографии по геофизике (1332 статьи). Выборка включала статьи из 326 журналов, которые распределялись по трем зонам, содержащим приблизительно равное число статей:

• в первую зону (зону ядра) входят профильные журналы,
непосредственно посвященные заданному вопросу (9 журналов, 429 статей);

•  во вторую зону входят «родственные» журналы, частично посвященные
заданному вопросу (59 журналов, 499 статей);

•  в самую многочисленную третью зону входят журналы, тематика которых
далека от заданного вопроса (258 журналов, 404 статьи).

• Соотношение числа журналов

• в этих зонах 1: n: n²

 

Закон Ципфа «о распределении слов»

Закон Ципфа — эмпирическая закономерность распределения частоты слов естественного языка: если все слова языка (или просто достаточно длинного текста) упорядочить по убыванию частоты их использования, то частота n -го слова в таком списке окажется приблизительно обратно пропорциональной его порядковому номеру n (так называемому рангу этого слова). Например второе по используемости слово встречается примерно в два раза реже, чем первое, третье — в три раза реже, чем первое, и т. д.

Закон носит имя своего первооткрывателя — американского лингвиста Джорджа Ципфа из Гарвардского университета.

Если слова любого текста ранжировать по частоте использования, то произведение ранга на частоту есть величина постоянная:

F*R =C,

где: F – частота появления слова в тексте;

R – ранг слова (наиболее часто употребляемое слово получает ранг 1, следующее – 2 и т.д.);

С – константа.

У гиперболы есть замечательно свойство. Если для обеих осей взять логарифмический масштаб, то гипербола будет иметь вид прямой:

Мандельброт немного модифицировал формулу Ципфа

F = C * R ^-1/a,

Где a – коэффициент, характеризующий богатство словарного запаса;

чем больше значение a, тем богаче словарный запас текста, поскольку кривая зависимости частоты появления каждого слова от его ранга убывает медленнее, и, например, редкие слова появляются чаще, чем при меньших значениях a.

Именно это свойство Мандельброт предполагал использовать для оценки эрудиции.

С законом Ципфа не всё так гладко, и в конкретных применениях опираться на экспериментально определенный коэффициент a не всегда получается.

В то же время закон Ципфа является ни чем иным, как законом Парето «наоборот», поскольку и тот и другой – частные случаи степенных рядов, или… проявление фрактальной природы экономических и социальных систем.

Сетевой эффект

В экономике и бизнесе сетевым эффектом (или сетевой экстерналией) называется эффект, который пользователь товара или услуги оказывает на ценность этого продукта или услуги для других пользователей. Классическим примером проявления сетевого эффекта является телефонная сеть.

Чем больше пользователей владеют телефонами, тем более ценным является использование сети для каждого её пользователя.

Ценность возрастает при возрастании количества абонентов, так как подключение каждого дополнительного абонента означает возможность связаться с большим количеством людей.

Это пример положительной экстерналии, потому что пользователь может приобретать телефон без намерения создавать ценность для других пользователей, но, подключаясь к сети, ненамеренно создает её. Характер положительного сетевого эффекта выражается законом Меткалфа, который утверждает, что ценность сети возрастает пропорционально квадрату числа её пользователей.

Выражение «сетевой эффект» часто применяется в позитивном смысле. Однако сетевые экстерналии могут быть и отрицательными, например перегрузка компьютерной сети или пробки на дорогах.

 

 

 

 

СОЦИАЛЬНАЯ ИНЖЕНЕРИЯ

 

Лекция 6. Использование коммуникационных стилей в социальной инженерии

Вопросы лекции

Понятие коммуникации.