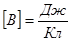Работа сил электростатического поля при перемещении заряда. Потенциал

 

Определим работу по перемещению заряда Q₀ из точки 1 в точку 2, совершаемую полем заряда Q (рис. 3.7).

 

Рис.3.7

 

Так как при движении заряда Q₀ сила взаимодействия его с зарядом Q, создающим поле, по закону Кулона зависит от расстояния r:

,

то сначала определим элементарную работу dA на бесконечно малом участке dℓ:

dA=Fdℓcosα,

здесь α – угол между векторами F и dℓ. Учитывая, что dℓcosα=dr, найдем полную работу как интеграл:

(3.13)

Отсюда следует, что работа электрического поля не зависит от формы пути, а определяется начальным и конечным положениями заряда Q₀. Это означает, что электростатическое поле является потенциальным, а его силы – консервативными.

Из (3.13) следует, что работа, совершаемая при перемещении заряда в электростатическом поле вдоль любого замкнутого контура, равна нулю, то есть:

Последнее равенство можно записать, учитывая, что ,

Тогда для электростатического поля имеем:

,

где Е_ℓ=Е сosα – проекция вектора Е на перемещение dℓ.

Этот интеграл называется циркуляцией вектора напряженности. Для электростатического поля циркуляция вдоль любого замкнутого контура равна нулю.

Из раздела “механика” известно, что работа консервативных сил равна убыли потенциальной энергии:

А₁₂=W_n1 – W_n2.

Сравнивая это равенство с (3.13), получим формулу потенциальной энергии заряда Q₀, находящегося в поле заряда Q:

По мере удаления от заряда Q потенциальная энергия убывает и можно принять, что в бесконечности W_п=0, тогда постоянная интегрирования

С = 0

 

(3.14)

Отношение W_п/ Q ₀ не зависит от заряда и может служить энергетической характеристикой поля, называемой потенциалом поля в данной точке, созданным зарядом Q:

(3.15)

Из формул (3.14) и (3.15) следует, что потенциал поля точечного заряда (шара) Q:

(3.16)

Работа, совершаемая электрическими силами по перемещении заряда Q₀ из точки 1 в точку 2, может быть вычислена через разность потенциалов:

А₁₂ = W_п1 – W_п2 = Q₀ (φ₁ – φ₂)(3.17)

Если точка 2 находится в бесконечности, то φ₂ = 0 и следовательно,

А₁₂ = φ₁Q₀,

откуда

, (3.18)

где Q₀ -величина перемещаемого в поле заряда.

Таким образом, потенциал данной точки поля определяется работой, совершаемой силами поля при перемещении единичного заряда из этой точки в бесконечность. За единицу потенциала принят Вольт:

Знак потенциала определяется знаком заряда, создающего поле. Если поле образовано системой зарядов, то его потенциал равен алгебраической сумме потенциалов полей всех зарядов (принцип суперпозиции):

 

Точки пространства с равными потенциалами образуют поверхность, называемую эквипотенциальной. Такой поверхностью, например, является поверхность равномерно заряженной проводящей сферы.

Работа при переменном заряде Q вдоль эквипотенциальной поверхности A= Q Δφ=0.