Круговые процессы. Второе начало термодинамики.

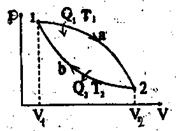
Круговым процессом, или циклом, называется такой процесс, когда система, пройдя через ряд промежуточных состояний, возвращается в исходное состояние. Графически круговой процесс изображен на рис. 6.8 замкнутой кривой и состоит из участка расширения (1а2) и сжатия (2b1).

 

Рис.6.8

 

Для расширения газу от тела с температурой Т₁, называемого нагревателем, сообщается количество теплоты Q₁. В процессе сжатия газ отдает количество теплоты Q₂ телу с температурой Т₂ < Т₁, называемому холодильником.

Если цикл идет по часовой стрелке, то он называется прямым. Положительная работа расширения А, совершаемая газом и численно равная площади фигуры (V₁ 1a2V₂), больше отрицательной работы сжатия А₂, совершаемой над газом и выражаемой площадью фигуры (V₂ 2b1V₁). Следовательно, работа А, совершенная за цикл и численно равная площади фигуры(1а2b1), будет положительна:

А = А₁ – А₂ > 0

Прямой цикл используется в тепловых машинах – периодически действующих устройствах, превращающих тепло, полученное от нагревателя, в работу А.

Так как в результате кругового процесса система возвращается в исходное состояние, то изменение внутренней энергии, как функции состояния, ΔU = 0.

Следовательно, согласно первого закона термодинамики (6.21) для кругового процесса

Q = A

Учитывая, что Q = Q₁ – Q₂, имеем:

А = Q₁ – Q₂

Определим термический коэффициент полезного действия цикла, как отношение работы А к полученной системой теплоте:

(6.46)

Может ли КПД теплового двигателя быть равен 100 %?

Это будет (согласно 6.46) только, если Q₂ = 0. Как показал С. Карно, такое невозможно: для работы теплового двигателя необходимо часть тепла, полученного от нагревателя, отдать холодильнику. Это утверждение о невозможности создания теплового двигателя, работающего с одним только источником теплоты (вечный двигатель второго рода) составляет содержание второго закона термодинамики: невозможен вечный двигатель второго рода, т.е. процесс, единственным результатом которого было бы превращение теплоты, полученной от нагревателя, в работу.

Цикл (рис.6.8) может идти и против часовой стрелки. Тогда его работа будет отрицательна. Такой цикл называется обратным и используется в холодильных машинах для переноса (за счет работы внешних сил) теплоты от тела с более высокой температурой к телу с температурой более низкой. Процесс перехода системы из состояния 1 в состояние 2 называется обратимым, если после возвращения системы в исходное состояние ни в системе, ни в окружающей среде никаких изменений не происходит. Любой процесс, не удовлетворяющий этим условиям, называется необратимым.

Все реальные процессы необратимы. Примером необратимости является процесс теплообмена, при котором теплота самопроизвольно переходит от горячего тела к холодному, однако обратного самопроизвольного процесса произойти не может.

Таким образом, обратимые процессы – понятие идеализированное. Однако их изучение важно, поскольку многие реальные процессы в природе и технике близки к обратимым, и именно они являются наиболее экономичными.

 

Цикл Карно

 

Основываясь на втором законе термодинамики, С. Карно доказал, что из всех тепловых машин наибольшим КПД обладают обратимые машины. Самым экономичным является круговой процесс, состоящий из двух изотерм и двух адиабат (рис.6.9), названный циклом Карно.

Можно показать, что КПД цикла Карно определяется только температурами нагревателя Т₁ и холодильника Т₂:

(6.47)

 

Рис.6.9

 

Как следует из (6.47), для повышения η необходимо увеличивать разность температур Т₁ нагревателя и Т₂ холодильника.

 

Энтропия

Из формул (6.46) и (6.47) следует, что и

Учтем, что количество тепла Q₂, отданного холодильнику отрицательно. Тогда последнее равенство можно записать:

(6.48)

Отношение Q/T называется приведенной теплотой.

Приведенная теплота, переданная системе нагревателем, при бесконечно малом ее изменении, равна δQ/Т. Можно показать, что для любого обратимого кругового процесса сумма приведенных теплот равна нулю. Тогда выражение (6.48) в общем, виде может быть записано как:

(6.49)

Равенство нулю интеграла по замкнутому контуру означает, что в обратимом процессе подинтегральное выражение есть полный дифференциал некоторой функции S, зависящей только от состояния системы. Функция S называется энтропией.

Таким образом

(6.50)

Из формулы (6.49) следует, что для обратимых процессов изменение энтропии

ΔS = 0 (6.51)

Можно показать, что для необратимых неравновесных процессов, происходящих в замкнутой системе, энтропия возрастает

ΔS > 0 (6.52)

Соотношения (6.51) и (6.52) объединяются в неравенство Клаузиса:

ΔS≥0

т.е. энтропия замкнутой системы либо возрастает, либо остается постоянной.

Так как реальные процессы необратимы, то можно утверждать, что все процессы, протекающие в замкнутой системе, ведут к увеличению энтропии. Это утверждение, называемое принципом возрастания энтропии, является еще одной формулировкой второго закона термодинамики.

Физический смысл энтропии выяснил Л. Больцман, который показал, что энтропия связана с термодинамической вероятностью состояния системы. Термодинамическая вероятность w определяется как число способов, которыми может быть реализовано данное состояние системы. Согласно Больцману, связь S и w выражается формулой:

S = k lnw (6.53)

где k – постоянная Больцмана.

Когда достигается равновесное состояние системы, то в этом состоянии система может оставаться сколь угодно долго, т.е. параметры системы не меняются и в системе отсутствуют потоки энергии или вещества. Если потоки имеют место, то изменение внутренней энергии dU может происходить не только за счет сообщения системе теплоты δQ и совершения над ней работы δА, но и за счет переноса массы. Тогда первый закон термодинамики можно записать в более общей форме

dU = δQ – PdV + μdn,

где называется химическим потенциалом и представляет изменение энергии системы, приходящейся на одну частицу, участвующей в переносе при V = const и S = const.

 

 

Фазовые превращения

 

Фазой называется термодинамически равновесное состояние вещества, отличаются не химическим составом, а физическим свойствами от других равновесных состояний того же вещества (например, вода может находиться в трех фазах: жидком, твердом и в виде пара). Переход вещества из одной фазы в другую называется фазовым переходом.

Различают фазовые переходы I и II рода. Фазовый переход I рода связан с поглощением или выделением тепла (например, плавление и кристаллизация). Фазовый переход II рода не связаны с теплотой (например, переход некоторых веществ при определенных температурах в сверхпроводящее состояние см. п.5.7).

Для характеристики фазовых переходов используются диаграммы состояний (обычно в координатах Р – Т). На этих диаграммах можно найти точку одновременного равновесного осуществления трех фаз – тройную точку. Например, тройная точка для воды 273,16 К. Термодинамика позволяет рассчитать равновесие двух фаз одного вещества, пользуясь уравнением Клапейрона – Клаузиуса:

,

где производная от равновесного давления по температуре зависит от теплоты фазового перехода λ, температуры перехода и изменения объема фаз (например, при замерзании воды ее объем возрастает).