
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экспериментальное обоснование основных идей квантовой механики. Взаимодействие фотонов с электронамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Нагретые тела испускают электромагнитное излучение определенной интенсивности и спектра. При невысоких температурах это излучение приходится на область невидимых инфракрасных волн. С повышением температуры длина волн излучения уменьшается и при температурах ~1000 К переходит в видимую область (тела светятся от красного до белого каления). Тепловое излучение -это излучение нагретыми телами, находящимися в состоянии теплового равновесия с окружающими телами (равновесное излучение). Основные характеристики теплового излучения: а) мощность (или поток) излучения Фе - энергия, излучаемая телом за 1 секунду; б) энергетическая светимость R-энергия, излучаемая с 1 м2 поверхности тела за 1 секунду
где S-площадь излучающей поверхности тела; в) энергетическая освещенность Ее - энергия, падающая на 1 м2 поверхности в 1 секунду; г) спектральная плотность энергетической светимости (излучательная способность) rλ
т.е. мощность теплового излучения с единицы площади излучающей поверхности, приходящаяся на единичный интервал длин волн (в интервале от λ до λ+dλ). д) коэффициент поглощения (поглощательная способность) αλ
где Фλ -мощность энергии, падающей на тело,
е) коэффициент отражения ρλ ρλ = 1 - αλ (5.4) определяет долю отраженной энергии от всей падающей. Закон Кирхгофа. Опыт показывает, что в состоянии теплового равновесия (при Т=const) отношение спектральной плотности энергетической светимости rλ к коэффициенту поглощения αλ для разных тел одинаково и зависит только от температуры Т и длины λ
Тело, которое при любой температуре поглощает всю падающую на него энергию независимо от длины волны λ, называется абсолютно черным. Для него αλ=1. Закон Кирхгофа определяет отношение спектральной плотности энергетической светимости тела к его поглощательной способности, которое зависит от материала тела, является функцией только температуры и длины волны. Из закона следует, что всякое тело преимущественно поглощает те лучи, которые оно в наибольшей степени само излучает. Кирхгоф предложил модель абсолютно черного тела - ящик с отверстием (отверстие-модель черного тела). Эксперименты показали, что зависимость r (λ, Т) при различных температурах Т черного тела имеет вид, изображенный на рисунке 5.1.
Рис.5.1
Закон Стефана-Больцмана: энергетическая светимость R абсолютно черного тела пропорциональна четвертой степени его термодинамической температуры Кельвина: R= где Закон смещения Вина: длина волны λmax, на которую приходится максимум спектральной плотности rλ энергетической светимости (рис.5.1), обратно пропорциональна температуре Т
где Попытки объяснить ход экспериментальной кривой rλ - Т (рис.5.1), пользуясь классической теорией, не дали положительных результатов (они приводили к выводу, что с уменьшением λ величина rλ должна неограниченно возрастать, что противоречило эксперименту). В 1900 г. Макс Планк выдвинул гипотезу, что энергия излучается и поглощается квантами. Он дал новое объяснение ходу кривой на рис.5.1, которое не расходилось с опытом. Так было положено начало квантовой теории. Согласно этой теории, нагретые твердые, жидкие и газообразные тела излучают энергию в виде квантов с различной частотой
где ε- квант энергии (для оптического диапазона частот квант h- постоянная Планка (h = 6,62·10-34 Дж·с) Длина волны λ излучения связана с частотой ν соотношением
где с – скорость света в вакууме (c=3·108 м/с). Импульс фотона может быть выражен через частоту ν и длину волны λ
где m-масса фотона. Фотон в отличие от натуральных частиц (электронов, протонов и др.) не имеет массы покоя, он существует только в движении. В этом его принципиальное отличие от натуральных частиц. Созданы приборы, предназначенные для измерения очень высоких температур (Т>2000 К) на основе законов теплового излучения - оптические пирометры.
Внешний фотоэффект
Фотоэлектрическим эффектом называют вырывание электронов с поверхности твердых тел фотонами. Это явление открыто в 1887 г. Герцем и изучено в 1888 г. Столетовым.
а) б) Рис. 5.2
На (рис.5.2,а) показана схема для наблюдения фотоэффекта. Свет через кварцевое стекло направляется в вакуумный баллон и падает на катод К. Вырванные светом электроны под действием электрического поля устремляется к аноду А. Гальванометр G показывает возникновение в цепи электрического тока. Если свет направить на анод вместо катода, то тока не наблюдается. Величину фототока I можно изменять, изменяя с помощью потенциометра П напряжение между катодом и анодом. Вольт - амперная характеристика фотоэлемента показана на рис.5.2,б. В закономерностях этого явления отчетливо проявляются квантовые свойства света. Для вырывания электрона из атома на поверхности твердого тела надо совершить определенную работу А, называемую работой выхода электрона. Для каждого металла работа выхода является определенной величиной. Если на металл падает свет, то энергия фотона передается электрону и у электрона может оказаться энергия, достаточная для совершения работы выхода. hν ³ А (5.10) Таким образом, фотоэффект может наблюдаться только тогда, когда энергии фотона hν достаточно для вырывания электрона. Иначе говоря, когда частота света не меньше некоторой величины ν0, называемой красной границей фотоэффекта,она определяется равенством: Пользуясь законом сохранения энергии, можно установить связь между энергией фотона hν, работой выхода электрона А и максимальной кинетической энергией вылетевшего электрона Екmax - формула Эйнштейна для фотоэффекта:
где m-масса электрона ( Vmax-максимальная скорость фотоэлектрона. Вид вольт - амперной характеристики свидетельствует, что электроны покидают металл со скоростью, отличной от нуля (при U=0 фототок не равен нулю). Для того, чтобы фототок стал равным нулю, нужно приложить задерживающее напряжение. При таком напряжении ни одному из электронов, не удается преодолеть задерживающее поле и достигнуть анода.
Измерив задерживающее напряжение U3, можно определить максимальное значение скорости V фотоэлектронов (или их кинетической энергии). Из (рис.5.2,б) видно, что величина фототока I растет с увеличением напряжения U между катодом и анодом, и достигает (при неизменной интенсивности света) некоторого максимального значения Iн – тока насыщения. Это возможно, когда все электроны, выбитые светом, достигают анода. Исследования Столетова привели к установлению законов фотоэффекта (их можно объяснить и с помощью формулы Эйнштейна (5.11), полагая, что каждый фотон может вырвать не более одного электрона): 1. Сила тока насыщения (следовательно, и количество электронов, испускаемых в единицу времени при фотоэффекте), пропорциональна интенсивности падающего света, т.е. количеству фотонов, падающих в единицу времени на единицу поверхности металла (при выполнении условия 5.10); 2. Максимальная скорость (кинетическая энергия) фотоэлектронов зависит от частоты света, но не зависит от его интенсивности. Основанные на фотоэффекте вакуумные фотоэлементы находят применение в технике. Рассмотренный выше фотоэффект можно назвать однофотонным. Если в качестве источника света взять мощный лазер, то возникает многофотонный фотоэффект (но это относится в внутреннему фотоэффекту в полупроводниках или в газах).
Эффект Комптона
Еще более отчетливо квантовые свойства света проявляются в Комптон - эффекте. Эффект Комптона заключается в увеличении длины волны рентгеновских лучей, рассеянных на электронах некоторых веществ на
Δλ=λ 1 -λ=λк(1-cosθ) (5.13) где λ - длина волны падающего фотона с энергией λ1 - длина волны фотона, рассеянного на угол λк - постоянная Комптона (комптоновская длина волны при рассеивании на электроне λк = 2,436·10-12 м). Увеличение длины волны (λ1>λ) Комптон объяснил взаимодействием фотона со свободным электроном, в результате чего часть энергии Ее фотон передает электрону ε1= ε2+ Ее, т.е. ε2<ε1
Кроме закона сохранения энергии, выполняется и закон сохранения импульса.
Рис.5.3 Давление света Давление света на тела было впервые измерено Лебедевым (1898 г.). Объясним его с квантовой точки зрения. Пусть на поверхность непрозрачного тела падает поток N фотонов в единицу времени. Если коэффициент отражения поверхности ρ, то ρ N число фотонов отразится, (I- ρ)N- поглотится. Каждый отраженный фотон сообщит поверхности импульс (см. формулу 5.9), а
все отраженные ρN фотонов:
Поглощенный фотон передаст свой импульс телу (1-ρ)N И те и другие фотоны в итоге передадут поверхности импульс 2
Так как изменение импульса тела численно равно давлению Рg, то давление, оказываемое светом на поверхность (при нормальном падении) Рg = N Величина Nhν=Ee называется энергетической освещенностью. Тогда ω - объемная плотность энергии излучения (ω = n·ε, где n – объемная плотность фотонов). У зеркальной поверхности коэффициент отражения ρ = 1, у черной ρ=0, поток излучения Фе = Ее S = εN = hν · N. Максвеллом давление света было объяснено с волновых позиций, им была получена формула, подобная (5.14). Заключение: рассмотренные выше волновые свойства электромагнитных волн в том числе и (света): интерференция, дифракция, поляризация и др., неразрывно связаны и c корпускулярными свойствами, наглядно проявляемыми в явлениях фотоэффекта, эффекта Комптона и др. Это подтверждает диалектическое единство этих свойств в природе (см. п. 5.2).
|
||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 907; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |

 , (5.1)
, (5.1) , (5.2)
, (5.2) , (5.3)
, (5.3) -мощность, поглощенная телом;
-мощность, поглощенная телом; (5.5)
(5.5)
 Т4, (5.6)
Т4, (5.6) - постоянная Стефана-Больцмана.
- постоянная Стефана-Больцмана. , (5.7)
, (5.7)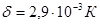 -постоянная смещения Вина.
-постоянная смещения Вина. , которую можно определить по формуле Планка:
, которую можно определить по формуле Планка: , (5.8)
, (5.8)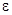 называется фотоном)
называется фотоном)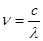 ,
, , (5.9)
, (5.9)
 . Граничной частоте соответствует и граничная длина волны
. Граничной частоте соответствует и граничная длина волны  . Для большинства металлов (кроме щелочных) красная граница лежит в ультрафиолетовой области спектра.
. Для большинства металлов (кроме щелочных) красная граница лежит в ультрафиолетовой области спектра. или
или  , (5.11)
, (5.11) );
); = еU3, (5.12)
= еU3, (5.12) ;
; , энергия его
, энергия его  ;
;
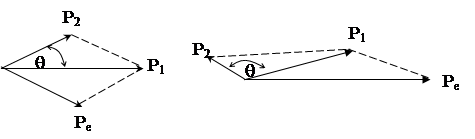 Величина энергии Ее и импульса Ре, переданных электрону, зависят от угла рассеяния
Величина энергии Ее и импульса Ре, переданных электрону, зависят от угла рассеяния 

 , а все (1- ρ)N фотонов
, а все (1- ρ)N фотонов N
N  , (5.14)
, (5.14)


