Проблема квантового измерения

 

Квантовое измерение – это процесс, во время которого одна квантовая система получает информацию о другой. Например, в случае частицы и датчика в двухщелевом эксперименте обозначим как |левая> и |правая> состояния (волны), в которых частица проходит через левую либо через правую щель соответственно, и пусть |есть щелчок> и |нет щелчка> будут состояниями (волнами), в которых датчик щелкает, регистрируя проходящую частицу, или не щелкает. Обозначим также как |готов> состояние датчика до измерения, в котором он готов обнаружить частицу, если эта частица пройдет через правую щель. Непосредственно перед измерением частица находится в суперпозиции состояний |левая> + |правая>, а датчик находится в состоянии |готов>. Во время измерения в компоненте |левая> этой суперпозиции частица проходит через левую щель, и датчик не щелкает, а в части |правая> частица проходит через правую щель, и датчик щелкает. Значит, сразу после измерения состояние частицы и датчика описывается суперпозицией |левая, нет щелчка> + |правая, есть щелчок>. Таким образом, и частица, и датчик находятся в запутанном состоянии, которое является суперпозицией состояний «частица прошла через левую щель», коррелированным с «датчик не щелкнул», и «частица прошла через левую щель», коррелированным с «датчик щелкнул».

Предположим, я нахожусь в комнате в то время, когда проводится эксперимент с двойной щелью, и я либо слышу щелчок, либо нет. Я также являюсь квантовой системой, хотя и состоящей из множества частей. Пусть |Сет Ллойд слышит щелчок> будет волной, соответствующей состоянию, когда я слышу щелчок, а |Сет Ллойд не слышит щелчка> будет волной, соответствующей состоянию, когда я не слышу щелчка. (Обратите внимание, это довольно сложные волны, соответствующие всем атомам моего тела.)

После того как звук (если он был) достиг моего уха, состояние системы, содержащей частицу, датчик и меня, будет |левая, нет щелчка, Сет Ллойд не слышит щелчка > + |правая, есть щелчок, Сет Ллойд слышит щелчок>. Теперь я запутан с частицей и датчиком. В этом запутанном состоянии можно видеть, что мое состояние относительно частицы, находящейся справа, и щелчка датчика будет |Сет Ллойд слышит щелчок>. Мое состояние относительно частицы, находящейся слева, и отсутствия щелчка датчика будет |Сет Ллойд не слышит щелчка>. В квантовом лесу упало квантовое дерево, и квантовый кто-то это услышал.

Эта картина «относительного состояния» процесса квантового измерения иллюстрирует само явление измерения. Информация, о том, через какую щель прошла частица, заражает сначала датчик, а потом меня. Если я напишу вам письмо о том, услышал ли я щелчок, то, когда вы его получите, ваше относительное состояние отразит то, что произошло: |Сет Ллойд написал мне, что он услышал щелчок> или |Сет Ллойд написал мне, что он не слышал щелчка>. Теперь вы запутаны с частицей, с датчиком и со мной. После измерения информация о его результатах распространяется и заражает все, с чем контактирует.

 

 

Заменим в двухщелевом эксперименте обе щели кнопками. Если нажать первую кнопку, кот получит молоко; если нажать вторую кнопку, тот же самый кот получит яд. Но квантово-механическая частица нажимает обе кнопки одновременно: кот Шрёдингера и жив, и мертв одновременно!

 

Несмотря на то что картина относительных состояний квантового измерения иллюстрирует это явление, все же остаются некоторые вопросы. Когда я слышу щелчок, что происходит с другой частью суперпозиции, в которой я не слышал щелчка? Тот человек, который не слышал щелчка, – это все еще я? А может быть, я и слышал щелчок, и не слышал его в одно и то же время? Этот тревожный аспект описанной картины усилил в 1935 г. австрийский физик Эрвин Шрёдингер. Он предположил, что, когда датчик щелкает, он запускает механизм, убивающий кота. В парадоксе кота Шрёдингера состояния частицы, датчика и кота после измерения обозначается как |левая, нет щелчка, кот жив> + |правая, есть щелчок, кот мертв>. Каким-то странным квантовым образом кот и жив, и мертв в одно и то же время.

Парадокс кота Шрёдингера породил много заблуждений. Стивен Хокинг так устал от него, что часто говорил (перефразируя Йозефа Геббельса): «Когда я слышу слова “кот Шрёдингера”, я хватаюсь за пистолет». Первоначальная разгадка парадокса, предложенная Бором, состояла в том, что, когда мы слышим щелчок и кот умирает, другая часть суперпозиции – та, в которой мы не слышим щелчка и кот остается жив – просто исчезает. Такое исчезновение частей волны, которых мы не видим в опыте, – пример коллапса волновой функции, о котором мы говорили выше. Волна здесь, в сущности, коллапсирует в один из своих компонентов. В картине коллапса волновой функции квантового измерения к тому времени, как я напишу вам и сообщу, что я услышал щелчок, а когда обернулся, то увидел, что кот мертв, та часть волны, в которой кот все еще жив, исчезнет.

Проблема с этим решением, как мы уже видели, состоит в том, что динамические законы квантовой механики обратимы. Принципиально возможно вернуться в исходное состояние, существовавшее до измерения. Но если волновая функция действительно коллапсирует, вернуться в исходное состояние становится невозможно. В то же время известно, что во многих случаях, таких как эффект спинового эха и его аналоги, можно обратить динамическую эволюцию квантовой системы из многих частей и вернуть ее в исходное состояние. Как теория, так и эксперимент делают коллапс волновой функции неприемлемым решением проблемы измерения.

К счастью, есть простая и изящная альтернатива объяснению с помощью коллапса волновой функции. Проблема измерения возникает из-за присутствия тех частей волновой функции, что соответствуют альтернативам, которые на самом деле не случаются. Было бы неплохо иметь возможность просто проигнорировать их. Иначе говоря, когда датчик щелкнул и я написал вам о смерти кота, я хотел бы покончить с этим делом и перестать беспокоиться о тех частях волновой функции, в которых кот все еще жив. Пусть прошлое останется в прошлом. В каком случае мы можем себе позволить проигнорировать эти части волновой функции? Ответ на этот вопрос дали Роберт Гриффитс и Роланд Омнес и дополнили Мюррей Гелл-Манн и Джеймс Хартл: остальные части волновой функции можно проигнорировать в тот момент, когда они не оказывают на нас никакого дальнейшего влияния.

Такое решение проблемы измерения зависит не только от настоящего, но и от будущего. Если другие части волновой функции никогда больше не пересекутся с нашими, то мы говорим, что будущая история волновой функции декогерирует. Этот подход в квантовой механике изящно устраняет большинство тревожных аспектов проблемы измерения.

В случае двухщелевого эксперимента, например, есть две возможных истории. В одной из них частица проходит через левую щель и попадает на стену. В другой частица проходит через правую щель и тоже попадает на стену. Эти истории являются когерентными: они взаимодействуют друг с другом, создавая интерференционные полосы на стене.

Теперь добавим к правой щели датчик. У нас по-прежнему две возможные истории. В одной из них частица проходит через левую щель и попадает на стену. В другой частица проходит через правую щель, вызывает срабатывание датчика и попадает на стену. Из-за датчика интерференционная картина исчезает. Эти две истории декогерентны: они друг с другом не смешиваются. Сходным образом в парадоксе кота Шрёдингера, после того как датчик щелкнул и кот умер, нет больше смысла смотреть на кота и проверять, мертв ли он. Смотри или не смотри, это не имеет никакого значения для будущего: кот остается мертвым. Следовательно, истории этого эксперимента – декогерентны. В этом случае мы можем сказать, что кот или жив, или мертв, но не жив и мертв одновременно.

Существует простой критерий, позволяющий решить, является ли некий набор историй когерентным или декогерентным. Вспомним, что происходит, когда мы делаем измерение. Да, измерение разрушает когерентность. Но оно не может разрушить когерентность, если ее не было с самого начала. Если осуществление последовательности измерений квантовой системы меняет ее будущее поведение, то истории, соответствующие возможным последовательностям результатов измерений, являются когерентными. Если последовательность измерений не оказывает влияния на будущее поведение системы, то истории декогерентны. В двухщелевом эксперименте измерение нарушает интерференционную картину и изменяет поведение системы: истории двухщелевого эксперимента, таким образом, являются когерентными.

 

Многомировая интерпретация

 

Идея декогерентных историй в квантовой механике дает интуитивно удовлетворительное решение проблемы измерения. Во время измерения частица и датчик становятся запутанными, и волновая функция является суперпозицией двух состояний. Одно из этих состояний соответствует тому, что «происходит на самом деле». До тех пор пока будущая история частицы и датчика (а также кота, меня и вас) является декогерентной, другое состояние не оказывает никакого дальнейшего влияния.

Другое состояние – другая часть волновой функции – в каком-то смысле все еще присутствует, хотя мы вполне можем его проигнорировать. Эта особенность побудила некоторых ученых предложить так называемую многомировую интерпретацию квантовой механики, согласно которой эта другая часть волновой функции соответствует другому миру, в котором кот жив и здоров. Сторонники многомировой интерпретации говорят, что кот действительно и жив, и мертв в одно и то же время.

В физическом сообществе нет согласия касательно многомировой интерпретации квантовой механики. В 1997 г. я обсуждал эту проблему с физиком из Оксфорда Дэвидом Дойчем, ярым сторонником многомировой картины. Я не уверен, кто вышел победителем в споре, – по крайней мере, в этом мире[36]. В последующих разделах книги я буду использовать «многоисторийную» интерпретацию квантовой механики, предложенную Гелл-Манном и Хартлом. В этой интерпретации квантовая механика поддерживает наборы декогерентных историй так, как описано выше. В реальности реализуется только одна история из этого набора. Остальные истории соответствуют недоступным частям волновой функции. Эти истории соответствуют возможным событиям, которые на самом деле не произошли. (Или, как сказал бы Дэвид Дойч, не произошли в этом мире.)

На мой взгляд, многомировая интерпретация не вполне честно используют выражение «на самом деле». Обычно люди используют фразу «на самом деле», чтобы описать то, что происходит в реальности: я на самом деле написал эти слова, и вы на самом деле их читаете. Есть другие части волновой функции, где я написал что-то другое, а вы смотрите телевизор. Но эти части волновой функции не соответствуют тому, что произошло на самом деле. Они похожи на расходящиеся тропки из рассказа Борхеса: даже если они и существуют, то не оказывают никакого влияния на реальность.

 

 

Глава 6

Атомы за работой

 

Разговаривая с атомами

 

В Нью-Йорке полно людей, которые бродят по улицам и разговаривают сами с собой. Если их спросить, что они делают, они скажут, что общаются с голосами, которых кроме них никто не слышит. Однажды утром, когда я учился в Нью-Йорке, я завтракал у стойки в польском кафе рядом с моей квартирой на углу Второй стрит и авеню B. Я только приступил к своей яичнице с польской колбасой, как вдруг сидевший рядом человек схватил меня за руку, пристально посмотрел мне в глаза и произнес: «Они взяли мозг Эйнштейна и пересадили его в мою голову».

«Серьезно? – отозвался я. – Тогда у меня к вам есть несколько вопросов». И я начал спрашивать, что он думает о квантовой механике и общей теории относительности. К сожалению, судя по его ответам, пересадка мозга прошла не слишком удачно.

Эйнштейн с подозрением относился к квантовой механике. Как мы уже говорили, он никогда не принял до конца эту теорию и не доверял ей. Его не устраивала присущая ей неопределенность. Квантовая механика противоречила его мощной интуиции, впрочем, как и интуиции подавляющего большинства других людей, а Эйнштейн уж точно имел право доверять своим инстинктам. Но здесь интуиция подвела Эйнштейна. Да, квантовая механика вероятностна по своей природе, но ее истинность подтверждают буквально миллионы научных экспериментов.

Чтобы увидеть, как квантовая механика вводит во Вселенную вероятность, полезно рассмотреть простой пример: квантовую игру в кости. (Я давно работаю «атомным массажистом», и у меня есть некоторая практика в квантовой игре на деньги.) Итак, возьмем атом. Облучим его лазером. Теперь облучим его другим лазером и посмотрим, излучает ли наш атом свет. Если излучает, назовем это состояние 0. Если не излучает, назовем это состояние 1. Половину времени атом будет излучать свет (0), а половину времени останется темным (1). Так рождается новый бит.

Давайте пристальнее рассмотрим процесс облучения атома: именно он позволяет нам говорить с ними и слышать, что они отвечают. В отличие от нью-йоркских бродяг, атомы дают реальные ответы: они отвечают на наши вопросы, либо излучая свет, либо нет. Чтобы понять, что отвечают атомы, нужно хоть немного знать их язык.

Атому мы кажемся такими же, какой Земля кажется муравью: очень большими. Обычный размер атомов – несколько десятимиллиардных долей метра, ангстрёмов. Это крошечные, упругие сферы, которые удерживаются вместе благодаря электричеству. В атоме есть компактное ядро, состоящее из протонов (заряженных положительно) и нейтронов (у них заряда нет). Почти вся масса атома приходится на ядро. Ядро окружено облаком электронов, массы которых почти в две тысячи раз меньше, чем у протонов или нейтронов. Электроны заряжены отрицательно и поэтому притягиваются к положительно заряженному ядру; в облаке столько же электронов, сколько протонов в ядре, так что атом в целом электрически нейтрален.

Электрическая сила связывает электроны с ядром. Когда атом находится в своем нормальном, основном состоянии, электроны находятся так близко к ядру, как только могут. (Само ядро удерживает вместе так называемое сильное взаимодействие, которое в 1000 раз сильнее электромагнитного.) Да, но что значит «так близко, как только могут»? Почему электроны просто не падают на ядро, ведь классическая механика предсказывает именно такой исход! Если бы классическая механика была точным описанием природы, то атомы могли бы существовать только в течение крошечной доли секунды, прежде чем исчезнуть во вспышке света. Но корректное описание атомов дает не классическая, а квантовая механика. Квантовая механика гарантирует стабильность атомов, а стабильность атомов, в свою очередь, является одним из самых конкретных подтверждений квантовой механики. Без квантовой механики жизнь атома была бы яркой, но короткой.

Но как квантовая механика обеспечивает стабильность атомов? Мы помним, что каждый электрон имеет свою волну, связанную с его положением и скоростью. Те места, где волна электрона сильна, являются местами наиболее вероятного местонахождения электрона[37]. Чем короче длина волны, тем быстрее движется электрон. Наконец, скорость, с которой волна колеблется вверх и вниз, пропорциональна энергии электрона.

Предположим, что мы хотим разместить волну электрона вокруг ядра атома. Самая простая волна, для которой это можно сделать, – это сфера: волна аккуратно огибает ядро. У следующей по простоте волны есть один пик, когда она огибает ядро; за ней идет волна с двумя пиками, и т. д. Каждый из этих типов волн соответствует электрону в определенном энергетическом состоянии. Самая простая волна – сферическая, без пиков; в этом состоянии у электрона меньше всего энергии. Вторая волна имеет изгибы, а у ее электрона больше энергии. Чем больше пиков в волне электрона, тем быстрее он колеблется и тем больше у него энергии.

Обвяжите камень резиновой лентой и раскрутите его над головой. Чем быстрее движется камень, тем больше у него энергии и тем дальше от вашей головы он обращается, потому что резинка растягивается, чтобы компенсировать дополнительную скорость камня. То же самое верно и для электрона: чем больше его энергия, тем дальше от ядра он обращается. Электрон может подойти ближе всего к ядру, когда у него меньше всего энергии, то есть когда его волна простая, сферическая. Корпускулярно-волновой дуализм подразумевает, что электроны атома состоят из набора дискретных волн, а поэтому и набор орбит у них тоже дискретный. Электроны никогда не падают на ядро, а мы можем подсчитать все возможные варианты (нет пиков, один пик, два пика и т. д.).

Когда электрон переходит из состояния с большей энергией в состояние с меньшей, он испускает квант света – фотон. Энергия фотона равна разности между энергиями этих двух состояний. Разные атомы, например атом фосфора, у которого 15 электронов, или атом железа, у которого их двадцать шесть, испускают фотоны, обладающие разными характерными энергиями. Благодаря соответствию между энергией и скоростью, с которой испускаемые фотоны колеблются вверх и вниз, эти фотоны соответствуют свету той или иной конкретной частоты. Набор таких частот называют спектром атома.

То, что атомы излучают свет с характерным спектром, было замечено еще в первой половине XIX в. Классические физики того времени еще не знали о квантах или фотонах и не могли объяснить эти спектры. Объяснение атомных спектров стало первым великим триумфом квантовой механики. Используя простые отношения между длиной волны и скоростью электронов, а также между частотой, с которой колеблется волна, и ее энергией, Нильс Бор смог вычислить спектр атома водорода и показал, что данная квантово-механическая модель хорошо согласуется с результатами экспериментов.

Атомы могут не только излучать свет, но и поглощать его. Точно так же как атом может перейти из состояния с высокой энергией в состояние с более низкой энергией, испуская в этом процессе фотон, атом может поглотить фотон и перепрыгнуть из состояния с низкой энергией в состояние с более высокой энергией. Возьмем атом в его нормальном состоянии и искупаем его в луче лазерного света, состоящего из фотонов, энергия которых равна разности энергии между нормальным состоянием и следующим по уровню энергии состоянием (оно называется первым «возбужденным состоянием» атома). Атом поглотит один фотон из нашего луча и перейдет из нормального в первое возбужденное состояние.

Если атом искупать в фотонах, энергия которых не равна разности энергий между состоянием, в котором он находится, и каким-то из более энергичных состояний, он не будет поглощать фотоны. Атомы могут поглощать энергию только определенными порциями. Это их качество полезно для управления состоянием атомов. Если атом купается в фотонах неподходящей энергии, он отказывается поглощать ее фотоны и не меняется, а если атом купается в фотонах, энергия которых равна разности энергий его текущего состояния и состояния с более высокой энергией, атом с удовольствием поглотит фотон и перейдет в это состояние. Как мы дальше увидим, тот факт, что атомы реагируют на свет только тех частот, которые соответствует их спектру, весьма полезен, если мы хотим отправить инструкции атомам одного определенного вида, но не других видов.

Переход из одного состояния в другое с испусканием или поглощением фотона требует определенного количества времени, которое зависит от интенсивности лазерного луча. В частности, можно подвергнуть атом воздействию импульса лазерного света со следующим результатом: если атом находится в нормальном состоянии, он переходит в первое возбужденное состояние, поглощая в этом процессе фотон; а если атом находится в первом возбужденном состоянии, он переходит в нормальное состояние, испуская фотон. Нормальное и первое возбужденное состояния атома соответствуют одному биту. Можно принять, что нормальное состояние соответствует 0, а первое возбужденное состояние соответствует 1. Но атом – это не просто бит; это – кубит. Состояния атома соответствуют волнам, точно так же как состояния ядерных спинов, описанных выше. Так что в соответствии с нашим соглашением – заключать квантово-механические объекты в скобки – мы назовем нормальное состояние |0>, а первое возбужденное состояние |1>. Если мы применим к атому лазерный импульс, |0> перейдет в |1>, а |1> перейдет в |0>. На языке атомов – атом просто переходит из состояния в состояние; на языке нулей и единиц – это уже известная нам логическая операция «не». Говоря на языке атомов, мы можем заставить атом инвертировать бит.

Как заставить атом отвечать нам? Мы можем воздействовать на атом светом, и атом ответит нам, тоже используя свет. Представим себе третье состояние, |2>, с более высокой энергией, чем в состояниях кубита |0> и |1>. Предположим, что всякий раз, когда атом находится в состоянии |2>, он имеет тенденцию спонтанно возвращаться в |0>, в нормальное состояние, испуская при этом фотон. Спонтанное излучение ответственно за явление флуоресценции. Флуоресцентная лампа возбуждает атомы из их нормального состояния и позволяет им переходить обратно, излучая свет. Энергия испускаемого фотона равна разности энергий между состоянием |2> и состоянием |0>. Если посмотреть внимательно, скажем в микроскоп, иногда можно увидеть испускаемый фотон как вспышку света. Это атом говорит с нами.

 

 

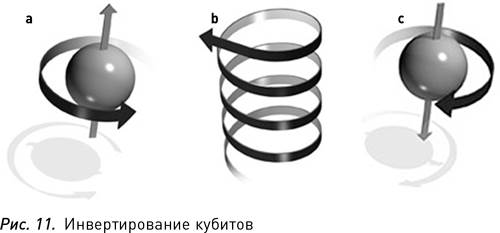
Историю Вселенной можно рассматривать как последовательность революций в сфере обработки информации, каждая из которых основана на технологиях, возникших в результате предыдущих революций

Чтобы инвертировать квантовый бит, достаточно просто направить на него луч света. Рис. 11a показывает кубит – ядерный спин – в состоянии «вверх», или 0. На рис. 11b появляется частица света, или фотон. Она поглощается ядерным спином, который переходит в состояние «вниз», или 1 (рис. 11c)

 

Способность видеть спонтанно испускаемые фотоны позволяет нам определить, находится ли атом в нормальном состоянии. Искупайте атом в свете из фотонов, энергия каждого из которых равна разности энергий между состояниями |0> и |2>. Если атом находится в нормальном состоянии, то, поскольку фотоны, в которых он купается, обладают правильной энергией, он поглотит фотон и перейдет в состояние |2>. Вскоре после этого он испустит фотон и вернется в нормальное состояние. Затем он поглотит еще один фотон и перейдет в состояние |2>. Затем он испустит фотон и опять вернется в нормальное состояние. Такой процесс, в котором атом продолжает поглощать и испускать фотоны, называют «циклическим переходом», потому что атом переходит туда и обратно между двумя хорошо определенными состояниями.

Если же атом сначала находится в состоянии |1>, то он не может поглотить фотон и перейти в состояние |2>, потому что доступные ему фотоны обладают неподходящей энергией. Атом, который сначала находится в состоянии |1>, в нем и останется, не обращая внимания на фотонный душ, и флуоресценции не будет. А вот атом, который демонстрирует флуоресценцию, по существу, говорит нам: «Я – 0! Я – 0! Я – 0! Я – 0!»

Теперь давайте посмотрим повнимательнее, как атомы переходят из одного состояния в другое под воздействием лазера. Возьмем атом в его нормальном состоянии и искупаем его в свете из фотонов, энергия которых равна разности энергий нормального и первого возбужденного состояния. Что происходит во время скачка? Во время перехода атом и свет находятся в состоянии, которое является суперпозицией нормального состояния атома без поглощенного фотона, и атома в первом возбужденном состоянии с одним поглощенным фотоном. То есть состояние атома – суперпозиция двух волн. Первая волна находится в нормальном состоянии, а вторая волна – в первом возбужденном состоянии. Сразу же после того как атом начинает принимать световой душ и начинает переход, эта суперпозиция состоит главным образом из нормального состояния с небольшой «примесью» возбужденного. В середине перехода атом и световая ванна находятся в примерно равной суперпозиции состояний |0, фотон не поглощен> + |1, фотон поглощен>. Вблизи конца перехода суперпозиция представляет собой главным образом возбужденное состояние, с небольшим остатком нормального состояния.

Итак, атом перескакивает из нормального состояния в возбужденное не сразу. Он скорее «скользит» через непрерывную последовательность промежуточных суперпозиций. Такое же непрерывное скольжение происходит, когда атом возвращается из первого возбужденного в нормальное состояние, испуская фотон. Атом и фотонный душ начинают в состоянии |1, фотон не испущен>, и заканчивают в состоянии |0, фотон испущен>. В середине перехода атом и душ находятся в состоянии суперпозиции |1, фотон не испущен> + |0, фотон испущен>.

Такое описание атома, переходящего из одного состояния в другое с поглощением или испусканием фотона, похоже на сделанное ранее описание ядерного спина, переходящего из одного состояния в другое под воздействием магнитного поля. Действительно, эти два процесса по сути одинаковы. Поворачиваясь, ядерный спин также поглощает фотон – из магнитного поля – и испускает фотон, возвращаясь в исходное состояние.

Теперь вы знаете, как разговаривать с атомами. Облучая атом лазером, можно управлять его состоянием. Можно непрерывно проводить атом через последовательность состояний суперпозиции; можно возбудить его, заставляя поглотить фотон, и вернуть обратно из возбужденного состояния, заставляя испустить фотон. Мы также знаем, как заставить атом нам отвечать. Управляя циклическими переходами, можно спросить атом, содержит ли он 0 или 1, и получить ответ. Все это значит, что теперь мы получили возможность создавать новые биты.

Возьмем атом и подействуем на него лазером, чтобы перевести в суперпозицию |0> + |1>. Теперь запустим циклический переход, чтобы увидеть, находится ли атом в состоянии 0 или в состоянии 1. Если состояние атома 0, он будет флуоресцировать; если его состояние 1, он останется темным. Мы подбросили квантовую монетку и создали совершенно новый бит.

Разговор с атомом посредством циклического перехода измеряет состояние атома и создает информацию. Конечно, как и в предыдущей главе, то, что происходит во время измерения, открыто для интерпретации. Если рассматривать измерения как коллапс волновой функции, волновая функция атома, взятого вместе с фотонами, коллапсирует либо до состояния |0, есть флуоресценция>, либо до состояния |1, нет флуоресценции>.

В интерпретации декогерентных историй состояние атома вместе с фотонами находится в суперпозиции |0, есть флуоресценция> + |1, нет флуоресценции>. Каждое из состояний в этой суперпозиции соответствует декогерентной истории. В нашем случае истории чрезвычайно декогерентны. Чтобы сделать их когерентными, нужно было бы собрать все фотоны, испущенные атомом, отразить их назад и заставить атом повторно их поглотить. Для этого нужен своего рода демон Лошмидта, способный изменять последовательность событий во времени. Но обратить фотоны, рассеянные по всей Вселенной, трудно (если вы сомневаетесь – валяйте, обратите их!). Из-за того что два состояния в суперпозиции декогерентны, атом и фотон ведут себя так, как будто они находятся или в одном состоянии, или в другом, и мы действительно создаем совершенно новый бит, никогда не существовавший прежде.

 

Квантовые вычисления

 

Если облучить атом светом, фотоны которого обладают подходящей энергией, можно заставить атом изменить состояние из |0> в |1> и обратно. Так мы инвертируем бит атома. Другими словами, мы выполняем логическую операцию «не». В статье «Потенциально реализуемый квантовый компьютер» (A Potentially Realizable Quantum Computer), опубликованной в 1993 г. в журнале Science, я показал, что немного более сложный набор последовательностей лазерных импульсов, чем используемый для операции «не», позволяет атомам выполнять логические операции «и», «или» и «копировать» – точно так же, как в обычных цифровых вычислениях. Каждый атом хранит один бит, и набор атомов может вычислять все, что может вычислять обычный PC или Mac.

Но атомы могут сделать намного больше, чем обычный PC или Mac. Атомы могут хранить нечто большее, чем биты; они могут хранить кубиты. В отличие от классических битов, кубиты могут находиться в квантовых суперпозициях |0> и |1>, то есть они могут быть в состоянии 0 и 1 в одно и то же время. Можно ли каким-то образом использовать эти квантовые суперпозиции для вычислений, которые не могут делать классические компьютеры? Этот вопрос впервые поднял Дэвид Дойч в середине 1980-х гг., но ответ на него был найден только в начале 1990-х. И этот ответ – да.

Чтобы увидеть, почему квантовые компьютеры и квантовые биты могут сделать больше, чем классические компьютеры и классические биты, давайте вспомним, что делают биты в компьютере. Некоторые из них, например биты на жестком диске компьютера или в его памяти, просто хранят информацию. Например, биты в памяти моего компьютера получают и хранят этот текст, по мере того как я его печатаю. Другие биты, например биты компьютерных программ, являются инструкциями или командами. Они велят компьютеру делать то или другое. Функционирует ли бит как бит памяти или как бит команды, зависит от контекста, в котором он используется.

Рассмотрим бит, который компьютер интерпретирует как команду: 0 означает «Делай это!», а 1 означает «Делай то!» «Это» может быть, скажем, «прибавь 2 к 2», а «то» может быть «прибавь 3 к 1». Или «это» может означать «отправь электронное письмо», а «то» – «открой веб-браузер».

В отличие от классического бита, квантовый бит может содержать 0 и 1 в одно и то же время. Что делает квантовый компьютер, когда он пытается интерпретировать такой кубит как команду? Часть суперпозиции, обозначаемая нулем, говорит квантовому компьютеру: «Делай это», а часть суперпозиции, соответствующая единице, говорит: «Делай то». Как же квантовый компьютер решает, что ему делать? А никак! Он делает «то» и «это» одновременно! Как квантовый бит может хранить два значения сразу, так и квантовый компьютер может выполнять два вычисления одновременно.

Дэвид Дойч назвал эту парадоксальную способность квантового компьютера делать две вещи сразу «квантовым параллелизмом». Квантовый параллелизм очень отличается от обычных классических параллельных вычислений. Классический параллельный компьютер состоит из нескольких процессоров, соединенных вместе. При классическом параллельном вычислении один процессор выполняет одну задачу, а другие процессоры выполняют другие задачи. В случае квантового параллелизма один квантовый процессор выполняет несколько задач сразу.

Эта способность делать две вещи сразу присуща именно квантовой механике. В двухщелевом эксперименте фотон может пройти через обе щели сразу; кубит может хранить 0 и 1 в одно и то же время; квантовый компьютер может выполнять две разных задачи одновременно. Способность делать две вещи сразу является результатом волновой природы квантовой механики. Каждое возможное состояние квантовой системы соответствует волне, а волны могут накладываться друг на друга.

Мы все знакомы с ситуациями, где наложение волн приводит к качественно новым и более богатым явлениям. Рассмотрим звуковые волны. Волна, колеблющаяся вверх и вниз на определенной частоте, соответствует чистому тону. Звуковая волна, колеблющаяся вверх и вниз 440 раз в секунду, соответствует звуку ноты «ля» первой октавы. Звуковая волна, колеблющаяся вверх и вниз 330 раз в секунду, дает звук ноты «ми» первой октавы. Суперпозиция этих двух волн соответствует аккорду, который обладает качественно иным, более богатым звуком, чем звук любого чистого тона, взятого отдельно. Богатство звука возникает благодаря интерференции, наложению этих двух чистых тонов.

Классическое вычисление похоже на сольную партию – отдельные строки чистых тонов, следующие друг за другом. Квантовое вычисление похоже на симфонию, состоящую из множества строк тонов, интерферирующих друг с другом. Именно это явление интерференции придает квантовому вычислению его особые качества и дополнительную мощь.

Квантовые вычисления не ограничиваются всего двумя «партиями». Как и симфония, квантовое вычисление становится богаче и сильнее, создавая сложные последовательности аккордов. Например, предположим, что на вход компьютера подается «кутрит» с тремя возможными состояниями: 0, 1 и 2. Состояние 0 инструктирует квантовый компьютер «делать это», состояние 1 инструктирует его «делать то», а состояние 2 инструктирует его «делать что-то еще». Если «это» означает «прибавить 2 к 2», а «то» означает «прибавить 3 к 1», то «что-то другое» может означать «прибавить 4 к 0». Когда квантовому компьютеру на вход подают суперпозицию всех трех инструкций, он начинает делать «это», «то» и «что-то другое» сразу. В нашем примере компьютер одновременно исследует все возможные способы получить 4 как сумму неотрицательных целых чисел. Такое квантовое вычисление похоже на трио, где три волны интерферируют, накладываются друг на друга, а три вычисляющих «голоса» сотрудничают над разложением числа 4 на слагаемые и делают это быстрее, чем мог бы сделать один вычисляющий «голос».

Количество вещей, которые одновременно может делать квантовый компьютер – число голосов в симфонии квантового вычисления – быстро растет с увеличением числа входных битов. Даже небольшое количество кубитов может создать чрезвычайно богатую фактуру интерферирующих волн в ходе вычисления. Квантовый компьютер, получивший на входе 10 кубитов, может делать 1024 (210) вещей сразу. Квантовый компьютер, получивший 20 кубитов, может сделать 1 048 576 (220) вещей сразу. При 300 кубитах на входе он может одновременно сделать больше вещей, чем элементарных частиц во всей Вселенной. Квантовый параллелизм позволяет даже относительно маленькому квантовому компьютеру, содержащему всего несколько сотен кубитов, одновременно исследовать огромное количество возможностей.

 

И снова проблема измерения

 

Но что происходит, когда мы берем квантовый компьютер, делающий несколько вещей сразу, и спрашиваем его, что он делает? Возможно ли провести измерения, чтобы определить, делает ли он «это», «то» или «что-то другое»? Как и с любой квантовой системой, когда мы проводим измерения в суперпозиции нескольких возможных состояний, результат измерения дает случайным образом одну из этих возможностей. Так, если квантовый компьютер исследует все способы получить цифру 4 как сумму положительных целых чисел, то когда мы начнем его опрашивать, он скажет, например: «О, я прибавляю 3 к 1», или: «Я прибавляю 2 к 2».

Следуя метафоре квантового вычисления как симфонии: если мы измеряем квантовый компьютер, в то время как он вычисляет, мы не слышим всего оркестра; мы слышим только один голос, выбранный случайным образом.

Вспомним двухщелевой эксперимент. В этой модели электрон делает две вещи сразу: он проходит через обе щели одновременно. Когда мы проводим измерения, чтобы выяснить, через какую щель проходит электрон, он обнаружится в одной или во второй щели, случайным образом. Точно так же, если мы возьмем квантовый компьютер, делающий две вещи сразу, и измерим его, чтобы выяснить, что он делает, то окажется, что он делает одну или другую из этих вещей, случайным образом. Если мы хотим увидеть интерференционную картину в эксперименте с двойной щелью, нам нужно подождать, пока электрон достигнет экрана, чтобы две волны – одна от одной щели, вторая от другой – смогли проинтерферировать друг с другом. Картина интерференции возникает из «дуэта» этих двух волн. В квантовом вычислении, если мы хотим получить от него максимальную пользу, не следует наблюдать за вычислением, когда оно происходит. Чтобы получить полный симфонический эффект квантов