
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Момент сил, действующих на виток с током в магнитном полеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле
Рис.3.15 Принцип суперпозиции магнитных полей
Каждый ток создает свое магнитное поле независимо от других токов и вектора Индукция результирующего магнитного поля от сложения магнитных полей:
Закон Био-Савара-Лапласа и его применение к расчету магнитных полей
Этот закон позволяет определить величину вектора магнитной индукции
или
т.е. индукция dВ магнитного поля, созданная бесконечно малым элементом dℓ проводника с током I в точке поля на расстоянии r от элемента до этой точки, прямопропорциональна силе тока I длине элемента dℓ и обратно пропорциональна r2 от элемента до точки – это и есть закон Био-Савара-Лапласа (рис.3.16).
Рис.3.16 Угол α в формуле (3.59) это угол между направлением тока и вектором-радиусом Пример: определим магнитную индукцию в центре кругового тока I радиусом R (рис.3.17)
Рис.3.17
с учетом того, что в формуле (3.59) r = R, α = 900. Аналогичным образом, интегрируя уравнение (3.59) с учетом формы проводника, получаем: а) для бесконечно длинного прямого тока:
где r- кратчайшее расстояние от оси провода до точки, в которой определяется магнитная индукция; б) для отрезка проводника с током I:
где α1 и α2-углы между радиусами-векторами, проведенными в данную точку поля соответственно из начала и конца проводника, и направлением тока; в) закон полного тока проводимости:
где ℓ -длина произвольного замкнутого контура в магнитном поле; n -число витков, охватываемых контуром. Пользуясь законом полного тока, рассчитаем напряженность Н и индукцию
С другой стороны
Напряженность магнитного поля вне бесконечного длинного соленоида считаем равной нулю. Поле внутри длинного соленоида однородно. Для магнитной индукции поля соленоида имеем:
Формулы (3.64) и (3.65) справедливы и для тороида (кольцевого соленоида радиуса R, где ℓ=2πR). Рис. 3.18
Рис.3.18
|
||||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 1780; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 или
или  (3.58)
(3.58) α - угол между векторами
α - угол между векторами  (направлен по нормали к контуру) и
(направлен по нормали к контуру) и  (рис.3.15)
(рис.3.15) ) этих полей складываются геометрически (принцип суперпозиции).
) этих полей складываются геометрически (принцип суперпозиции). ;
; 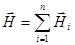 .
. ) в любой точке поля на расстоянии r от проводника с током I. Так как форма проводника может быть разной, то выделяется на проводнике элемент dℓ его длины столь малый, что можно пренебречь его кривизной, и тогда в векторном виде:
) в любой точке поля на расстоянии r от проводника с током I. Так как форма проводника может быть разной, то выделяется на проводнике элемент dℓ его длины столь малый, что можно пренебречь его кривизной, и тогда в векторном виде:
 (3.59)
(3.59)

 .
.
 (3.60)
(3.60) или
или  (3.61)
(3.61) , (3.62)
, (3.62) или
или 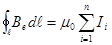 (3.63)
(3.63)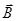 магнитного поля тороида и соленоида. Пусть соленоид имеет N витков с током I и длину L. Проведем замкнутый контур ℓ через середину соленоида так, чтобы он охватывал все витки. Тогда алгебраическая сумма всех охватываемых контуром токов будет:
магнитного поля тороида и соленоида. Пусть соленоид имеет N витков с током I и длину L. Проведем замкнутый контур ℓ через середину соленоида так, чтобы он охватывал все витки. Тогда алгебраическая сумма всех охватываемых контуром токов будет:
 . Приравняв, получим:
. Приравняв, получим: или
или  , (3.64)
, (3.64) (3.65)
(3.65)



