
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Внутренняя энергия идеального газа. РаботаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Термодинамика в отличие от молекулярно-кинетической теории, изучает физические свойства макроскопических тел (термодинамических систем), не вникая в их молекулярное строение. Термодинамический метод базируется на законе сохранения и превращении энергии. Физические величины, характеризующие термодинамическую систему, называются термодинамическими параметрами. К ним относятся: объем, давление, температура, концентрация и др. Любое изменение в термодинамической системе, связанное с изменением ее параметров, называется термодинамическим процессом, а уравнение, связывающее между собой параметры системы, называется уравнением состояния. Примером такого уравнения является уравнение Менделеева - Клапейрона (6.1)
Внутренняя энергия идеального газа Важнейшей характеристикой термодинамической системы является ее внутренняя энергия U, складывающая из потенциальной энергии взаимодействия частиц системы и кинетической энергии их теплового движения. Внутренняя энергия является функцией состояния системы, т.е. в каждом состоянии система обладает вполне определенным значением внутренней энергии, не зависящим от того, каким путем система перешла в это состояние. Так как в идеальном газе потенциальная энергия молекул равна нулю (считается, что молекулы между собой не взаимодействуют), то внутренняя энергия идеального газа равна полной кинетической энергии всех его молекул. Обозначив внутреннюю энергию одного моля газа через Uμ, а среднюю кинетическую энергию молекулы через Uμ = NA где NA – число Авогадро. Подставляя значение
Если число молей
Следовательно, внутренняя энергия газа пропорциональна его массе, числу степеней свободы молекулы и абсолютной температуре газа.
Первый закон термодинамики Внутреннюю энергию термодинамической системы можно изменить за счет работы, которую либо внешние тела совершают над ней, либо сама система совершает над внешними телами. Например, приложив внешнюю силу, мы сжимаем газ, в результате чего его температура повышается, а, следовательно, увеличивается и внутренняя энергия. Внутреннюю энергию можно изменить также, передавая системе (или отнимая у нее) некоторое количество теплоты. Согласно закону сохранения энергии, изменение внутренней энергии системы должно равняться сумме полученной ею теплоты и совершенной над ней работы. Эта формулировка закона сохранения энергии применительно к термодинамическим системам носит название первого закона термодинамики: ΔU = Q – A или Q = ΔU + A (6.21) Условимся считать, что теплота положительна Q>0 тогда, когда она сообщается системе, а работа положительна, когда система совершает ее над внешними телами. В дифференциальной форме первый закон термодинамики имеет вид: dQ = dU + dA Необходимо подчеркнуть, что в отличие от внутренней энергии, являющейся функцией состояния, работа и количество теплоты зависят не только от начального и конечного состояний системы, но и от пути, по которому происходило изменение ее состояния. Следовательно, величины dQ и dА не являются полными дифференциалами, по которым может производиться интегрирование. Для того, чтобы подчеркнуть это обстоятельство для бесконечно малых приращений тепла и работы применяют более корректное обозначение Найдем в общем виде работу, совершаемую газом, (рис.6.6, а). Если газ, расширяясь, перемещает поршень на расстояние dx, то он производит работу (см. формулу 2.19):
Рис.6.6
где S – площадь поршня; Sdx = dV – изменение объема газа в цилиндре. Полная работа, совершаемая газом при изменении его объема от V1 до V2, равна:
Графически процесс изменения состояния газа при его расширении изображается участком кривой 1-2 в координатах Р – V (рис.6.6, б). Точки 1 и 2 соответствуют начальному и конечному состояниям газа. Элементарная работа PdV изображается заштрихованной площадью. Полная работа, определяемая формулой 6.23, изображается площадью V1 – 1 – 2 - V2 под кривой 1 – 2. Теплоемкость идеальных газов. Количество тепла, которое надо сообщить телу, чтобы изменить его температуру на 1 К, называется теплоемкостью тела С. Согласно этому определению
Теплоемкость единицы массы вещества называется удельной теплоемкостью Суд
Теплоемкость одного моля называется молярной теплоемкостью См.
где ν = m/μ – число молей. Как следует из формул (6.25) и (6.26), удельная теплоемкость связана с молярной соотношением: См = Суд · μ (6.27) Теплоемкость газа зависит от того, при каких условиях она определяется: при постоянном объеме или постоянном давлении. Покажем это, для чего запишем первый закон термодинамики с учетом формулы (6.22): δQ = dU + PdV (6.28) Если газ нагревается при постоянном объеме (изохорный процесс), то dV=0 и работа РdV = 0. В этом случае δQ = dU, т.е. передаваемое газу тепло идет только на изменение его внутренней энергии. Теплоемкость газа при постоянном объеме:
С учетом формулы (6.20)
и тогда изохорная теплоемкость
Для одного моля (m/µ = 1) молярная теплоемкость при постоянном объеме
Теперь, с учетом равенства (6.28), найдем теплоемкость при постоянном давлении (изобарный процесс):
(при этом учли, что dU/dT = CV). Из (6.32) следует, что СP > CV. Это объясняется тем, что при нагревании при P = const сообщенное газу тепло идет не только на увеличение его внутренней энергии, но и на совершение работы. Для одного моля идеального газа уравнение Менделеева – Клапейрона имеет вид PV=RT и потоку PdV=RdT. Учитывая это, получим уравнение Майера, выражающее связь между молярными теплоемкостями при постоянном давлении и постоянном объеме: Смр = Сmv + R (6.33) Учитывая выражение (6.31) можно записать в виде
При рассмотрении термодинамических процессов важно знать характерное для каждого газа отношение СP к СV:
Величина γ называется коэффициентом Пуассона, i – число степеней свободы молекул (см. рис.6.2). Повышение температуры приводит, как отмечалось выше, к появлению колебательных степеней свободы, в результате чего теплоемкость возрастает. Наоборот, при низких температурах число степеней свободы уменьшается, так как «вымораживаются» вращательные степени свободы и теплоемкость газа уменьшается. Изопроцессы
Изопроцессом называется процесс, при котором один из параметров термодинамической системы остается постоянным. Связь между параметрами системы дает уравнение Менделеева – Клапейрона.
Изотермический процесс (Т = const).
В этом случае уравнение состояния имеет вид: PV = const (6.36) Для нескольких конкретных состояний газа можно записать: P1V1 = P2V3 =..., = PnVn График изотермического процесса (изотерма) в координатах P – V изображается гиперболой (рис.6.7). Подставляя
Работа изотермического процесса на рис.6.7 численно равна площади под кривой 1-2. Из формулы 6.29 следует, что изменение внутренней энергии при dT = 0 в изотермическом процессе равно 0. Тогда первый закон термодинамики применительно к изотермическому процессу примет вид Q = A
Рис.6.7
т.е. система: либо, получая тепло от внешней среды, совершает работу, расширяясь, либо отдает тепло внешней среде вследствие того, что внешние тела совершают над ней работу, сжимая ее. Следовательно, для того, чтобы при изотермическом расширении температура не падала, к газу необходимо подводить количество теплоты, эквивалентное работе расширения. Наоборот, при сжатии система должна отдавать среде количество теплоты, эквивалентное работе сжатия. Изобарный процесс (Р = const). Уравнение состояния при Р = const имеет вид
График изобарного процесса в координатах Р – V приведен на рис.6.7. Работа при изобарном процессе (см.6.23)
на графике работа при Р = const численно равна площади прямоугольника под прямой 1-3. Первый закон термодинамики для изобарного процесса Q = ΔU + A Изохорный процесс (V = const). При изохорном процессе уравнение состояния
Поскольку dV = 0, то работа при изохорном процессе равна нулю. Первый закон термодинамики для изохорного процесса имеет вид Q = ΔU, т.е. либо вся теплота, сообщаемая системе, идет на увеличение ее внутренней энергии, либо система отдает среде тепло, уменьшая свою внутреннюю энергию. Адиабатический процесс. Адиабатическим называется процесс, протекающий без теплообмена с внешней средой(δQ = 0). Близким к адиабатическим являются все быстропротекающие процессы, например, расширение и сжатие горючей смеси в двигателях внутреннего сгорания. Учитывая, что δQ = 0, запишем первый закон термодинамики для адиабатического процесса: А = -ΔU (6.41) Отсюда следует, что если газ совершает работу (адиабатически расширяясь), то А>0, соответственно ΔU<0 и ΔТ<0, т.е. газ охлаждается. Наоборот, при адиабатическом сжатиии газа А<0, тогда ΔU >0 и ΔТ >0, т.е. газ нагревается. Используя выражение (6.23) и учитывая, (6.20), перепишем равенство (6.41):
Продифференцируем уравнение Менделеева – Клапейрона (6.1):
Исключив из уравнений (6.42) и (6.43) температуру Т, получим
или
Разделив переменные и учитывая равенство (6.35), найдем
Интегрируя это равенство, получим γlnV + lnP = const Или в окончательном виде связь между давлением и объемом газа в адиабатическом процессе: PVγ = const (6.44) Это отношение называется уравнением адиабаты или уравнением Пуассона. Кривая адиабаты представлена на рис.6.7, которая падает с ростом объема круче, чем изотерма. Это непосредственно следует из того, что γ>1 (см. также формулу 6.35). Уравнение Пуассона можно выразить и через другие параметры с помощью уравнения Менделеева – Клапейрона TVγ-1 = const Tγ P1-γ = const Вычислим работу расширения газа в адиабатическом процессе. Учитывая равенство (6.42), получим
|
||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 3363; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

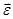 , можем записать для одного моля газа:
, можем записать для одного моля газа: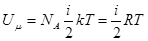 (6.19)
(6.19)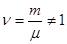 , то для любого количества вещества
, то для любого количества вещества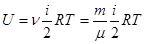 (6.20)
(6.20)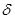 Q и
Q и 
 или
или  (6.23)
(6.23)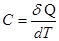 , [С] = Дж/К (6.24)
, [С] = Дж/К (6.24)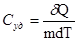
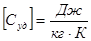 (6.25)
(6.25)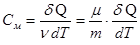 , [См] = Дж/моль · К (6.26)
, [См] = Дж/моль · К (6.26)
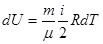 (6.29)
(6.29) (6.30)
(6.30)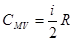 (6.31)
(6.31) (6.32)
(6.32) (6.34)
(6.34) (6.35)
(6.35)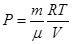 из формулы (6.1) в формулу работы (6.23), получим для изотермического процесса:
из формулы (6.1) в формулу работы (6.23), получим для изотермического процесса: (6.37)
(6.37)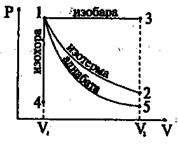 .
.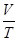 = const или
= const или 
 (6.39)
(6.39)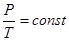 или
или 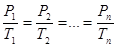 (6.40)
(6.40)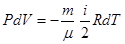 (6.42)
(6.42) (6.43)
(6.43)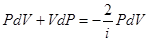
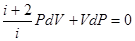
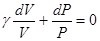
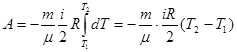 (6.45)
(6.45)


