
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальная форма закона ОмаСодержание книги
Поиск на нашем сайте
Введем понятие плотности тока:
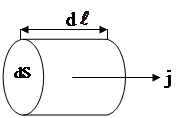
Рис. 3.9
Выразим: dI = jdS,
dU = dφ = Edℓ, (см. 3.22)
dI =
Тогда jdS = dI =
или
где γ=1/ρ- удельная проводимость;
Работа постоянного тока силой I на участке цепи с напряжением U и сопротивлением R за время t:
Полная мощность, развиваемая источником с ЭДС ε: Р=Iε (3.45) Полезная мощность, выделяемая на внешнем сопротивлении R:
КПД источника тока
Сопротивление проводников:
где Ri – сопротивление i-того проводника.
Закон Джоуля-Ленца
При протекании постоянного тока по проводнику в нем выделяется количество тепла Q: Q= I2Rt=UIt (3.48) Когда ток постоянен, а проводник неподвижен, то вся работа сторонних сил расходуется на его нагревание. Если сила тока меняется, то количество тепла dQ, выделившегося на сопротивлении R за время dt при прохождении через него электрического тока: dQ Пусть сила тока I является некоторой функцией времени. В случае:
где k-коэффициент пропорциональности, характеризующий скорость изменения силы тока:
С учетом этого, формула (3.49) примет вид: dQ= (I0 + kt)2 Rdt Для определения тепла, выделившегося за конечный интервал времени Δt, проинтегрируем в пределах от t1 до t2: Q= Если начальный ток I0=0, то: Q= Закон Джоуля-Ленца в дифференциальной форме. В формулу (3.49) подставим R=ρdℓ/dS и j=dI/dS, получим: dQ тогда удельная тепловая мощность тока (в 1м3 в 1с):
ω=γЕ 2 (3.52) Подсчет конечной величины тепла: Q Правила Кирхгофа для разветвленных цепей.
Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю:
При этом токи, подходящие к узлу, считаются положительными, а токи, отходящие от узла, - отрицательными. Второе правило Кирхгофа: в любом замкнутом контуре алгебраическая сумма произведений сил токов на сопротивление соответствующих участков этого контура равна алгебраической сумме ЭДС в контуре.
При этом, если токи по направлению совпадают с выбранным направлением обхода контура, то они считаются положительными, а несовпадающие - отрицательными. ЭДС источника берется со знаком “плюс”, если при выбранном обходе контура осуществляется переход внутри источника от отрицательного полюса к положительному, в противном случае ЭДС берется со знаком “минус”.
Магнитное поле
В 1820 году датский физик Эрстед обнаружил, что протекающий по проводнику ток действует на магнитную стрелку. Опыт показал также, что неподвижные заряды не создают вокруг себя магнитное поле. В отличии от электростатического магнитное поле имеет вихревой характер, т.е. линии этого поля всегда замкнуты (рис.3.10). Направление линий определяется правилом буравчика или правой руки.
Рис.3.10
Основной характеристикой магнитного поля является вектор магнитной индукции Кроме вектора магнитной индукции
где m - магнитная проницаемость среды (для вакуума m=1);
Сила Лоренца действует на заряд Q, движущийся в магнитном поле с индукцией В со скоростью V
где α - угол между векторами Сила Лоренца равна нулю, когда заряд движется вдоль магнитного поля (sinα =0), и максимальна, когда заряд движется перпендикулярно к нему (sinα =1). Направление Fл определяется по правилу левой руки (для положительного заряда). Ладонь располагается так, чтобы линии индукции в нее входили, четыре пальца указывали направление вектора скорости движения заряда. Тогда отставленный большой палец укажет направление действия силы. При движении отрицательного заряда сила направлена в противоположную сторону (рис.3.11).
а) б) Рис.3.11
Пусть положительный заряд Q движется перпендикулярно линиям вектора магнитной индукции Частица в данном случае будет двигаться по окружности в плоскости, перпендикулярной магнитному полю. Радиус R этой окружности найдем из условия, что сила Лоренца является здесь центростремительной силой.
Тогда Далее по формулам V = wR = 2pnR = В общем случае угол α в формуле (3.54) не обязательно равен 900. Тогда заряд будет двигаться в магнитном поле по винтовой линии с периодом Эффект Холла заключается в том, что при протекании тока в проводнике или полупроводнике в них возникает поперечная току разность потенциалов Δφ. Этотакже можно объяснить действием силы Лоренца на подвижные заряды (ток). Рассмотрим пластину с током I, перпендикулярным постоянному магнитному полю с индукцией В (рис.3.12)
Рис. 3.12
Под действием силы Лоренца Fл = QVB происходит разделение зарядов и между поверхностями пластин создается разность потенциалов Δφ. Возникшее электрическое поле действует на заряды с силой
тогда где K -постоянная Холла. Определив K, можно рассчитать концентрацию носителей. Сила Ампера действует на элемент тока dℓ в магнитном поле с индукцией В
где α-угол между вектором Направление силы Ампера F находится по правилу левой руки: вектора
Рис.3.13
Из формулы (3.56) следует, что если F = 1H, I = 1A, ℓ= 1м, то В будет 1 Тл (Тесла)
1Тл = т.е. 1 Тл это индукция такого магнитного поля, которое на проводник длиной 1 м с током в 1 А действует с силой в 1 Н. Магнитный момент контура с током:
где S-площадь контура;
Вектор рm перпендикулярен к площади контура и определяется правилом буравчика, вращаемого по току (рис.3.14)
Рис. 3.14
|
|||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 699; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

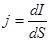 , т.е. j - численно равен току dI через площадь dS, перпендикулярную току. Выделим в проводнике элементарный цилиндр с образующими, параллельными
, т.е. j - численно равен току dI через площадь dS, перпендикулярную току. Выделим в проводнике элементарный цилиндр с образующими, параллельными  .
.
 , (с учетом 3.41) R =
, (с учетом 3.41) R = 
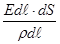
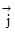 =
= 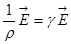 , (3.43)
, (3.43) - вектор напряженности поля.
- вектор напряженности поля.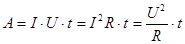 (3.44)
(3.44)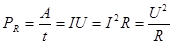 (3.46)
(3.46) (3.47)
(3.47)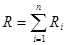 - при последовательном соединении;
- при последовательном соединении; - при параллельном соединении;
- при параллельном соединении; . (3.49)
. (3.49) ,
,
 (3.50)
(3.50) (3.51)
(3.51)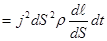 , где dS · dℓ = dV -объем,
, где dS · dℓ = dV -объем,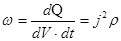 , с учетом формулы (3.43)
, с учетом формулы (3.43)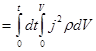
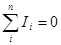


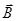 . Он направлен всегда по касательной к линии поля в любой точке.
. Он направлен всегда по касательной к линии поля в любой точке.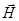
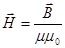 , (3.53)
, (3.53) - магнитная постоянная в СИ системе.
- магнитная постоянная в СИ системе. или Fл = QVB sin α, (3.54)
или Fл = QVB sin α, (3.54)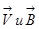 .
.
 перпендикулярен к вектору скорости
перпендикулярен к вектору скорости  и сообщает заряду нормальное ускорение аn, т.е.
и сообщает заряду нормальное ускорение аn, т.е.  , где m – масса частицы с зарядом Q.
, где m – масса частицы с зарядом Q. т.к. an = V2 / R (см.2.12)
т.к. an = V2 / R (см.2.12) .
. можно вычислить угловую скорость w вращения частицы, частоту ее вращения n или период Т.
можно вычислить угловую скорость w вращения частицы, частоту ее вращения n или период Т. и шагом
и шагом  и радиусом
и радиусом 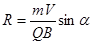 .
.
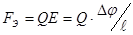 . При равенстве
. При равенстве  разделение зарядов прекращается, при этом Δφ=ℓVB. Ток в пластинке можно выразить через объемную плотность заряда Qn, площадь поперечного сечения ℓd проводника, скорость заряда V, т.е. I= Q nℓdV, откуда:
разделение зарядов прекращается, при этом Δφ=ℓVB. Ток в пластинке можно выразить через объемную плотность заряда Qn, площадь поперечного сечения ℓd проводника, скорость заряда V, т.е. I= Q nℓdV, откуда: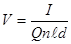
 , (3.55)
, (3.55) или
или  , (3.56)
, (3.56) - в ладонь, четыре пальца – ток, большой палец – сила
- в ладонь, четыре пальца – ток, большой палец – сила  (рис.3.13)
(рис.3.13)
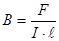 ,
,
 (3.57)
(3.57) -единичный вектор нормали к плоскости контура.
-единичный вектор нормали к плоскости контура.



