
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы механики сплошных средСодержание книги
Поиск на нашем сайте Жидкости и газы во многом схожи по своим свойствам. Они текучи и принимают форму того сосуда, в котором находятся. Они подчиняются законам Паскаля и Архимеда. При рассмотрении движения жидкостей можно пренебречь силами трения между слоями и считать их абсолютно несжимаемыми. Такая абсолютно невязкая и абсолютно несжимаемая жидкость называется идеальной. Движение жидкости можно описать, если показать траектории движения ее частиц таким образом, чтобы касательная в любой точке траектории совпадала с вектором скорости. Эти линии называются линиями тока. Линии тока принято проводить так, чтобы их густота была больше там, где больше скорость течения жидкости (рис.2.11).
Рис. 2.11
Величина и направление вектора скорости V в жидкости могут меняться со временем, то и картина линий тока может непрерывно меняться. Если же вектора скорости в каждой точке пространства не меняются, то течение жидкости называют стационарным. Часть жидкости, ограниченная линиями тока, называется трубкой тока. Частицы жидкости, двигаясь внутри трубки тока, не пересекают ее стенок. Рассмотрим одну трубку тока и обозначим через S1 и S2 площади поперечного сечения в ней (рис.2.12). Тогда за единицу времени через S1 и S2 протекают одинаковые объемы жидкости: S1V1=S2V2 (2.47) это применимо к любому сечению трубки тока. Следовательно, для идеальной жидкости величина SV=const в любом сечении трубки тока. Это соотношение называется неразрывностью струи. Из него следует:
т.е. скорость V стационарного течения жидкости обратно пропорциональна площади сечения S трубки тока, а это может быть обусловлено градиентом давления в жидкости вдоль трубки тока. Теорема о неразрывности струи (2.47) применима и к реальным жидкостям (газам) при их течении в трубах разного сечения, если силы трения невелики. Уравнение Бернулли. Выделим в идеальной жидкости трубку тока переменного сечения (рис.2.12). В силу неразрывности струи через S1 и S2 за одно время протекают одинаковые объемы жидкости ΔV.
Рис. 2.12
Энергия каждой частицы жидкости складывается из ее кинетической энергии и потенциальной энергии. Тогда при переходе от одного сечения трубки токи к другому приращение энергии жидкости будет:
В идеальной жидкости приращение ΔW должно равняться работе сил давления на изменение объема ΔV, т.е. А=(Р1-Р2)· ΔV. Приравнивая ΔW=A и сокращая на ΔVи учитывая, что
т.к. сечение трубки тока взяты произвольно, то для идеальной жидкости вдоль любой линии тока выполняется:
где Р -статическое давление в определенном сечении S трубки тока;
ρgh -гидростатическое давление. Уравнение (2.48) называется уравнением Бернулли. Вязкая жидкость. В реальной жидкости при перемещении ее слоев относительно друг друга возникают силы внутреннего трения (вязкость). Пусть два слоя жидкости отстоят друг от друга на расстояние Δх и движутся со скоростями V1 и V2 (рис.2.13).
Рис.2.13
Тогда сила внутреннего трения между слоями (закон Ньютона):
где η -коэффициент динамической вязкости жидкости:
Слоистое течение жидкости называется ламинарным. При возрастании скорости слоистый характер течения нарушается, происходит перемешивание жидкости. Такое течение называют турбулентным. При ламинарном течении поток жидкости Q в трубе радиуса R пропорционален перепаду давления на единице длины трубы ΔР/ℓ:
В реальных жидкостях и газах движущиеся тела испытывают действия силы сопротивления. Например, сила сопротивления, действующая на шарик, равномерно движущийся в вязкой среде, пропорциональна его скорости V:
где r -радиус шарика. При увеличении скорости движения обтекание тела нарушается, позади тела образуются завихрения, на что дополнительно тратится энергия. Это приводит к возрастанию лобового сопротивления.
|
|||||||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 633; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |


 ,
,

 (ρ -плотность жидкости), получим:
(ρ -плотность жидкости), получим: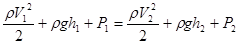
 . (2.48)
. (2.48) -динамическое давление для этого сечения; V-скорость протекания жидкости через это сечение;
-динамическое давление для этого сечения; V-скорость протекания жидкости через это сечение;
 , (2.49)
, (2.49) , (2.50)
, (2.50) - средняя арифметическая скорость молекул;
- средняя арифметическая скорость молекул; - средняя длина свободного пробега молекул;
- средняя длина свободного пробега молекул; -градиент скорости слоев; ΔS – площадь соприкасающихся слоев.
-градиент скорости слоев; ΔS – площадь соприкасающихся слоев. - формула Пуазейля. (2.51)
- формула Пуазейля. (2.51) - формула Стокса, (2.52)
- формула Стокса, (2.52)


