Электроемкость уединенного проводника конденсатора
Похожие статьи вашей тематики
Опыт показывает, что при сообщении заряда Q проводнику потенциал его изменяется пропорционально на величину φ. Коэффициент пропорциональности
 (3.24) (3.24)
называется электроемкостью (емкостью) проводника.
Единицей емкости является Фарад:  . .
Потенциал шара радиуса R согласно (3.16):
 . .
Сравнивая с (3.24), получим формулу емкости проводящего шара:
C = 4πε0 εR. (3.25)
Найдем радиус шара, емкость которого равна 1Ф:
 . .
Эта величина в 1400 раз больше радиуса Земли. Следовательно, Фарад очень большая единица емкости. Поэтому на практике емкость проводников (конденсаторов) измеряется в мкФ или пФ.
Для увеличения электроемкости проводников в технике используют устройства, называемые конденсаторами. Конденсатор состоит из двух проводников, обычно разделенных диэлектриком. Например, две параллельные плоские пластины, между которыми находится диэлектрик, образуют плоский конденсатор.
Электроемкость конденсатора определяется формулой, аналогичной (3.24):
 , (3.26) , (3.26)
где φ1-φ2-разность потенциалов между пластинами конденсатора;
σ-поверхностная плотность зарядов на пластинах;
S-площадь пластины.
При наличии диэлектрика между пластинами с диэлектрической проницаемостью ε>1 имеем φ1- φ2=Еd или с учетом формулы (3.12):
 . .
Подставив это значение разности потенциалов в (3.26), получим формулу для емкости плоского конденсатора:
 , (3.27) , (3.27)
где d – расстояние между пластинами.
Емкость сферического конденсатора:
С=4π ε ε0 r1 r2/(r2-r1), (3.28)
где r1 и r2-радиусы концентрических сфер.
Емкость цилиндрического конденсатора:
С=2π ε ε0 ℓ·ℓn·r1/r2, (3.29)
где ℓ- длина полых коаксиальных цилиндров радиусами r1 и r2.
Для увеличения емкости и варьирования ее возможных значений конденсаторы объединяют в батареи. При параллельном соединении емкость батареи:
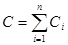 (3.30) (3.30)
При последовательном:
 . (3.31) . (3.31)
Энергия системы зарядов.
При формировании системы зарядов затрачивается энергия на преодоление их взаимодействия:
 , (3.32) , (3.32)
где φi -потенциал в точке, где находится заряд Qi, созданный всеми зарядами системы кроме Qi.
Энергия заряженного проводника
В соответствии с законом сохранения энергию W заряженного проводника можно определить как работу, которую затрачивают силы электрического поля проводника на его зарядку: заряд Q переносится малыми порциями dQ на проводник из бесконечности. Тогда элементарная работа, совершаемая при этом, согласно (3.17) равна:
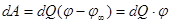 . .
Учитывая (3.24), получаем
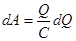 . .
Полная работа и соответственно энергия уединённого заряженного проводника:
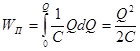 . (3.33) . (3.33)
или с учетом (3.24)
 . (3.34) . (3.34)
По формуле (3.33) и (3.34) можно определять энергию плоского конденсатора.
|