Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория Бора для водородоподобных атомов.Содержание книги
Поиск на нашем сайте
Нильс Бор, знаменитый датский физик в 1913 г для объяснения наблюдаемых особенностей в спектрах излучения атомов выдвинул три постулата: 1. В атомах существуют особые стационарные орбиты электронов, двигаясь по которым они не излучают и не поглощают энергию. Находясь в таких стационарных состояниях, атом имеет энергии, образующие дискретный ряд значений: Е1, Е2, Е3 … Еn, которые называют уровнями энергии атома. Стационарными могут быть только такие орбиты, на которых электрон имеет момент количества движения mVrn, кратный целому числу mVrn=n где m – масса электрона; V - его скорость на n-й орбите; rn – радиус n-й орбиты;
n – главное квантовое число (n = 1, 2, 3, ………, 2. Второй постулат (правило частот): атом излучает или поглощает квант энергии при переходе электрона из одного стационарного состояния в другое. Если электрон находится на первой орбите, то его энергия наименьшая из возможных; это нормальное состояние атома. Переход электрона на орбиту с n>1 может произойти только тогда, когда атом получит энергию извне (при поглощении фотона или при столкновении с другими атомами и частицами). Это ведет к возбуждению атома. Такое состояние атома малоустойчиво, и через некоторое малое время электрон возвращается в нормальное состояние. При этом испускается монохроматическое излучение с определенной длиной волны l, которой в спектре соответствует определенная линия. Частота n этого излучения может быть определена из соотношения: ε =hn =Еn – Ek, (5.27) где ε - квант энергии излучения (далее см. формулы 5.37 и 5.39); n- частота, излучаемая атомом при переходе электрона с n – ой орбиты на k - ю; Еn – энергия атома для n – ой орбиты до излучения; Еk – энергия атома после излучения для k – й орбиты. Для атома водорода можно найти радиус n – ой орбиты и полную энергию Еn стационарного состояния атома. Атом водорода состоит из одного протона (ядро) и одного электрона, он вращается по орбитам, которые будем считать окружности с радиусами rn. Сила притяжения электрона с элементарным зарядом е к ядру с таким же по величине зарядом е определяется законом Кулона (см. раздел 3.1). Она является центростремительной силой и удерживает электрон на орбите, т.е.
где ε0- электрическая постоянная Решая совместно уравнения (5.28) и (5.26), найдем радиус n-ой орбиты электрона
Для первой боровской орбиты электрона (n = 1) радиус будет иметь значение
(а 0=52,9·10-12 м). Тогда для любой n-ой орбиты rn= a 0n2 (5.31)
Полную энергию Е атома водорода найдем как сумму кинетической энергии движения электрона Е и потенциальной энергии U его взаимодействия с ядром (протоном в атоме водорода): Еn=E+U (5.32) Кинетическая энергия
Потенциальную энергию U рассчитаем как величину, численно равную работе А, необходимой для удаления электрона из атома с орбиты rn в бесконечность (
Подставляя в полученный результат величину rn из формулы (5.29), имеем
Сравнивая формулы (5.33) и (5)34, заметим, что U= -2E. Зная Е и U, можно, найти полную энергию стационарного состояния атома, для на n-ой стационарной орбиты
для k-ой стационарной орбиты
Подставляя Еn и Еk в формулу (5.27), получим уравнение для определения энергии ε, излучаемой (или поглощаемой) атомом при переходе электрона с одной орбиты на другую:
Удаление электрона из атома водорода (этот процесс называется ионизацией атома) требует затраты энергии, которая в соответствии с формулой (5.37) имеем величину
Еj называют энергией ионизации атома. Для атома водорода подсчитанная по формуле (5.38) величина
а формулу (5.35) для расчета энергии электрона в атоме водорода на любой n-ой орбите (или уровня энергии атома при данном квантовом числе n) можно переписать в виде
В нормальном состоянии (т.е. в невозбужденном атоме) электрон находится на стационарной орбите с n=1. Тогда энергия электрона, соответствующая основному состоянию атома водорода
Придавая другие значения числу n (2, 3, 4, …
Рис.5.8
Возвращение атома в нормальное состояние может происходить ступенчато, как показано на схеме (рис.5.8.). Например, возможен переход с любого уровня n≥2 на нормальный уровень 1. В спектре излучения водорода это соответствует серии линий Лаймана. Величина испущенных квантов энергии этой серии может быть вычислена по формуле (5.39.):
В спектре водорода серия линий Лаймана расположена в ультрафиолетовой области. Возможен также переход с любого вышележащего уровня на уровень k=2.
что ведет к излучению другой серии линий в спектре водорода, серии Бальмера (рис.5.8). Она лежит в видимой области спектра. Переход атомов с вышележащих уровней на уровни 3, 4, т.д. приводит к излучению новых серий в спектре водорода, также невидимых, лежащих уже в инфракрасной области. Так при k = 3 и n = 4, 5, 6, …,
Связь между квантом энергии ε и длиной волны λ можно получить по формуле Планка: ε = hc/l
Величина R=Ej/h называется постоянной Ридберга (R=1,1·107 м-1 или R=3,29·1015 с-1) Таким образом, теория Бора объяснила структуру спектра излучения атома водорода. Однако для более сложных атомов она уже не дает хороших результатов, отвечающих опытным данным. Для расчета λ можно воспользоваться формулой Бальмера:
где Z – номер элемента в таблице Менделеева. При больших квантовых числах n энергетические уровни (рис.5.8) сближаются и квантование энергии дает результаты, близкие к результатам классической физики – принцип соответствия Бора. Реально для электрона в атоме водорода уравнение Шредингера будет иметь вид (5.23), т.к. потенциальная энергия, определяющая взаимодействие электрона с ядром, не равна нулю (U¹0). Собственные функции, удовлетворяющие уравнению (5.23), будут содержать кроме главного числа n еще и другие параметры: ℓ - орбитальное квантовое число (ℓ=0, 1,2, …, n-1); m – магнитное квантовое число (m = 0, ±1, …, ±ℓ, ±(ℓ ± 1), т.е 2ℓ+1 значений). Таким образом, каждому Еn будет соответствовать набор волновых функций с различными ℓ и m. Это означает, что атом водорода может иметь одно и тоже значение энергии Еn, находясь в различных состояниях. Состояние с одинаковыми Еn называются вырожденными, а число различных состояний – кратностью вырождения. Электрон, движущийся в атоме, можно рассматривать как элементарный ток с собственным магнитным моментом (рис.3.24). В квантовой теории стационарными будут состояния, характеризуемые магнитным квантом числом m: Δрm = Эффект Зеемана. Линии спектров некоторых веществ обнаруживают тонкую структуру, т.е. состоят из нескольких близко расположенных линий. Так при наблюдении свечения паров Na в магнитном поле происходит расщепление линий спектра. Это навело на мысль, что электрон обладает, кроме орбитального, еще и собственным магнитным моментом и моментом количества движения L – спином. Спин является внутренним свойством электрона. Величина спина определяется спиновым квантовым числом S = ±1/2 (спином обладают протоны и др. частицы). Наличие спина у электрона подтверждено опытами Штерна и Герлаха, наблюдавшим расщепление пучка атомов водорода в магнитном поле.
Многоэлектронные атомы
При переходе к многоэлектронным системам следует сказать, что все электроны имеют одинаковые характеристики такие, как масса, заряд, квантовые числа. Такие частицы называют тождественными. В квантовой механике существует фундаментальный принцип – принцип неразличимости тождественных частиц. Все элементарные частицы и построенные из них атомы и молекулы делятся на два класса. Частицы с полуцелым спином (электроны, протоны, нейтроны) называются фермионами, частицы с нулевым или целочисленным спином (фотоны) называются бозонами. Принцип Паули: в системе тождественных фермионов любые два из них не могут одновременно находиться в одном и том же состоянии (т.е. не может быть двух электронов в одинаковом стационарном состоянии, определяемом набором квантовых чисел: n, ℓ, m и ms). Состояние электрона с ℓ = 0 называется S – состоянием; с ℓ = 1 р – состоянием; с ℓ = 2 d – состоянием; с ℓ = 3 f – состоянием; с ℓ = 4 g – состоянием и т.д. Так как ℓ при заданном n может принимать n-1 состояний, то максимальное число электронов будет 2n2. Они в атоме образуют оболочки K, L, M, N и т.д. Принцип Паули позволяет объяснить распределение элементов в таблице Менделеева. Молекулы
Молекула – структурная частица вещества, состоящая из атомов или ионов, находящихся в химической связи. Встречаются ионная и ковалентная связи. Ионная связь (NaCl, KOH и др.) обусловлена переходом электрона от одного атома к другому – образуется два иона (Na+ Cl-). Ковалентная связь (Н2, СО и др.) осуществляется за счет обобществления внешних (валентных) электронов соседними атомами –энергетически выгодный процесс. Молекула является квантовой системой и описывается уравнением Шредингера. Энергия изолированной молекулы складывается из Ее – энергии движения электронов, Ея – энергии колебательного движения ядер атомов, Евр – энергии вращения уровней ядер и др. Каждой энергии соответствует набор дискретных уровней энергии. Частота излучения, испускаемого при изменении состояния молекулы ν = Так как энергии молекулы представляют набор дискретных уровней, то спектр молекулы состоит из отдельных линий, группирующихся так тесно, что молекулярные спектры в отличии от атомных являются полосатыми.
Электроны в кристаллах
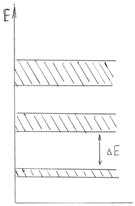
Кристалл характеризуется упорядоченным расположением атомов в объеме тела и более сильными межатомными связями, позволяющими удерживать атомы в узлах кристаллической решетки. Находясь в узлах, атомы участвуют в тепловых колебаниях около положения равновесия и только при достижении точки плавления эти связи разрываются и решетка распадается. Кристалл характеризуется анизотропностью, т.е. изменчивостью физических свойств в разных кристаллографических направлениях. В ионных кристаллах (типа NaCl) силы взаимодействия между ионами имеют электрическую природу. В атомных кристаллах электрически нейтральные атомы в узлах удерживаются ковалентными связями. В металлических кристаллах валентные электроны слабо связаны с атомами и ведут себя как свободные электроны, ответственные, в частности, за проводимость металлов. Электроны в изолированном атоме находятся в потенциальной яме (см. п.5.3.), образуя ряд дискретных энергетических уровней, что следует из теории Шредингера. В кристалле периодическое электрическое поле изменяет энергетические состояния электронов- учитывается их взаимодействие с соседними атомами решетки. В результате энергетические уровни расщепляются. Совокупность близко расположенных уровней образует энергетическую зону. Пользуясь соотношением неопределенностей (см. п. 5.2. формула 5.20) при времени жизни электрона в поле одного атома τ = 10-15 с, можно определить ширину зоны ΔЕ дозволенных уровней энергии в кристалле. Между зонами дозволенных уровней существуют зоны запрещенных значений энергии (на рис. 5.10 незаштрихованы).
Рис.5.9
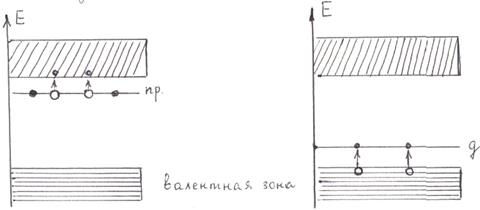
Разрешенные (заштрихованные на рис.5.9) зоны могут быть по разному заполнены электронами, которые внутри этих зон могут переходить с одного энергетического уровня на другой с малыми затратами энергии. Переход в другую разрешенную зону через запрещенную требует больших затрат энергии порядка нескольких эВ. Валентные электроны могут частично или полностью заполнять уровни разрешенной зоны. Если в ней остаются незаполненные уровни, то электроны, поглощая энергию, могут переходить на более высокие энергетические уровни и участвовать в проводимости тока металлом (эта зона соответственно называется зоной проводимости). Такими свойствами обладают металлы первой группы таблицы Менделеева. При температуре 0 К электроны в соответствии с принципом Паули не могут все находиться на самом низшем энергетическом уровне, а распределяются по уровням в зоне проводимости. Самая верхняя зона, целиком заполненная электронами при 0 К называется валентной, при этом будут заполнены все уровни вплоть до максимального с энергией Ферми. Для металлов она велика и лишь незначительная часть электронов при Т>0 К может превышать энергию Ферми. Наивысший уровень, занятый электронами, называется уровнем Ферми. У щелочно - земельных металлов наблюдается перекрытие разрешенных зон с образованием гибридной зоны. Эти металлы тоже являются проводниками. У твердых диэлектриков энергетические зоны не перекрываются, при этом валентная зона отделена от зоны проводимости запрещенной зоной в несколько эВ. У полупроводников этот интервал уже (от сотых долей до 3 эВ). Поэтому всегда есть вероятность при Т>0 К, что часть электронов перейдет в зону проводимости и под действием электрического поля будут проводить ток (электронная проводимость n-типа). В валентной зоне при уходе электронов образуются дырки, на их места из нижележащих уровней могут во внешнем электрическом поле переходить электроны. Такой процесс заполнения дырок электронами равносилен перемещению самих дырок в противоположном электронам направлении – дырочная проводимость р - типа. Таким образом, собственная проводимость полупроводников связана как с перемещением электронов так и дырок, т.е. будет электронно-дырочной. С повышением температуры растет число электронов и дырок, обеспечивающих проводимость собственного полупроводника и в отличии от металлов сопротивление току у него при нагревании падает. При введении примесей в полупроводник проводимость его существенно меняется. Примесная проводимость полупроводников связана с внедрением в их кристаллическую решетку атомов другого элемента с большей (электронная n – проводимость) или меньшей (дырочная р – проводимость) валентностью. Например, четырехвалентный кремний можно легировать пятивалентным фосфором (донорная примесь) или трехвалентным бором (акцепторная примесь). При замещении атома кремния атомом пятивалентного фосфора один электрон оказывается свободным от ковалентной связи атомов кремния. Его энергия выше, чем у связанных электронов и энергетический уровень будет находиться в запрещенной зоне (примесный уровень, рис.5.11,а). При Т>0 К этот уровень может переместиться в зону проводимости, обеспечивая полупроводнику электронную примесную проводимость n – типа. При легировании трехвалентным бором одной электронной связи у атомов кремния будет недоставать, т.е. образуется дырка. В запрещенной зоне возникает примесный энергетический уровень – донорный (рис. 5.11, б), он может заполняться электронами из валентной зоны, что приведет к перемещению дырки (дырочная проводимость р - типа).
Рис. 5.10.
В отличии от собственной примесная проводимость полупроводников будет обусловлена или электронами (n – типа), или дырками (р – типа). Наличие примесей приводит к смещению уровня Ферми, находящемуся между валентной зоной и зоной проводимости. При контакте двух полупроводников с различной проводимостью образуется р-n-переход, обладающий односторонней проводимостью. Это связано с тем, что в зоне контакта вследствие диффузии электронов и дырок образуется двойной электрический слой (рис.5.12,а). Удельное сопротивление этого запирающего слоя значительно больше, чем в остальном объеме полупроводника. Двойной слой создает контактное электрическое поле с некоторой разностью потенциалов. Это поле прекращает дальнейшее встречное движение электронов и дырок, происходит выравнивание уровней Ферми в обоих полупроводниках.
а)б)
Рис.5.11
При включении электрического поля в зависимости от полярности приложенной ЭДС источника толщина и сопротивление запирающего слоя могут либо уменьшиться и ток через р-n - переход проходит, возрастая с ростом напряжения U (рис.5.12, б), либо наоборот, сопротивление увеличится и ток через р-n переход практически не проходит (обратный ток). Это позволяет использовать полупроводниковые диоды для выпрямления тока. Полупроводниковые устройства с двумя р-n переходами называются транзисторами и служат для усиления напряжения, тока или мощности. Существуют также фотоэлементы с р-n переходом.

а) б) Рис. 5.12.
Сверхпроводимость заключается в том, что у некоторых веществ происходит резкое падение удельного сопротивления при определенной температуре. В настоящее время известно несколько сотен сверхпроводящих металлов и сплавов. Сильное магнитное поле разрушает сверхпроводящее состояние. Возникновение сверхпроводимости объясняется образованием в веществе пар электронов с противоположными спинами (куперовских пар). Спин у пары в итоге равен нулю и она представляет собой бозон, на который принцип запрета Паули не распространяется. Поэтому при очень низких температурах бозоны могут накапливаться на нижних энергетических уровнях. Такие бозоны под действием внешнего электрического поля легко приходят в движение, их взаимодействие с узлами решетки ничтожно, что и означает отсутствие сопротивления току. Джозефсон обнаружил протекание тока в состоянии сверхпроводимости через тонкие пленки диэлектрика благодаря туннельному эффекту для электронов. При этом падения напряжения на пленках (границах сверхпроводников) нет. При достижении некоторого критического значения тока падение напряжения возникает и пленка излучает электромагнитные волны с определенной частотой. Это излучение связано с изменением состояния куперовских пар на границе сверхпроводников. Эффект Джозефсона применяют для создания быстродействующих элементов логических схем ЭВМ. Явление сверхпроводимости используется для создания сильных магнитных полей при отсутствии теплового нагрева (в ускорителях, генераторах, и т.п.).
|
||||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 1763; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 :
: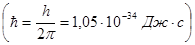 ;
; ).
).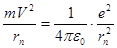 , (5.28)
, (5.28) .
. (5.29)
(5.29)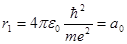 (5.30)
(5.30)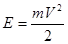 . С учетом формул (5.28.) и (5.29.) имеем
. С учетом формул (5.28.) и (5.29.) имеем (5.33)
(5.33)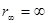 ):
):
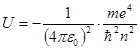 (5.34)
(5.34) , (5.35)
, (5.35)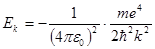 (5.36)
(5.36)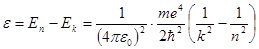 (5.37)
(5.37)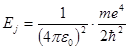 (5.38)
(5.38) Дж (или 13,6 эВ). Формулу (5.37) можно также выразить через Еj:
Дж (или 13,6 эВ). Формулу (5.37) можно также выразить через Еj: , (5.39)
, (5.39)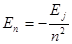 (5.40)
(5.40) Дж (или –13,6 эВ).
Дж (или –13,6 эВ).
 , n = 2, 3, 4, …,
, n = 2, 3, 4, …,  , n = 3, 4, 5, …,
, n = 3, 4, 5, …,  и т.д.
и т.д. , (5.41)
, (5.41)