
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерференция от двух когерентных источниковСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Пусть имеются два когерентных источника S1 и S2 (рис.4.7).
Рис.4.7
Волны от них приходят в точку В, отстоящую от источников на расстояниях у1 и у2, и интерферируют. Рассмотрим условия наблюдения максимума или минимума в этой точке. Будем для простоты считать, что амплитуда колебаний А0 одинакова,
одинаковы и плоскости колебаний векторов А. Амплитуда в точке В в результате интерференции по принципу суперпозиции волн будет равна сумме:
Из тригонометрии известно, что
Величина Очевидно, что амплитуда колебаний вектора А будет максимальной при разности хода лучей Δ, равной целому числу m длин волн или четному числу 2m полуволн, т.е. при:
так как Также можно показать, что при разности хода равной нечетному числу (2m+1) полуволн, т.е. при
колебания ослабляют друг друга. Наблюдается минимум интенсивности. На экране Э в области, где волны накладываются, будет наблюдаться чередование максимумов и минимумов. Это и есть интерференционная картина (рис.4.7). Определим координаты х максимумов и минимумов:
откуда Полагая, что d<<L, можно считать Из (4.23)
для минимума Минимальное расстояние между минимумами (или максимумами) определит ширину интерференционной полосы (рис.4.7)
Пусть S1 и S2 на рис 4.7 являются источниками света. Световым вектором принято считать вектор электрической напряженности При наложении световых волн от двух источников:
интенсивность света в точке В (рис.4.7) будет определяться (с учетом 4.20):
На экране Э будут наблюдаться чередующиеся светлые и темные интерференционные полосы разной интенсивности в соответствии с условиями максимума (4.21) или минимума (4.22). Если свет распространяется не в вакууме, а в среде с оптической плотностью n>1, то оптическая разность хода лучей Δ=y2n-y1n=(y2-y1)n. При интерференции происходит перераспределение световой энергии, т.е. закон сохранения энергии не нарушается. В конце прошлого века сформировалось представление о свете, как имеющем двойственную природу - волновую и квантовую. Сочетались, казалось бы исключающие друг друга волновые (дифракция, интерференция, поляризация) и квантовые (фотоэффект, эффект Комптона и др.) свойства света. Естественный свет (например, солнечный) в видимом для человека диапазоне представляет собой электромагнитные волны длиной от 0,4 до 0.76 мкм и частотой 1015 Гц. Волны с длиной меньше 0,4 мкм называется ультрафиолетовыми, а с длиной больше 0,76 мкм - инфракрасными (тепловое излучение). Как было уже рассмотрено (см.п.3.5), в электромагнитной волне электрический вектор Если S1 и S2-источники естественного света, то на экране Э (рис.4.7) интерференционные светлые полосы будут иметь радужную окраску (из семи цветов), т.к. оптическая разность хода лучей Δ зависит от λ (см.4.21). Стоячие волны Если две одинаковые бегущие волны распространяются вдоль оси “у” навстречу друг другу, то при наложении этих волн возникают колебания среды, называемые стоячей волной. Для получения уравнения стоячей волны сложим уравнения (4.17) в одной точке:
Произведя тригонометрические преобразования, найдем:
это и есть уравнение стоячей волны.
Величина
есть амплитуда волны. Она зависит от координаты “у” колеблющейся в волне точки и не зависит от времени t, т.е. не наблюдается волнового движения и переноса энергии (отсюда и название -стоячая волна). В точках, в которых выполняется условие
амплитуда стоячей волны максимальна и равна 2А (пучности волны). В точках, где
Рис. 4.8
наименьшее расстояние между соседними пучностями или узлами равно λ/2. Стоячие волны образуются при колебаниях в телах ограниченных размеров вследствие отражения их от границ тел, (например, при колебаниях струны).
|
|||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 1322; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |




 или в нашем случае:
или в нашем случае: (4.20)
(4.20) есть амплитуда вектора А результирующего колебания, полученного при наложении двух волн в точке В (рис.4.7). Она является периодической функцией разности хода лучей Δ = y2 - y1 и не зависит от времени t.
есть амплитуда вектора А результирующего колебания, полученного при наложении двух волн в точке В (рис.4.7). Она является периодической функцией разности хода лучей Δ = y2 - y1 и не зависит от времени t. , (4.21)
, (4.21) принимает максимальное значение, а разность фаз колебаний Δφ будет кратным 2π (см. 4.19). Величину m называют порядком интерференции (m=0, 1, 2, 3…).
принимает максимальное значение, а разность фаз колебаний Δφ будет кратным 2π (см. 4.19). Величину m называют порядком интерференции (m=0, 1, 2, 3…). (4.22)
(4.22)
 или
или  (4.23)
(4.23) ,
,  дает разность хода волн.
дает разность хода волн.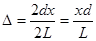 . С учетом (4.21) для координаты максимума получим:
. С учетом (4.21) для координаты максимума получим:


 . Как показывает опыт, зрительные ощущения, фотоэлектрическое, фотохимическое действия света, вызывают колебания именно электрического вектора Е. Интенсивность I света пропорциональна квадрату амплитуды светового вектора Е2.
. Как показывает опыт, зрительные ощущения, фотоэлектрическое, фотохимическое действия света, вызывают колебания именно электрического вектора Е. Интенсивность I света пропорциональна квадрату амплитуды светового вектора Е2.

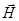 колеблются во взаимно перпендикулярных плоскостях поперек направления распространения волны (световые волны - поперечные волны).
колеблются во взаимно перпендикулярных плоскостях поперек направления распространения волны (световые волны - поперечные волны).
 (4.23)
(4.23)
 (m=0, 1, 2, 3,…)
(m=0, 1, 2, 3,…) , амплитуда стоячей волны обращается в нуль. Эти точки называются узлами стоячей волны. Из рис. 4.8 видно, что
, амплитуда стоячей волны обращается в нуль. Эти точки называются узлами стоячей волны. Из рис. 4.8 видно, что



