
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Российский государственный открытыйСодержание книги
Поиск на нашем сайте РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
Аммер С.А., Карелин Б.В.
ФИЗИКА
УЧЕБНОЕ ПОСОБИЕ
Курс лекций для студентов технических Специальностей
Воронеж 2004
УДК 53 ББК 32 А 73
Физика. Учебное пособие. С.А.Аммер, Б.В.Карелин. Российский гос.откр.техн.университет путей сообщ. В. 2004 Курс лекций по физике для студентов технических специальностей написан в соответствии с программой и преследует цель помочь студентам, обучающимся без отрыва от производства, овладеть основами физической науки при внедрении современных методов информационных технологий.
Рецензент:
ВВЕДЕНИЕ
Физика – одна из фундаментальных наук. Неоценима ее роль в современной интеграции естественных наук, построении научной картины мира и формировании мировоззрения и экологического мышления. Физика – это наука о наиболее общих свойствах и формах движения материи, о наиболее общих законах природы. Физика – наука экспериментальная, т.е. в основе методов познания природы лежит эксперимент. Для объяснения опытных данных выдвигаются гипотезы – научные предположения. Правильность их опять проверяется в опытах. Только после подтверждения правильности гипотеза становится научной теорией. Физика тесно связана с другими науками (философией, химией, биологией, астрономией, и др.), имеет с ними лишь условные границы. Тесно связана физика и с математикой, которая дает ей методы и математический аппарат исследований. Большинство физических законов имеют четкое математическое выражение. Стимулом к развитию физических исследований служили потребности человека, его стремление облегчить труд, удовлетворить свою любознательность. Открытия в области физики способствовали развитию новых отраслей техники. В свою очередь, техника, развиваясь, ставила новые проблемы перед физикой. При этом сама физическая наука обогащалась новыми техническими средствами. Например, открытие и изучение элементарных частиц было бы немыслимо без мощных ускорителей и другой сложной аппаратуры. Компьютеризация облегчила и ускорила научный поиск, расширила его возможности. Велик вклад в современную физику таких российских ученых как Иоффе, Мандельштам, Вавилов, Курчатов, лауреатов нобелевской премии академиков Ландау, Тамма, Черенкова, Прохорова, Франка, Басова, Капицы, Алферова и др. Законы физики устанавливаются связь между физическими величинами, единицами их измерения; с 1963 г. в нашей стране введена Международная система единиц СИ.
ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ
Механика рассматривает ограниченный круг вопросов, связанных с механическим движением материальных тел и происходящими при этом их взаимодействиями. Под механическим движением понимается изменение с течением времени взаимного положения тел или их частей в пространстве. Время характеризует последовательность, длительность событий. Пространство - расположение материальных объектов, их протяженность. Основы механики были заложены итальянским ученым Галилеем (1564-1642) и английским физиком Ньютоном (1643-1727). Классическая механика, рассматривает движение макроскопических тел со скоростями, значительно меньшими скорости света. Она базируется на следующих постулатах: 1. Действие одних тел на другие распространяется мгновенно. 2. Пространство и время независимы друг от друга, абсолютны и изотропны. 3. Масса рассматривается как мера количества вещества. В начале ХХ века эти постулаты подверглись кардинальному пересмотру, что привело к созданию одной из величайших научных теорий-теории относительности. По Эйнштейну пространство и время неотделимы от материи и ее движения и имеют относительный, а не абсолютный характер. Свойства пространства и времени оказались зависимы от материальных тел и их движения. Быстрые движения макроскопических тел со скоростями, близкими к скорости света, рассматривает релятивистская механика или специальная теория относительности. Свойства и движения микрочастиц описывает квантовая механика. Теория относительности и квантовая механика не отвергают классическую механику, они развивают ее на принципиально новой основе. Материальная точка. Любое тело, размерами и формой которого можно пренебречь в данных условиях, называют материальной точкой. Массу теласчитают сосредоточенной в данной точке. 2. Абсолютно твердое тело. Тело можно представить как систему материальных точек, жестко связанных между собой, т.е. можно пренебречь изменением расстояний между ними. Такое тело называют абсолютно твердым. 3. Удобно также рассматривать движение тел в среде, не вникая в ее атомарно-молекулярное строение. Такую среду называют сплошной.
Рис.2.1
При этом тело пройдет путь, равный длине дуги ℓ12 между точками 1 и 2 за время t. За это же время t радиус- вектор R, проведенный из центра окружности 0 к точке, повернется на угол Δφ. Вектор скорости в точке 2 отличается от вектора скорости в точке 1 по направлению на величину ΔV:
Для характеристики изменения вектора скорости на величину ΔV введем ускорение
Вектор Если скорость
Направлен вектор Полное ускорение точки, движущейся по криволинейной траектории, определяется как векторная сумма (рис.2.1.).
Модуль вектора
Центр масс Действие одного тела на другое характеризуется силой. Сила – это физическая величина, являющаяся мерой механического действия одного тела на другое. Масса – является мерой инертности материальных тел. Второй закон Ньютона: ускорение а, полученное телом, прямо пропорционально приложенной силе F и обратно пропорционально его массе m:
Направление вектора В ньютоновской механике масса не зависит от скорости движения (это верно лишь при скоростях V<<C, где С – скорость света в вакууме). Уравнение (2.13) можно переписать, учитывая что
где m Второй закон Ньютона с учетом (2.14) можно сформулировать иначе: скорость изменения импульса Р материальной точки равна действующей на нее силе или Если на тело одновременно действует несколько сил: В системе – СИ за единицу массы принят 1 кг. За единицу силы – 1 Н (один Ньютон).
1Н=1кг ·1м/с2=1кг · м · с-2. Центр масс. Любое тело можно представить как систему материальных точек с массой mi. Для каждой из них можно записать Таким образом, вместо движения твердого тела можно рассмотреть движение одной материальной точки С с массой, равной массе всего тела, под действием силы, равной главному вектору сил. Такая точка называется центром масс (центром инерции). Координаты центра масс в проекциях на оси координат определяют следующим образом:
Третий закон Ньютона: тела действуют друг на друга с силами, направленными вдоль одной прямой, равными по абсолютным значениям и противоположными по направлению.
При этом силы Рис.2.3
Кратчайшее расстояние от оси вращения О до направления действия силы, т.е. длина перпендикуляра, опущенного из оси О на направление действия силы, называют плечом силы: ℓ1 – плечо силы F1, М1=F1ℓ1 ℓ2 – плечо силы F2, M2=F2ℓ2
Из рисунка 2.3 видно, что плечо ℓ1=r1sinα. Тогда момент силы М можно записать: М=rFsinα. (2.16) Первая часть равенства (2.16) есть модуль векторного произведения Направление Правило моментов: тело, способное вращаться вокруг неподвижной оси, будет находиться в равновесии, если алгебраическая сумма моментов приложенных сил относительно оси вращения равна нулю
Моментом импульса L материальной точки относительно неподвижной оси О называется векторное произведение радиуса вектора
где J -момент инерции тела. Момент импульса механической системы относительно неподвижной оси
Для замкнутой системы тел закон сохранения момента импульса: момент импульса замкнутой системы тел есть величина постоянная, если векторная сумма моментов всех внешних сил равна нулю.
Единица измерения момента импульса [L]=кг · м2/с.
Энергия. Работа. Мощность Энергия есть физическая величина, характеризующая способность тела или системы тел совершать работу. Энергия в механике может быть обусловлена причинами двоякого рода: во-первых, движением тела с некоторой скоростью (кинетическая энергия) и, во-вторых, нахождением тела в потенциальном поле сил (потенциальная энергия). Для количественной оценки изменения энергии тела вводят понятие работы как меры изменения энергии. В общем случае элементарная работа δА силы
где α - угол между Произведение F · cosα = Fr есть проекция
Рис.2.4
Работа силы
На рис.2.4. эта работа А12 численно равна площади криволинейной трапеции r112 r2. Если сила при перемещении не меняется (F=const), то
и на графике F-r будет численно равна площади прямоугольника. Работа положительна (А>0), если В системе СИ работа измеряется в Джоулях (Дж): 1 Дж = 1 Н · м
Мощность.
Мощность N силы F равна отношению элементарной работы δА ко времени dt, за которое она совершена, т.е.
где Таким образом, мощность силы можно определить как скалярное произведение векторов В системе СИ мощность измеряется в Вт.
Кинетическая энергия. Результатом действия силы
Поскольку В ньютоновской динамике масса m не зависит от скорости и тогда, интегрируя и полагая Wкo=0 при Vo=0, получим выражение для кинетической энергии материальной точки:
Величина Если на тело действует сила (или несколько сил, равнодействующая которых не равна нулю), то работа этой силы (или равнодействующей) равна изменению кинетической энергии тела. Это есть теорема о кинетической энергии: ΔWk=A. Если работа А>0, то кинетическая энергия тела возрастает, и наоборот. Кинетическая энергия (как энергия вообще) измеряется в Джоулях, как и работа.
Закон сохранения энергии
Рассмотрим пример превращения механической энергии при падении тела, принимаемого за материальную точку, с высоты h над поверхностью Земли. В начале падения скорость тела V0=0, кинетическая энергия Wк=0, потенциальная энергия его Wп=mgh (при малом перемещении изменением ускорения g силы тяжести можно пренебречь). В момент падения на Землю тело имеет скорость
Таким образом, кинетическая энергия тела при падении оказалась равной его потенциальной энергии до начала падения (сопротивление воздуха не учитываем). При этом потенциальная энергия на поверхности Земли (h=0) Wn=0, Wк=max. В начале падения Wк=0, Wn=max. Во всех промежуточных точках сумма Wк + Wn = const (2.24) Формула (2.24) выражает закон сохранения энергии в механике. Сумму кинетической и потенциальной энергии называют полной механической энергией. Поэтому закон сохранения энергии можно сформулировать так: полная механическая энергия замкнутой системы тел, взаимодействующих только консервативными силами, остается неизменной. Законы сохранения энергии и импульса тел – фундаментальные законы природы. Закон сохранения энергии выполняется не только в механике, он имеет и более общий смысл: в замкнутой системе тел полная энергия системы количественно остается неизменной. При этом тела могут обмениваться энергией. Например, при торможении поезда часть механической энергии переходит в тепловую. При сгорании топлива химическая энергия частично превращается в тепловую, частично в световую и т.д. В механизмах и машинах нельзя получить больше работы, чем затрачено энергии. Часть энергии теряется (на преодоление силы трения, обращается в тепло), поэтому полезная работа машины всегда меньше затраченной энергии: Аn<Wз, и к.п.д. Другим важнейшим свойством законов природы является свойство симметрии. Оно выражается в равномерности хода времени и означает, что относительная скорость всех процессов в природе постоянна. Равномерность хода времени установлена экспериментально с большой точностью на примере излучения света звездами и земными источниками. Речь идет о всеобъемлющем свойстве природы: все законы природы инвариантны относительно переноса в пространстве (см. также раздел 7).
ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
Электромагнитное взаимодействие относится к фундаментальным взаимодействиям в природе. Раздел классической физики, изучающий свойства и законы взаимодействия зарядов посредством электромагнитных полей, называется электродинамикой. В ее основе лежит теория Максвелла, доказавшего в 1860-х годах единство электрических и магнитных полей.
Электростатика
Электростатика рассматривает взаимодействие неподвижных электрических зарядов. Установлено, что любой электрический заряд Q кратен элементарному заряду е=1,6·10-19 Кл, то есть Q=en. Носителем элементарного положительного заряда принято считать протон, отрицательного - электрон. Электрические заряды могут перераспределяться в пределах одного тела или переходить с одного тела на другое, но в замкнутой системе алгебраическая сумма зарядов остается постоянной. Это положение называется законом сохранения заряда. Заряд называется точечным, если размеры тела, на котором он сосредоточен, пренебрежимо малы в сравнении с расстоянием до других зарядов.
Закон Кулона
Французский физик Ш. Кулон опытным путем установил, что два точечных заряда Q1 и Q2, находящиеся на расстоянии r, взаимодействуют в вакууме с силой
где ε0=8,85·10-12 Ф/м называется электрической постоянной. Формула (3.1) справедлива также и для заряженных шаров. В этом случае r – расстояние между центрами шаров. Одноименные заряды отталкиваются, разноименные- притягиваются друг к другу. Если взаимодействие зарядов происходит в среде с диэлектрической проницаемостью ε>1, то сила их взаимодействия уменьшается в ε раз (см.п.3.4), то есть закон Кулона в общем виде имеет вид
Электрическое поле
Вокруг зарядов образуется электрическое поле – это особая форма материи, связывающая заряды в единой системе и передающая с конечной скоростью (в вакууме – это скорость света) действие одних зарядов на другие. Квантом взаимодействия является фотон. Поле неподвижных зарядов называется электростатическим. Силовой характеристикой электрического поля служит векторная величина
Направления векторов
Как будет показано ниже, Н/Кл=В/м. Напряженность поля точечного заряда Q (и шара или сферы радиуса R при r>R):
Энергия системы зарядов. При формировании системы зарядов затрачивается энергия на преодоление их взаимодействия:
где φi -потенциал в точке, где находится заряд Qi, созданный всеми зарядами системы кроме Qi.
Закон Ома
Для однородного участка цепи
Сопротивление R зависит от длины проводника ℓ и площади S его поперечного сечения:
где ρ- удельное сопротивление, зависящее от материала проводника. Величина I/ρ называется удельной проводимостью. Для участка цепи с ЭДС:
Закон Ома в интегральной форме для полной цепи: сила тока в замкнутой цепи пропорциональна алгебраической сумме всех ЭДС, действующих в цепи, и обратно пропорциональна ее полному сопротивлению, равному сумме сопротивлений внешнего R и внутреннего Ri участков цепи:
Закон Джоуля-Ленца
При протекании постоянного тока по проводнику в нем выделяется количество тепла Q: Q= I2Rt=UIt (3.48) Когда ток постоянен, а проводник неподвижен, то вся работа сторонних сил расходуется на его нагревание. Если сила тока меняется, то количество тепла dQ, выделившегося на сопротивлении R за время dt при прохождении через него электрического тока: dQ Пусть сила тока I является некоторой функцией времени. В случае:
где k-коэффициент пропорциональности, характеризующий скорость изменения силы тока:
С учетом этого, формула (3.49) примет вид: dQ= (I0 + kt)2 Rdt Для определения тепла, выделившегося за конечный интервал времени Δt, проинтегрируем в пределах от t1 до t2: Q= Если начальный ток I0=0, то: Q= Магнитное поле
В 1820 году датский физик Эрстед обнаружил, что протекающий по проводнику ток действует на магнитную стрелку. Опыт показал также, что неподвижные заряды не создают вокруг себя магнитное поле. В отличии от электростатического магнитное поле имеет вихревой характер, т.е. линии этого поля всегда замкнуты (рис.3.10). Направление линий определяется правилом буравчика или правой руки.
Рис.3.10
Основной характеристикой магнитного поля является вектор магнитной индукции Кроме вектора магнитной индукции
где m - магнитная проницаемость среды (для вакуума m=1);
Сила Лоренца действует на заряд Q, движущийся в магнитном поле с индукцией В со скоростью V
где α - угол между векторами Сила Лоренца равна нулю, когда заряд движется вдоль магнитного поля (sinα =0), и максимальна, когда заряд движется перпендикулярно к нему (sinα =1). Направление Fл определяется по правилу левой руки (для положительного заряда). Ладонь располагается так, чтобы линии индукции в нее входили, четыре пальца указывали направление вектора скорости движения заряда. Тогда отставленный большой палец укажет направление действия силы. При движении отрицательного заряда сила направлена в противоположную сторону (рис.3.11).
а) б) Рис.3.11
Пусть положительный заряд Q движется перпендикулярно линиям вектора магнитной индукции Частица в данном случае будет двигаться по окружности в плоскости, перпендикулярной магнитному полю. Радиус R этой окружности найдем из условия, что сила Лоренца является здесь центростремительной силой.
Тогда Далее по формулам V = wR = 2pnR = В общем случае угол α в формуле (3.54) не обязательно равен 900. Тогда заряд будет двигаться в магнитном поле по винтовой линии с периодом Эффект Холла заключается в том, что при протекании тока в проводнике или полупроводнике в них возникает поперечная току разность потенциалов Δφ. Этотакже можно объяснить действием силы Лоренца на подвижные заряды (ток). Рассмотрим пластину с током I, перпендикулярным постоянному магнитному полю с индукцией В (рис.3.12)
Рис. 3.12
Под действием силы Лоренца Fл = QVB происходит разделение зарядов и между поверхностями пластин создается разность потенциалов Δφ. Возникшее электрическое поле действует на заряды с силой
тогда где K -постоянная Холла. Определив K, можно рассчитать концентрацию носителей. Сила Ампера действует на элемент тока dℓ в магнитном поле с индукцией В
где α-угол между вектором Направление силы Ампера F находится по правилу левой руки: вектора
Рис.3.13
Из формулы (3.56) следует, что если F = 1H, I = 1A, ℓ= 1м, то В будет 1 Тл (Тесла)
1Тл = т.е. 1 Тл это индукция такого магнитного поля, которое на проводник длиной 1 м с током в 1 А действует с силой в 1 Н. Магнитный момент контура с током:
где S-площадь контура;
Вектор рm перпендикулярен к площади контура и определяется правилом буравчика, вращаемого по току (рис.3.14)
Рис. 3.14 Явление самоиндукции
Это явление заключается в возникновении Э.Д.С. в контуре с током I в моменты изменения этого тока. Ток образует собственное магнитное поле за счет своей энергии. Магнитный поток, образованный током, пропорционален силе тока.
Ф = L · I (3.72)
Коэффициент пропорциональности L называется индуктивностью или коэффициентом самоиндукции контура. По определению а) от магнитной проницаемости среды; б) от размеров и формы контура (см. формулу 3.74). За единицу индуктивности в СИ принимается Генри (Гн). При изменении силы тока в контуре изменится и величина магнитного потока, пронизывающего контур. Но всякое изменение магнитного потока через контур, вызывает появление ЭДС индукции
Здесь знак «минус» указывает, что Э.Д.С. самоиндукции противодействует всякому изменению силы тока в контуре (правило Ленца). Следовательно, наличие индуктивности у контура приводит к своеобразной электрической инертности (что равносильно сопротивлению). Любое изменение тока в контуре тормозится и тем сильнее, чем больше его индуктивность L. Величина εS может достигать больших значений, что важно учитывать при резких изменениях силы тока в цепях с большой индуктивностью L (см. токи замыкания и размыкания). Индуктивность соленоида (когда ℓ>>d):
где n -плотность намотки ( ℓ -длина катушки (соленоида); S -площадь сечения катушки; d -ее диаметр; μ -магнитная проницаемость сердечника; V -объем катушки.
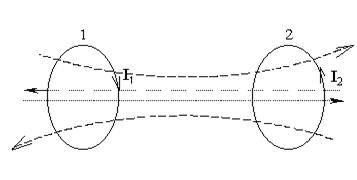
Явление взаимоиндукции
Рассмотрим два контура с токами I1 и I2 (рис.3.21):
Рис. 3.21
Первый контур создает магнитный поток Ф1=L1I1. Второй контур-Ф2=L2I2. При изменении токов и магнитных потоков в контурах будут индуцироваться ЭДС: в первом контуре - во втором контуре - Контуры 1 и 2 называются связанными, а явление возникновения εi в одном из них при изменении тока в другом называется взаимоиндукцией. Коэффициенты L12 и L21 – коэффициентами взаимоиндукции контуров или взаимными индуктивностями. На явлении взаимной индукции основан принцип действия трансформаторов. Коэффициент трансформации Энергия магнитного поля
Определим работу А, которую совершает ЭДС на увеличение тока в контуре от 0 до I. С учетом (3.69) и (3.72):
Эта работа, совершается против ЭДС самоиндукции, возникающей в контуре при увеличении тока. Иначе говоря, это работа тока затрачена на образование магнитного поля с энергией
Для соленоида
откуда объемная плотность энергии:
или с учетом (3.53):
Статические поля в веществе Магнитные свойства вещества
Вещества, способные намагничиваться под действием внешнего магнитного поля, называются магнетиками. Их можно разделить на три группы: а) парамагнетиками: при намагничивании усиливают внешнее магнитное поле, т.е. создают свое собственное магнитное поле б) диамагнетики: при намагничивании ослабляют внешнее магнитное поле, т.е. создают свое собственное магнитное поле в) существует, однако, вещества, для которых Н/ може
|
|||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 536; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.015 с.) |

 ;
; :
: (2.4)
(2.4) по направлению, называют центростремительным или нормальным. Таким образом, движение точки по окружности с постоянной по модулю скоростью является ускоренным.
по направлению, называют центростремительным или нормальным. Таким образом, движение точки по окружности с постоянной по модулю скоростью является ускоренным. , которое характеризует изменение скорости по величине:
, которое характеризует изменение скорости по величине: или
или 
 .
. .
. (2.13)
(2.13) всегда совпадает с направлением вектора силы
всегда совпадает с направлением вектора силы 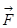 .
. ,
, , (2.14)
, (2.14) – называется импульсом (или количеством движения) тела. Тогда
– называется импульсом (или количеством движения) тела. Тогда  .
. .
.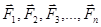 , то нужно найти их результирующую
, то нужно найти их результирующую 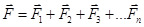 , а затем ускорение
, а затем ускорение 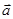 (принцип суперпозиции сил).
(принцип суперпозиции сил). . Затем просуммировать по всему объему:
. Затем просуммировать по всему объему: 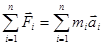 , или
, или  , где
, где  масса всего тела.
масса всего тела.
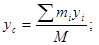
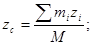
 .
. и
и  приложены к разным телам и поэтому не компенсируют друг друга.
приложены к разным телам и поэтому не компенсируют друг друга. .
. , определяемое правилом правого винта (буравчика), совпадает с направлением поступательного перемещения винта, если его ось совместить с осью вращения тела и поворачивать винт в направлении действия силы. На рис. 2.3. вектор
, определяемое правилом правого винта (буравчика), совпадает с направлением поступательного перемещения винта, если его ось совместить с осью вращения тела и поворачивать винт в направлении действия силы. На рис. 2.3. вектор  перпендикулярен к плоскости рисунка и направлен вдоль оси вращения О на нас.
перпендикулярен к плоскости рисунка и направлен вдоль оси вращения О на нас. = 0 (2.17)
= 0 (2.17) , проведенного из оси к точке, на импульс этой точки
, проведенного из оси к точке, на импульс этой точки 
 или
или  (см.2.41) (2.18)
(см.2.41) (2.18)
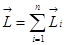 = const
= const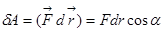 , (2.19)
, (2.19)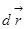 .
.
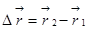 между точками 1 и 2:
между точками 1 и 2: , (2.20)
, (2.20) ,
, , (2.21)
, (2.21) - скорость движения.
- скорость движения. .
. .
. ,
, , получим dWk=mVdV.
, получим dWk=mVdV. (2.22)
(2.22)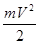 является функцией состояния системы. Она характеризует энергию, запасенную движущимся телом.
является функцией состояния системы. Она характеризует энергию, запасенную движущимся телом.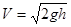 - (см. 2.3) и кинетическую энергию:
- (см. 2.3) и кинетическую энергию:
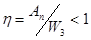
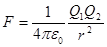 (3.1)
(3.1) (3.2)
(3.2)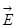 - напряженность. Напряженность электрического поля в данной точке численно равна отношению силы
- напряженность. Напряженность электрического поля в данной точке численно равна отношению силы 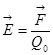 (3.3)
(3.3) .
. (3.4)
(3.4) , (3.32)
, (3.32) (3.40)
(3.40) , (3.41)
, (3.41) и
и 
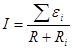 (3.42)
(3.42) . (3.49)
. (3.49) ,
,
 (3.50)
(3.50) (3.51)
(3.51)
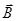 . Он направлен всегда по касательной к линии поля в любой точке.
. Он направлен всегда по касательной к линии поля в любой точке.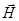
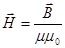 , (3.53)
, (3.53) - магнитная постоянная в СИ системе.
- магнитная постоянная в СИ системе. или Fл = QVB sin α, (3.54)
или Fл = QVB sin α, (3.54)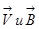 .
.
 перпендикулярен к вектору скорости
перпендикулярен к вектору скорости  , где m – масса частицы с зарядом Q.
, где m – масса частицы с зарядом Q. т.к. an = V2 / R (см.2.12)
т.к. an = V2 / R (см.2.12) .
. можно вычислить угловую скорость w вращения частицы, частоту ее вращения n или период Т.
можно вычислить угловую скорость w вращения частицы, частоту ее вращения n или период Т. и шагом
и шагом  и радиусом
и радиусом 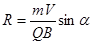 .
.
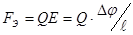 . При равенстве
. При равенстве  разделение зарядов прекращается, при этом Δφ=ℓVB. Ток в пластинке можно выразить через объемную плотность заряда Qn, площадь поперечного сечения ℓd проводника, скорость заряда V, т.е. I= Q nℓdV, откуда:
разделение зарядов прекращается, при этом Δφ=ℓVB. Ток в пластинке можно выразить через объемную плотность заряда Qn, площадь поперечного сечения ℓd проводника, скорость заряда V, т.е. I= Q nℓdV, откуда: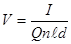
 , (3.55)
, (3.55) или
или  , (3.56)
, (3.56) - в ладонь, четыре пальца – ток, большой палец – сила
- в ладонь, четыре пальца – ток, большой палец – сила  (рис.3.13)
(рис.3.13)
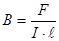 ,
,
 (3.57)
(3.57) -единичный вектор нормали к плоскости контура.
-единичный вектор нормали к плоскости контура.
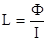 . Индуктивность контура зависит:
. Индуктивность контура зависит: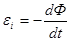 . Возникновение Э.Д.С. индукции в контуре вследствие изменения силы тока в самом контуре называется явлением самоиндукции. Величина Э.Д.С. самоиндукции:
. Возникновение Э.Д.С. индукции в контуре вследствие изменения силы тока в самом контуре называется явлением самоиндукции. Величина Э.Д.С. самоиндукции: (3.73)
(3.73) , (3.74)
, (3.74)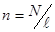 );
);
 ;
; .
. .
.
 (3.75)
(3.75) (см. формулу 3.74), а ток
(см. формулу 3.74), а ток 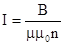 (см. формулу 3.65). Тогда уравнение (3.75) можно переписать:
(см. формулу 3.65). Тогда уравнение (3.75) можно переписать: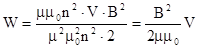 ,
,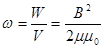 (3.76)
(3.76) или
или  . (3.77)
. (3.77) одного направления с внешним полем
одного направления с внешним полем  . Типичными парамагнетиками являются щелочные и щелочно - земельные металлы, кислород О2, окись азота и другие вещества – т.е. вещества, у которых атомы имеют собственный магнитный момент (3.24);
. Типичными парамагнетиками являются щелочные и щелочно - земельные металлы, кислород О2, окись азота и другие вещества – т.е. вещества, у которых атомы имеют собственный магнитный момент (3.24);


