
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логарифмический декремент затуханияСодержание книги
Поиск на нашем сайте
где τ -время релаксации (время, в течение которого амплитуда колебаний уменьшается в е раз); N-число колебаний за время τ. Логарифмический декремент
При затухающих колебаниях энергия системы расходуется на преодоление сопротивления среды. Если восполнять эту убыль энергии, то колебания станут незатухающими. Пополнение энергии может осуществляться за счет периодических толчков извне в такт с собственной частотой системы, тогда достигается механический резонанс. Особый технический интерес представляют устройства, имеющие возможность самой колеблющейся системе управлять этим процессом (анкерный механизм часов, ламповый генератор и др.). Такие системы называются автоколебательными. В электрическом колебательном контуре при R≠0 колебания также будут затухающими, и описываются уравнением (4.8). Обозначая через
решением его будет где частота Добротность контура при этом:
Вынужденные колебания возникают в системе под действием внешней периодически меняющейся силы. Рассмотрим это на примере электрического колебательного контура, в котором роль вынуждающей силы будет играть внешняя ЭДС периодически изменяющаяся по гармоническому закону
Общее решение неоднородного уравнения (4.14) позволяет для установившегося режима колебаний получить для тока в контуре:
где При постоянном R амплитуда тока I0 будет максимальна при
Рис. 4.5
Изменение амплитуды колебаний в системе в результате периодического изменения какого-либо параметра системы (R, L или С) называют параметрическим резонансом. Ангармонические колебания До этого мы рассматривали процессы на примерах гармонических или классических осцилляторов, совершающих колебания около положения равновесия. В положении равновесия потенциальная энергия системы П имеет минимум. Если отклонения от положения равновесия малы, то при разложении функции П(х) по степеням достаточно оставить первый член разложения (например
Волновые процессы
Если на каком-либо участке сплошной упругой среды возбудить гармоническое колебание, то оно будет передаваться соседним участкам этой среды, от них в свою очередь другим участкам и т.д. Такой процесс называется волновым процессом. Различают поперечные и продольные волны. Волна называется поперечной, если частицы среды колеблются перпендикулярно направлению ее распространения, и продольной, если они колеблются вдоль этого направления. Продольные волны могут распространяться в твердых, жидких и газообразных телах. Поперечные волны распространяются лишь в твердых телах. Примером поперечных волн являются волны, возбуждаемые при колебаниях струны, примером продольных - звуковые волны. Смещение частиц среды в поперечной волне показано на рис.4.6.
Рис. 4.6
Важно отметить, что сами частицы среды не переносятся волной, они лишь колеблются около положения равновесия. Наименьшее расстояние между двумя частицами, колеблющимися в одинаковой фазе, называется длиной волны λ (см. рис.4.6). λ - расстояние, на которое распространяется волна за время, равное периоду Т, т.е. λ = vТ, (4.15) где v-скорость волны. Скорость распространения волны определяется упругими свойствами среды и ее плотностью ρ: а) для продольных волн б) для поперечных волн Уравнение волны. Бегущей волной называется волна, которая переносит энергию. Перенос энергии характеризуется вектором плотности ω потока энергии – вектором Умова (см. также раздел 3.5): Представим себе волну, бегущую вдоль оси у (рис.4.6) х=А соs ωt Обозначим время, в течение, которого колебания среды достинут любой произвольной точки В, через
где V-фазовая скорость (скорость распространения колебаний в среде). Уравнение (4.16) будет уравнением плоской бегущей волны. Учитывая, что
где В общем случае уравнение плоской монохроматической волны, распространяющейся вдоль оси у, будет:
где φ0-начальная фаза колебаний. Для двух точек волны, лежащих на расстоянии Δу друг от друга разность фаз будет:
где Δ=Δу - разность хода волн. Если Δу=λ, то точки колеблются с разностью фаз Δφ=2π. Если Δу= λ/2, то разность фаз Δφ= π (точки колеблются в противофазах). Звуковыми называются механические волны, распространяющиеся в упругой среде и воспринимаемые человеком. Соответствующие им частоты лежат в диапазоне от 16 до 20·103 Гц. Волны с частотой меньше 16 Гц называются инфразвуковыми, а с частотой больше 20 кГц - ультразвуковыми. Звуковые волны на границе двух сред могут преломляться и отражаться (эхо, эхолокация, ультразвуковая дефектоскопия, УЗИ и т.д.). Сила звука определяется энергией, переносимой звуковой волной через единичную площадку в единицу времени (полная энергия пропорциональна квадрату амплитуды см. раздел 4.2). Громкость звука, связанная с его интенсивностью, измеряется в децибелах (дБ). В зависимости от акустического спектра различают тембры звуков и высоты. Плоские электромагнитные волны рассмотрены в разделе 3.5.
Интерференция волн
Волны от точечного источника распространяются во все стороны (сферические волны). Геометрическое место точек, до которых к некоторому моменту времени дошло колебание, называется фронтом волны. Совокупность точек, колеблющихся в одинаковых фазах, образует волновую поверхность. Волны обладают принципом суперпозиции, т.е. если в среде одновременно распространяются несколько волн, то они распространяются независимо друг от друга. Однако, в тех местах, где одни колебания накладываются на другие колебания, их амплитуды векторно складываются (см. рис.4.2). Наблюдается интерференция, в результате которой колебания в одних местах усиливаются, в других ослабляются. Особый интерес представляет тот случай, когда источники испускают волны с одинаковой частотой ω (такие волны называются монохроматическими), одинакового направления и с постоянной во времени разностью фаз Δφ. Волны с одинаковой частотой ω и постоянной разностью фаз называются когерентными. Вообще реальная волна, излучаемая в течение ограниченного промежутка времени и охватывающая ограниченную область распространения, не является монохроматической. Спектр ее частот имеет конечную ширину
|
|||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 724; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

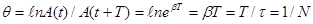 ,
, величина постоянная для данной системы. Системы характеризуются также добротностью:
величина постоянная для данной системы. Системы характеризуются также добротностью: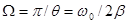
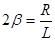 и
и 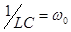 , получим для контура дифференциальное уравнение второго порядка:
, получим для контура дифференциальное уравнение второго порядка: , (4.13)
, (4.13)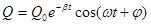 ,
,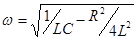 меньше собственной
меньше собственной 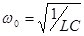 .
.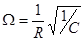
 . Тогда уравнение (4.13) запишется:
. Тогда уравнение (4.13) запишется: (4.14)
(4.14)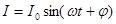 ,
,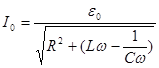 и
и 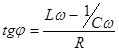 .
.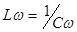 . Тогда
. Тогда 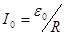 и ω=ω0. Наблюдается явление резонанса. Зависимость амплитуды вынужденных колебаний I0 от частоты ω вынуждающей силы и коэффициента затухания β показана на рис.4.5.
и ω=ω0. Наблюдается явление резонанса. Зависимость амплитуды вынужденных колебаний I0 от частоты ω вынуждающей силы и коэффициента затухания β показана на рис.4.5.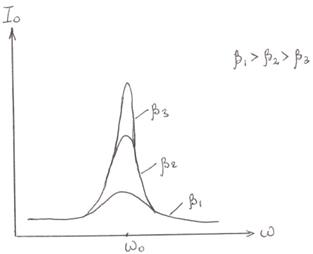
 ). Если необходим учет высших членов разложения, то осциллятор будет не гармоническим (ангармоническим). Его свойства нельзя описать линейным уравнением типа (4.4).
). Если необходим учет высших членов разложения, то осциллятор будет не гармоническим (ангармоническим). Его свойства нельзя описать линейным уравнением типа (4.4).
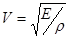 , где Е -модуль Юнга.
, где Е -модуль Юнга. , где G -модуль сдвига.
, где G -модуль сдвига. .
.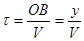 . Колебания этой точки будут гармоническими, но они отстают от колебаний точки О на время τ:
. Колебания этой точки будут гармоническими, но они отстают от колебаний точки О на время τ: , (4.16)
, (4.16)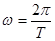 и ТV=λ, это уравнение можно переписать:
и ТV=λ, это уравнение можно переписать: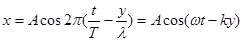 , (4.17)
, (4.17) - волновое число.
- волновое число.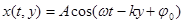 , (4.18)
, (4.18)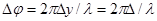 , (4.19)
, (4.19) . Такую волну можно лишь ограниченное время τ считать монохроматической с частотой ω. Величина τ называется временем когерентности. За время τ разность фаз колебаний изменяется на π. Волна с циклической частотой ω и фазовой скоростью V распространится за это время на расстояние d = V · τ, которое называется длиной когерентности. Например, для солнечного света, имеющего сплошной спектр в диапазоне частот от
. Такую волну можно лишь ограниченное время τ считать монохроматической с частотой ω. Величина τ называется временем когерентности. За время τ разность фаз колебаний изменяется на π. Волна с циклической частотой ω и фазовой скоростью V распространится за это время на расстояние d = V · τ, которое называется длиной когерентности. Например, для солнечного света, имеющего сплошной спектр в диапазоне частот от  до
до 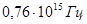
 и d~1мкм. Для лазеров непрерывного действия
и d~1мкм. Для лазеров непрерывного действия  и d~103м.
и d~103м.


