Происхождение квантовых корреляций

 

Чтобы закончить эту главу, давайте ответим на вопрос, как в математическом представлении квантовой физики описываются нелокальные корреляции. Уравнения-то работают очень хорошо, пусть и не объясняют, откуда появились эти нелокальные корреляции.

Согласно формально-математическому описанию, эти особенные корреляции возникают благодаря запутанности, а она, в свою очередь, описывается особым типом волны, которая распространяется в пространстве гораздо большей размерности, чем наше трехмерное. Пространство, в котором распространяются такие «волны», известно в физике как конфигурационное пространство, имеет количество измерений, зависящее от количества запутанных частиц, а конкретно – в три раза больше, чем это количество. В конфигурационном пространстве каждая точка представляет положения всех частиц, даже если они находятся на значительном удалении друг от друга. Таким образом, локальное событие в конфигурационном пространстве может задействовать очень далекие друг от друга частицы. Но мы, простые человеческие существа, не можем воспринять конфигурационное пространство, мы видим только тени происходящего в нем.

 

 

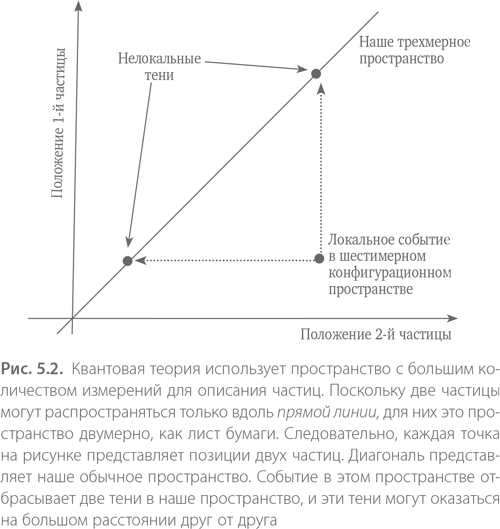
Каждая частица отбрасывает на наш трехмерный мир тень, соответствующую ее положению в нашем пространстве. Тени одной точки могут находиться далеко друг от друга в нашем пространстве, хотя их порождает одна конкретная точка в конфигурационном пространстве (см. рис. 5.2) Конечно, это достаточно странное объяснение, если его вообще можно назвать объяснением. Если так, то в определенном смысле реальность – это то, что происходит в другом, отличном от нашего мире, а то, что мы воспринимаем, – лишь смутные тени, как в аллегории Платона о пещере, которую он использовал много столетий назад для объяснения сложности познания «истинной реальности».

Это «объяснение» происхождения нелокальных квантовых корреляций кажется более математическим, нежели физическим. Действительно, трудно поверить, что истинная реальность происходит в пространстве, количество измерений в котором зависит от количества частиц, особенно если вспомнить, что это количество изменяется с течением времени. Короче говоря, математическая форма квантовой теории ничего не объясняет, а просто предоставляет собой способ вычисления. Некоторые физики вообще считают, что объяснять ничего не нужно: «Замолчите и считайте», – сказали бы они нам.

 

 

Глава 6

Эксперимент

 

В этой главе я познакомлю вас с экспериментом Белла – с тем, который мы провели в 1997 году в Женеве, или, если быть точнее, между деревнями Берне и Белльвю, которые находятся в десяти километрах друг от друга по прямой. В эксперименте использовалась оптоволоконная сеть швейцарского телекоммуникационного оператора Swisscom. Рис. 6.1 показывает схему этого эксперимента – первого эксперимента Белла, проведенного вне лаборатории.

 

 

Рождение пар фотонов

 

Начнем с главной части эксперимента, то есть с генерации запутанных фотонов. Атомы кристалла выстроены в исключительно равномерном порядке (имейте в виду, что кристалл, который мы использовали как источник для запутывания, не имеет никакого отношения к приборам Алисы и Боба). Каждый атом окружен облаком электронов. Если возбуждать атомы, воздействуя на них светом, электронные облака осциллируют вокруг ядер атомов. Если эти колебания несимметричны, то есть если электронные облака отклоняются от ядра в одном направлении легче, чем в другом, то мы имеем дело с нелинейным кристаллом. Причина такого названия вот в чем. Взаимодействие фотона с атомом переводит электронное облако в возбужденное состояние, и облако начинает осциллировать. Если оно колеблется симметрично, оно избавляется от возбуждения, испуская фотон той же энергии, что и изначальный, в совершенно произвольном направлении. Это явление называется флюоресценцией. Если же вибрация асимметрична, то релаксация облака происходит с испусканием фотона другого цвета.

Но цвет фотона определяет его энергию, а один из основных физических законов гласит, что энергия сохраняется. А значит, приведенное выше описание с неизбежностью неполно. Тем не менее существуют нелинейные кристаллы, которые, когда их освещают инфракрасным светом, излучают красивый зеленый свет. Этот физический механизм используется в зеленых лазерных указках, которые вы наверняка видели на презентациях в последние годы. Объясняется это так: нужно два низкоэнергетичных фотона из инфракрасной части спектра, чтобы создать один высокоэнергетичный фотон из зеленой области. Интенсивность этого зеленого света равна квадрату интенсивности инфракрасного[42], отсюда слово «нелинейный» в названии. Таким образом, нелинейный кристалл может изменять цвет светового луча. На уровне фотонов в этом процессе обязательно участвуют несколько фотонов низких энергий.

Законы физики работают и в обратном направлении. Это означает, что если некий элементарный процесс может идти в одном направлении, то должен быть возможен и обратный процесс. Следовательно, должна существовать возможность послать зеленый фотон в нелинейный кристалл и получить два инфракрасных фотона. И это будет процесс образования фотонных пар[43].

 

Создание запутанности

 

Осталось понять, почему эти фотоны запутаны. Чтобы это понять, вспомним, что квантовые частицы вроде фотонов обычно имеют неопределимые физические характеристики (положение в пространстве, скорость, энергия и т. д.). К примеру, фотон обладает некоторой энергией, но эта энергия неопределима. В среднем энергия фотона может принимать то или иное значение, но с неопределимостью, которая может быть очень существенной. Дело не в том, что мы не можем точно определить энергию фотона, а в том, что эта неопределимость является неотъемлемым свойством фотона, который сам «не знает», какую энергию несет. Короче говоря, фотон не обладает неким точным значением энергии, а имеет целый спектр потенциально возможных значений (так же как позиция электрона в главе 5). Если мы очень точно измеряем энергию фотона, мы получаем случайный результат из целого спектра возможностей – истинно случайный, как мы говорили выше, результат. Следует понимать, что для воспроизведения истинной случайности, которая, как мы видели, необходима для победы в игре Белла, определенные физические величины не должны иметь точно определенных значений. Они должны быть неопределимыми и принимать точное значение лишь тогда, когда делается точное измерение. Какое точное значение? А вот это – уже квантовая случайность.

Как энергия, так и возраст фотона, а именно время, прошедшее с момента, когда он был испущен источником света, также может быть неопределим. Потенциальный возраст фотона может варьировать от нескольких миллиардных долей секунды вплоть до нескольких секунд, в зависимости от того, каким образом этот фотон был излучен. Знаменитое соотношение неопределенности Гейзенберга (см. справку 8) для фотонов гласит, что чем точнее определен возраст фотона, тем выше неопределимость его энергии. И наоборот, чем точнее мы знаем его энергию, тем выше неопределимость его возраста.

Но вернемся к нелинейным кристаллам и парам фотонов, которые они производят. Представьте, что нелинейный кристалл возбуждается зеленым фотоном с очень точно определенным значением энергии, то есть с очень низкой неопределимостью энергии. Этот фотон превращается в два инфракрасных фотона, каждый из которых обладает неопределимой энергией, но при этом сумма этих энергий в точности равна энергии первоначального зеленого фотона. Мы получаем два инфракрасных фотона, каждый с неопределимой энергией, но сумма этих двух энергий определена очень точно.

Таким образом, энергии двух фотонов коррелируют. Если мы измерим эти энергии и обнаружим, что у одного из них значение энергии выше среднего, то значение энергии у другого обязательно будет ниже среднего. Удивительное свойство нелокальности: энергия одного фотона, изначально неопределимая, может быть определена в результате измерения энергии другого фотона.

Но этого все еще недостаточно. Чтобы играть в игру Белла, мы должны иметь возможность выбора по меньшей мере из двух типов измерений – они будут соответствовать двум положениям джойстика. Так как мы очень точно знаем энергию исходного зеленого фотона, то, в соответствии с принципом неопределенности Гейзенберга, его возраст соответственно неопределим. А что мы можем сказать о паре инфракрасных фотонов? Поскольку их энергии неопределимы, их возраст мы можем определить довольно точно – в действительности даже более точно, чем возраст зеленого фотона.

Но может ли один из инфракрасных фотонов быть старше другого? Ответ: не может, ведь так могло получиться лишь в том случае, если бы этот фотон возник в кристалле раньше другого. Но если бы один из инфракрасных фотонов появился раньше другого, то это означало бы, что в короткий интервал времени между их появлениями не действовал закон сохранения энергии, а это невозможно. Два инфракрасных фотона должны появиться одновременно, ровно в тот момент, когда распался зеленый фотон. Так в какой именно момент появляются инфракрасные фотоны? Ответ таков: момент появления двух инфракрасных фотонов неопределим, так же как и возраст зеленого фотона.

Итак, два инфракрасных фотона имеют одинаковый возраст, но этот возраст неопределим. Если мы измерим возраст одного из них, мы получим истинно случайный результат. Но с этого момента возраст второго фотона становится определенным. Это и есть вторая квантовая корреляция, которая необходима, чтобы играть и выиграть[44].

Как только наши фотоны прибыли в места назначения – один в прибор Алисы, другой в прибор Боба, в идеальной ситуации их нужно сохранить в памяти. Разработки такой памяти, называемой квантовой, все еще ведутся в исследовательских лабораториях. В настоящее время эта технология не очень эффективна, и фотон хранится лишь крошечную долю секунды. Поэтому мы попросим Алису и Боба сделать выбор чуть раньше, чем прибудут фотоны. Таким образом, измерение произойдет мгновенно в момент прибытия. Положение джойстика определяет, что будет измерено – энергия или возраст (энергия или время, сказали бы ученые). В итоге каждый прибор покажет результат измерения. В принципе в приборах друзей могло бы храниться достаточное количество фотонов для игры, как она описана в главе 2 (и технология очень скоро даст такую возможность). Кристаллы в центре двух приборов – это и есть квантовые запоминающие устройства, которые способны хранить несколько сотен запутанных фотонов, как квантовые кристаллы памяти, которые мы сейчас разрабатываем в Женеве (однако продолжительность хранения и эффективность необходимо будет значительно увеличить).