
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Потенциал электрического поляСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
 Помимо напряженности электрическое поле характеризуется еще одной важной физической величиной – потенциалом. Помимо напряженности электрическое поле характеризуется еще одной важной физической величиной – потенциалом.
Рассмотрим перемещение заряда q в поле другого точечного заряда q 0 из точки 1 в точку 2 (рис. 6.3). Работа силы F на элементарном перемещении dl определяется соотношением
но
Для вычисления работы перемещения заряда из точки 1 в точку 2 по произвольному пути 1–2 проинтегрируем (6.6) в пределах от r 1 до r 2 , получим
Из выражения (6.7) следует, что работа перемещения электрического заряда не зависит от формы пути, по которому перемещается заряд, а зависит только от начальной и конечной точек. Если заряд q, перемещаясь в электрическом поле, возвращается в исходную точку (r 2 = r 1), то работа перемещения заряда по замкнутому пути в электростатическом поле равна нулю. Поля, обладающие указанным свойством, называются потенциальными. Найдем отношение работы перемещения заряда к величине этого заряда:
Эта величина не зависит от величины перемещаемого заряда и от пути, по которому он перемещается, и поэтому служит характеристикой поля, созданного зарядом q 0, и называется разностью потенциалов или электрическим напряжением. Разность потенциалов двух точек 1 и 2 электрического поля измеряется работой, совершаемой полем при перемещении единичного положительного заряда между этими точками. Следует подчеркнуть, что разность потенциалов имеет смысл характеристики поля потому, что работа перемещения заряда не зависит от формы пути. Действительно, если бы работа перемещения заряда зависела от пути, то при перемещении одного и того же заряда между теми же самыми точками поля, это отношение A / q не являлось бы однозначной характеристикой этих точек поля. Если выбрать какую-либо точку пространства в качестве начальной точки (точки отсчета), то любой точке можно сопоставить разность потенциалов относительно этой начальной точки. Для случая поля точечного заряда наиболее простое математическое выражение для потенциала получается, если в качестве начальной выбрать любую точку, удаленную на бесконечность. Тогда работа перемещения положительного заряда q из бесконечности в данную точку поля, созданного другим точечным зарядом q 0, будет равна
Отношение работы перемещения положительного заряда из бесконечности в данную точку поля к величине этого заряда (работа по перемещению единичного заряда) называется потенциалом данной точки поля:
Знак минус в этом выражении означает, что в данном случае работа совершается внешними силами против сил поля. Очевидно, что напряжение U между произвольными точками 1 и 2 электрического поля и потенциалы этих точек связаны простым соотношением
Для поля точечного заряда
Потенциал любой точки поля, созданного положительным зарядом – положителен и убывает до нуля по мере удаления от заряда. Напротив – потенциал поля, созданного отрицательным зарядом, – отрицательная величина и растет до нуля по мере удаления от заряда.
Работу перемещения заряда можно выразить через разность потенциалов
Отсюда следует, что работа перемещения заряда по эквипотенциальной поверхности равна нулю. Это значит, что сила, действующая на заряд, а следовательно, и вектор напряженности поля Е направлены перпендикулярно эквипотенциальной поверхности. Используя эквипотенциальные поверхности, можно также дать графическое изображение электрического поля. Результаты, полученные для поля точечного заряда, легко распространить на поля, созданные любым числом точечных зарядов, а так как любое заряженное тело можно представить как совокупность точечных зарядов, то и на поле, созданное любым заряженным телом. Поля точечных зарядов в соответствии с принципом суперпозиции, накладываясь друг на друга, не влияют друг на друга. Поэтому потенциал поля любого числа зарядов будет равен алгебраической сумме потенциалов полей, созданных отдельными зарядами, т. е.:
Таким образом, все вышеизложенное в отношении понятия потенциала справедливо и для поля, созданного заряженным телом любой формы, а величину потенциала, в принципе, можно вычислить по формуле (6.14).
|
|||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 504; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.186.233 (0.006 с.) |


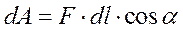 , (6.5)
, (6.5) , значит
, значит 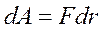 . Подставим сюда вместо силы ее значение из закона Кулона, получим:
. Подставим сюда вместо силы ее значение из закона Кулона, получим: . (6.6)
. (6.6) . (6.7)
. (6.7) . (6.8)
. (6.8) . (6.9)
. (6.9) . (6.10)
. (6.10) . (6.11)
. (6.11) . (6.12)
. (6.12) Из выражения для потенциала (6.12) следует, что потенциал любой точки сферической поверхности S c центром в точке расположения заряда одинаков (рис. 6.4). Такие поверхности называются поверхностями равного потенциала или эквипотенциальными поверхностями.
Из выражения для потенциала (6.12) следует, что потенциал любой точки сферической поверхности S c центром в точке расположения заряда одинаков (рис. 6.4). Такие поверхности называются поверхностями равного потенциала или эквипотенциальными поверхностями.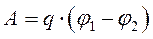 . (6.13)
. (6.13) . (6.14)
. (6.14)


