
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложение взаимно перпендикулярных гармонических колебанийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы: изучить форму траектории материальной точки, участвующей в двух взаимно перпендикулярных колебаниях. Определить разность фаз складываемых колебаний из вида траектории результирующего движения. Оборудование: песочный маятник, секундомер, линейка, лист бумаги, песок.
Теория метода Простейшим видом колебательных движений является гармоническое колебание. Оно возникает в том случае, если на тело, выведенное из положения равновесия, действует сила, направленная всегда к положению равновесия, а по величине пропорциональная смещению тела от положения равновесия. Таким образом, можно написать
где F – сила, под действием которой тело совершает гармоническое колебание; s – смещение тела от положения равновесия; k – некоторый постоянный коэффициент. Это выражение можно написать и в таком виде
где m – масса колеблющегося тела;
которая описывает гармоническое колебание величины s, где а – амплитуда колебания; ω – круговая (циклическая) частота; φ– начальная фаза колебания в момент времени t = 0; (ωt + φ)–фаза колебания в момент времени t. Фаза колебания определяет значение колеблющейся величины в данный момент времени. Так как синус изменяется в пределах от +1 до –1, то s может принимать значения от +а до – а. Циклическая частота связана с периодом колебаний соотношением При изучении колебательных движений большой интерес представляют вопросы, связанные со сложением колебаний. Ограничимся анализом сложения взаимно перпендикулярных гармонических колебаний. Рассмотрим систему, обладающую двумя степенями свободы, т. е. такую систему, для задания положения которой необходимы две величины. Примером может служить математический маятник (тяжелое тело небольших размеров, подвешенное на длинной невесомой нити), который может совершать колебания одновременно в двух взаимно перпендикулярных плоскостях. Частоты этих колебаний будут одинаковы и будут зависеть только от длины нити l и ускорения свободного падения g. Пусть начальная фаза первого колебания равна нулю, тогда уравнения колебаний запишутся следующим образом:
где а, b – амплитуды колебаний; φ – разность фаз обоих колебаний; ω – частота колебаний. Выражения (3.1) представляют собой заданное в параметрической форме уравнение траектории, по которой движется точка, участвующая в обоих колебаниях. Чтобы получить уравнение траектории в обычном виде, нужно исключить из уравнений (3.1) параметр t. Из первого уравнения следует, что
Следовательно
Распишем косинус во втором уравнении системы (3.1) по формуле для косинуса суммы, подставляя при этом вместо cos ωt и sin ωt их значения (3.2) и (3.3). В результате получим
Перенося слагаемое
Исследуем форму траектории в некоторых частных случаях. 1. Разность фаз φ = 0. В этом случае уравнение (3.4) принимает вид
Колеблющаяся точка перемещается по этой прямой, причем расстояние ее от начала координат равно Подставляя выражения (3.1) для х и у и учитывая, что φ = 0, получим закон, по которому r изменяется со временем:
где 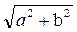 –амплитуда результирующего колебания (рис. 3.2, а). –амплитуда результирующего колебания (рис. 3.2, а).
2. Разность фаз φ = ±π. Тогда из уравнения (3.4) следует, что 3. При
т. е. в уравнение эллипса, приведенного к координатным осям, причем полуоси эллипса равны соответствующим амплитудам колебаний (рис. 3.2, в). При равенстве амплитуд а и b эллипс вырождается в окружность (рис. 3.2, г). Случаи
На рис. 3.3 изображены фигуры Лиссажу (траектории результирующего колебания при различном соотношении частот и разности фаз между складываемыми колебаниями во взаимно перпендикулярных плоскостях).
«Песочный» маятник, используемый в лабораторной работе, представляет собой математический маятник. Для такого маятника с достаточной точностью выполняется формула
где Т – период колебаний математического маятника; l – его длина; g – ускорение силы тяжести. Математический маятник совершает гармонические колебания, если угол отклонения нити от положения равновесия не превышает ~8°. «Песочный маятник» состоит из тяжелого тела М с воронкой для песка, подвешенного на двух нитях (бифилярный подвес) к раме с перекладиной (рис. 3.4, а). С помощью муфты С, передвигаемой вдоль нити, можно реализовать различное соотношение частот между складывающимися колебаниями. При этом одно из колебаний совершается относительно точки Д, а второе – относительно точки С. Колеблющийся маятник совершает движения, которые можно рассматривать как результат сложения колебаний по двум взаимно перпендикулярным направлениям. Если, насыпав песок в воронку, менять соотношения периодов складываемых колебаний (перемещением муфты), то можно наблюдать различные фигуры Лиссажу – траектории, описываемые маятником.
Примечание. Воронку следует располагать в непосредственной близости от листа бумаги, песок сыпать в воронку нужно перед наблюдением, после проведения всех дополнительных работ. Измерения Задание 1. Исследуйте форму траектории суммарного колебания при произвольной разности фаз φ и одинаковой частоте складываемых взаимно перпендикулярных колебаний. Определите параметры колебаний (амплитуды а и b, разность фаз φ и частоту ω). Настройте песочный маятник так, чтобы складываемые колебания имели одинаковые частоты (w1 = w2), для чего нужно закрепить муфту С за крючок Д перекладины. Определить период колебаний Т и рассчитать частоту складываемых колебаний Для исследования траектории следует положить под маятник лист бумаги, отметить на нем проекцию неподвижного маятника (точка О) и провести оси Ох и Оу. Насыпав песок в воронку, получить траекторию суммарного колебания, отводя маятник в направлении оси х (или у) и сообщая небольшой импульс в направлении оси у (или х). Найдите амплитуды а и b и разность фаз φ складываемых колебаний. Напишите уравнение колебательного движения. Данные измерений и вычислений занесите в табл. 3.1 Таблица 3.1
Задание 2. Исследуйте форму траектории суммарного колебания при разности фаз, равной 0, и отношении частот складываемых колебаний w1:w2 = 1:2. Определите параметры взаимно перпендикулярных колебаний (амплитуды а и b, отношение частот w1:w2, разность фаз φ). Напишите уравнение траектории суммарных колебаний. Выполнение задания следует начинать с расчета длин маятников, для которых отношение периодов (частот) их колебаний будет равно 2. Поместите на нитях муфту так, чтобы длины получившихся маятников удовлетворяли найденному условию. Проверьте правильность нахождения положения муфты непосредственным измерением периодов колебаний маятников. Если нужно, перемещением муфты добейтесь желаемого результата. Получите и зарисуйте траекторию колебаний и найдите необходимые параметры, характеризующие колебательный процесс. Данные измерений и вычислений занесите в табл. 3.2. Таблица 3.2
Литература 1. Сивухин, Д. В. Общий курс физики. Механика. В 3 т. Т. 1 / Д. В. Сивухин. М.: Высшая школа, 1989. 2. Гершензон, Е. М. Механика / Е. М. Гершензон, Н. Н. Малов, А. Н. Мансуров. М.: Академия, 2001.
Лабораторная работа № 4 Определение отношения теплоемкостей газов СP/СV методом Клемана и Дезорма
Цель работы: определить отношение CP/CV для воздуха, изучить адиабатический и другие процессы в газах. Приборы и принадлежности: стеклянный баллон, водяной манометр, осушитель, насос. Теория метода
Выделим в сосуде некоторое количество z воздуха (объем V1) и рассмотрим процессы, которые с ним происходят. Первое состояние характеризуется параметрами P1, V1, T1, где P1 = Р0 + rgh1. Откроем и быстро закроем кран К так, чтобы давление в баллоне сравнялось с атмосферным. Часть газа из баллона (но не из объема V1) выйдет через кран. Так как процесс расширения выбранного нами количества воздуха происходит быстро, а процесс теплообмена с окружающей средой, благодаря малой теплопроводности стенок баллона, идет медленно, этот процесс можно считать адиабатическим. Температура газа при этом уменьшается. Второе состояние характеризуется параметрами Р0, V2, Т. Далее за счет теплообмена с окружающей средой газ медленно нагревается до тех пор, пока его температура не сравняется с температурой окружающей среды. Разность уровней в манометре не перестанет меняться и станет равной h2. Третье состояние характеризуется параметрами Р2, V2, Т0, где Р2 = Р0 + rgh2. Разность давлений P1 – Р0 и P2 – Р1 во много раз меньше атмосферного давления. Действительно, атмосферному давлению соответствует высота водяного столба, примерно равная 103 см, а указанные разности не превышают 30 см. Поэтому для упрощения вычислений с этими разностями можно обращаться как с бесконечно малыми дифференциалами. То же относится и к изменению объема выделенной порции газа. Напишем первое начало термодинамики:
dQ = zCVdT + PdV, (4.1) где z – число молей газа.
Для адиабатического перехода из состояния 1 в состояние 2 dQ = 0, значит zCVdT + PdV = 0. (4.2)
Продифференцируем уравнение Менделеева-Клапейрона
PdV + VdP = zRdT.
Найдем dT и подставим в формулу (4.2). Получим
откуда
где Это уравнение адиабатического процесса в дифференциальной форме, его решение дает формула Пуассона. Учитывая сказанное ранее о разностях давлений и объемов, окончательно запишем:
gР(V2 – V1) +V(P0 – P1) = 0. (4.4)
В состояниях 1 и 3 температуры газа одинаковы, поэтому, как это следует из уравнения Менделеева-Клапейрона, Р1V1 = Р2V2, т. е. PV = const. Продифференцируем это выражение PdV + VdP = 0 и перейдем к разностям объемов и давлений Р(V2 – V1) +V(P2 – P1) = 0. (4.5)
Решая совместно уравнения (4.3) и (4.5) относительно g, получим уравнение
В результате получается расчетная формула для определения СР/СV:
Порядок выполнения работы 1. Накачать в сосуд воздух. После установления равновесия измерить разность уровней воды в манометре h1. 2. Открыть и быстро закрыть кран К. После установления равновесия измерить разность уровней в манометре h2. 3. Проделать 10 измерений, вычислить среднее значение СР/СV, абсолютную и относительную погрешности. Контрольные вопросы 1. Какие процессы имеют место в эксперименте? 2. Почему СР > СV? 3. Как теоретически определить СР/СV? 4. Почему экспериментальные результаты систематически меньше теоретически вычисленной величины? Литература 1. Яковлев, В.Ф. Курс физики. Теплота и молекулярная физика / В.Ф. Яковлев. М., 1976, §§7, 19–23, 37. 2. Сивухин, Д. В. Курс физики. Т. 2 / Д. В. Сивухин. М.: «Наука», 1986, §§20–22.
Лабораторная работа № 5
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 904; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.214.226 (0.007 с.) |

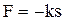 ,
,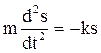 ,
, – его ускорение, которое выражено в дифференциальной форме, так как в колебательном движении оно является величиной переменной. Решением этого уравнения является функция синуса (или косинуса)
– его ускорение, которое выражено в дифференциальной форме, так как в колебательном движении оно является величиной переменной. Решением этого уравнения является функция синуса (или косинуса) ,
,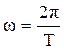 , где Т – период колебаний, т. е. промежуток времени, за который фаза колебаний получает приращение 2π.
, где Т – период колебаний, т. е. промежуток времени, за который фаза колебаний получает приращение 2π.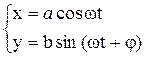 , (3.1)
, (3.1)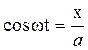 . (3.2)
. (3.2)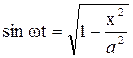 . (3.3)
. (3.3) .
.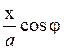 влево и возводя в квадрат полученное выражение, получим:
влево и возводя в квадрат полученное выражение, получим: . (3.4)
. (3.4)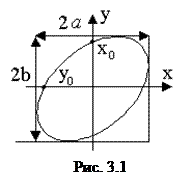 Как известно из аналитической геометрии, уравнение (3.4) есть уравнение эллипса, оси которого ориентированы относительно координатных осей х и у произвольно. Ориентация эллипса и величина его полуосей зависит от амплитуд а и b и разности фаз φ. Все эллипсы вписываются в прямоугольник со сторонами 2 а и 2b (рис. 3.1) Разность фаз складываемых колебаний можно найти, подставив х = 0 в уравнение (10.4). В этом случае
Как известно из аналитической геометрии, уравнение (3.4) есть уравнение эллипса, оси которого ориентированы относительно координатных осей х и у произвольно. Ориентация эллипса и величина его полуосей зависит от амплитуд а и b и разности фаз φ. Все эллипсы вписываются в прямоугольник со сторонами 2 а и 2b (рис. 3.1) Разность фаз складываемых колебаний можно найти, подставив х = 0 в уравнение (10.4). В этом случае и
и 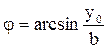 .
.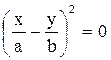 , откуда получается уравнение прямой
, откуда получается уравнение прямой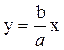 . (3.5)
. (3.5) .
.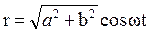 , (3.6)
, (3.6)
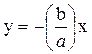 . (рис. 3.2, б).
. (рис. 3.2, б).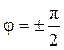 уравнение (3.4) переходит в
уравнение (3.4) переходит в ,
, и
и 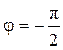 отличаются направлением движения по эллипсу или по окружности. Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектория движения имеет вид довольно сложных кривых, называемых фигурами Лиссажу. Уравнения колебаний имеют вид
отличаются направлением движения по эллипсу или по окружности. Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектория движения имеет вид довольно сложных кривых, называемых фигурами Лиссажу. Уравнения колебаний имеют вид .
.
 ,
,
 .
. Стеклянный баллон (рис. 4.1) наполнен воздухом при атмосферном давлении. С помощью насоса в баллон через осушитель накачивается дополнительная порция воздуха, пока разность уровней воды в манометре М не составит 25–30 см. Кран K закрывается и через некоторое время температура газа в баллоне сравняется с температурой окружающей среды, разность уровней перестанет меняться и будет равной h1.
Стеклянный баллон (рис. 4.1) наполнен воздухом при атмосферном давлении. С помощью насоса в баллон через осушитель накачивается дополнительная порция воздуха, пока разность уровней воды в манометре М не составит 25–30 см. Кран K закрывается и через некоторое время температура газа в баллоне сравняется с температурой окружающей среды, разность уровней перестанет меняться и будет равной h1.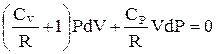 ,
,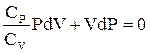 , (4.3)
, (4.3)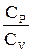 – показатель адиабаты.
– показатель адиабаты. .
.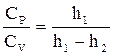 . (4.6)
. (4.6)


