
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электростатика. Магнетизм. Колебания и волныСодержание книги
Поиск на нашем сайте Часть II
Электростатика. Магнетизм. Колебания и волны
Утверждено Редакционно-издательским советом университета в качестве учебного пособия
Новосибирск УДК 53(075.8) Д 138
Рецензенты: А.А. Харьков, канд. физ.-мат. наук, доц. А.В. Баранов, канд. физ.-мат. наук, доц.
Работа подготовлена на кафедре общей физики
Давыдков В.В.
Д 138 Курс общей физики для студентов ИДО: Учеб. пособие: 2-е изд., испр. – Новосибирск: Изд-во НГТУ, 2005. Ч. II. – 158 с.
ISBN 5-7782-0538-4
В пособии изложен теоретический материал по электростатике и магнетизму, колебаниям и волнам. Учебное пособие соответствует программе изучения курса общей физики, рассчитанной на три учебных семестра. Курс лекций по общей физике предназначен для студентов института дистанционного образования, изучающих вторую часть курса физики.
УДК 53 (075.8) ISBN 5-7782-0538-4 Ó Давыдков В.В., 2005 Ó Новосибирский государственный
Электростатика
Электростатика – раздел физики, изучающий взаимодействие неподвижных зарядов.
Электрические заряды. Закон Кулона
Шарль Кулон в XVIII в. за-нимался изучением взаимо-дейдействия электрических за-рядов. В качестве зарядов он ис-пользовал наэлектризованные шарики, размеры которых были малы по сравнению с расстоя-нием между ними. Такие заряды называются точечными. В результате серии экспериментов он обнаружил, что сила электростатического взаимодействия двух точечных зарядов прямо пропорциональна произведению величин зарядов, обратно пропорциональна квадрату расстояния между заря-дами и направлена вдоль прямой, соединяющей точечные заряды
где F 12 – сила, действующая на первый заряд со стороны второго; q 1, q 2 – величины первого и второго зарядов; r 12 – расстояние между зарядами; r 12 – вектор, соединяющий первый заряд Закон Кулона записан в форме, соответствующей международной системе единиц СИ. Это значит, что величина зарядов измеряется в кулонах (обозначается Кл), расстояние –
Электрическое поле. Напряжённость Электрического поля
В соответствии с законом Кулона, электрические заряды действуют друг на друга при любом расстоянии между ними. Это объясняется тем, что каждый заряд создаёт вокруг себя электрическое поле. Любой другой заряд, помещённый в электрическое поле, взаимодействует с ним, вследствие чего на заряд действует кулоновская сила. Величина кулоновской силы, действующей на заряд, зависит от электрического поля. Чем сильнее поле, тем больше сила. Но как количественно охарактеризовать электрическое поле? Ввести такую характеристику можно следующим образом. Пусть в некоторую точку электрического поля мы поочерёдно помещаем разные заряды и измеряем силу, действующую на них:
Здесь F 1 – сила, действовавшая на заряд q 1, помещённый в интересующую нас точку поля, F 2 – сила, действовавшая на заряд q 2, и т. д. Поскольку заряды разные, то и силы будут различны по величине. Но оказывается, что отношение силы, действующей на данный заряд, к его величине не зависит от величины этого заряда
____________________________
* Размерность электрической постоянной часто записывают в ином виде: Кл2/(Н×м2) = Ф/м; здесь Ф – размерность электрической емкости (читается – «фарада»).
Величина Е, равная отношению силы, действующей на заряд, помещённый в заданную точку электрического поля (пробный заряд), к величине этого заряда называется напряжённостью
Можно также сказать, что напряжённость численно равна силе, действующей на единичный положительный пробный заряд. Напряжённость является векторной величиной. Направление вектора напряжённости совпадает с направлением силы, действующей на положительный пробный заряд. Если в качестве пробного используется отрицательный заряд, то вектор напряжённости будет противоположен направлению силы, действующей на отрицательный пробный заряд. Размерность напряжённости, как это видно из определения, [E] = Н/Кл = В/м*. Напряжённость является силовой характеристикой элект-рического поля**, поскольку определяет силу, действующую на заряд, помещённый в данную точку электрического поля. Следует обратить внимание на одну важную деталь. Пробный заряд должен быть малым по величине. Но можно ли считать малым заряд, например в 0,1 Кл? Или 0,01 Кл? Критерием малости пробного заряда является влияние этого заряда на заряды, создающие исследуемое электрическое поле. Пробный заряд мал, если его появление в электрическом поле не вызывает изменения положения зарядов, создающих элект-рическое поле. Найдём напряжённость поля, созданного точечным зарядом q. Для этого на расстоянии r от заряда q поместим пробный заряд q о. Тогда сила, действующая на пробный заряд, в соответствии с законом Кулона равна
_________________________
* Размерность В/м будет получена позже. ** В этом заключается физический смысл напряженности.
Отсюда напряжённость поля точечного заряда q равна
Таким образом, напряжённость поля, созданного точечным зарядом q в интересующей нас точке, прямо пропорциональна величине заряда, создающего поле, и обратно пропорциональна квадрату расстояния от заряда до интересующей нас точки. Полученное выражение позволяет рассчитать напряжённость электрического поля, созданного точечным зарядом, в любой его точке. Зная напряжённость электрического поля в нужной точке, легко рассчитать силу, которая будет действовать на заряд, помещённый в эту точку F = q E, где Е – напряжённость электрического поля в точке распо-ложения заряда q.
Принцип суперпозиции
Закон Кулона описывает взаимодействие двух точечных зарядов. Однако взаимодействовать одновременно могут и три, и более зарядов. Как описать взаимодействие в этом случае? Экспериментально доказано, что взаимодействие двух точечных зарядов не зависит от наличия третьего заряда. Отсюда следует, что если необходимо найти силу F, действующую на заряд q со стороны зарядов q 1, q 2, q 3... qn, достаточно рассчитать силу F 1, действующую на заряд q со стороны заряда q 1, F 2 – со стороны заряда q 2, и т. д., а затем найти их равнодействующую F = F 1 + F2 + F 3 +...+ Fn Другими словами – результат взаимодействия заряда с несколькими другими зарядами является результатом наложения (суперпозиции) взаимодействий заряда q с каждым из зарядов Поэтому сила, действующая на заряд со стороны нескольких других зарядов, равна векторной сумме всех сил, действующих на интересующий нас заряд со стороны каждого из окружающих его зарядов в отдельности. Это выражение представляет собой одну из возможных формулировок принципа суперпозиции. Выражение для расчёта силы F можно записать в следующем виде:
= где Е 1 – напряжённость поля, созданного зарядом q 1 в точке расположения заряда q, Е 2 – напряжённость поля, созданного там же вторым зарядом, Е i – напряжённость поля, созданного i – м зарядом в точке расположения заряда q. Сокращая q, получаем
Таким образом, напряжённость поля, созданного не-сколькими зарядами в интересующей нас точке, равна век-торной сумме напряжённостей, созданных каждым из заря-дов в этой точке. Данное выражение представляет собой принцип супер-позиции для вектора напряжённости электрического поля. В ряде случаев поле создаётся не точечными, а так называемыми распределёнными зарядами. Например, поле, соз-данное заряженной нитью. В таких ситуациях распределённый заряд делят на малые порции dqi, после чего рассчитывают напряжённость поля, используя принцип суперпозиции: Учитывая, что dqi является малой величиной, суммирование целесообразно заменить интегрированием
Величина dq может быть выражена следующим образом: – если заряд распределён по линии, то dq = t dl, где t – линейная плотность заряда (это заряд единицы длины заряженной нити: – если заряд распределён по поверхности, то dq = s ds, где s – поверхностная плотность заряда (это заряд единицы площади заряженной поверхности: – если заряд распределён по объёму, то dq = r dV, где r – объёмная плотность заряда (это заряд единицы объёма заряженного тела: Важно отметить, что принцип суперпозиции полей справедлив для сред, свойства которых не зависят от величины напряжённости электрического поля. Например, в вакууме поле, созданное несколькими зарядами, равно сумме полей, созданных каждым из зарядов в отдельности. Для сегнетоэлектриков это утверждение неверно, так как их электрические свойства очень сильно зависят от напряжённости поля в сегнетоэлектрике. Для большинства сред (газы, аморфные вещества, ряд кристаллических веществ) в слабых электрических полях прин-цип суперпозиции справедлив.
Поток вектора напряжённости
В ряде разделов курса общей физики рассматриваются векторные поля (например, электростатическое поле, магнитное поле).
Пусть в некоторой области пространства существует электрическое поле. Выберем в этом поле элементарную площадку ds. Пусть нормаль к этой площадке n образует угол a c вектором напряжённости электрического поля (модуль вектора n = 1). Потоком вектора напряжённости электрического поля через эту площадку называется величина, равная
где dФ – элементарный поток вектора напряжённости, Е – вектор напряжённости поля в пределах бесконечно малой площадки площадью d s. Произведение En является скалярным, поэтому поток вектора напряжённости является скалярной величиной. Иногда произведение n ds заменяют на вектор d s, который направлен перпендикулярно плоскости площадки; модуль вектора ds равен площади элементарной площадки. Поток напряжённости через конечную площадь s равен
В зависимости от величины угла между нормалью к площадке и вектором Е поток может быть положительным и отрицательным. Если угол между векторами Е и n острый, то поток положителен, если тупой – отрицателен. Обратите внимание на то, что направление вектора n выбирается перед решением задачи произвольно (перпендикуляр к поверхности можно направить в две взаимно противоположные стороны). Поэтому знак потока вектора напряжённости опреде-ляется выбором направления вектора n. Если поверхность замкнутая, поток вектора напряжённости равен
т. е. интеграл берётся по замкнутой поверхности s. В этом случае принято направлять вектор n наружу от поверхности. При этом поток через замкнутую поверхность положителен, если суммарный заряд, охваченный замкнутой поверхностью, положителен. Размерность потока вектора напряжённости [Ф]=В.м=Н.м2/Кл.
Теорема Гаусса
Теорема Гаусса – основная теорема электростатики. Она устанавливает связь между потоком вектора напряжённости через замкнутую поверхность и суммарным зарядом, охваченным этой поверхностью. Рассмотрим эту теорему. Пусть электрическое поле создано положительным точечным зарядом q. Найдём поток вектора напряжённости электрического поля через замкнутую поверхность, охватывающую этот заряд. В качестве поверхности выберем сферу радиуса r, центр которой совпадает с зарядом q. Будем считать, что векторы n во всех точках замкнутой поверхности направлены от центра сферы. Поскольку заряд, создающий поле, положителен и распо-ложен в центре сферы, постольку угол между вектором Е и вектором n во всех точках поверхности равен нулю.
Другими словами, в рассматриваемой ситуации скалярное произведение вектора напряжённости электростатического поля на вектор элементарной поверхности ра-вен произведению модулей этих век-торов. Напряжённость поля, созданного то-чечным зарядом, равна Поскольку заряд расположен в центре сферической по-верхности, расстояние от заряда до поверхности во всех её точках одинаково и равно r. Следовательно, модуль вектора напряжённости во всех точках сферической поверхности одинаков: E = const. Константу можно вынести за знак интеграла, поэтому поток вектора напряжённости через замкнутую поверхность в данном случае равен Интеграл от элементарных площадей поверхности s, взятый по всей поверхности, равен площади этой поверхности s. Таким образом, поток вектора напряжённости через замкнутую поверхность в данном случае равен Подставив выражение для расчёта напряжённости, получаем
Можно показать, что поток вектора напряжённости поля точечного заряда через замкнутую поверхность будет равен Более того, поток будет таким же, даже если поверхность будет иметь любую форму. Если поверхность охватывает несколько зарядов qi, поток каждого из зарядов через замкнутую поверхность будет равен Меняя последовательность суммирования и интегрирования и учитывая, что в соответствии с принципом суперпозиции Итак, проведённый анализ позволил получить следующее соотношение:
Это соотношение имеет универсальный характер и называется теоремой Гаусса: поток вектора напряжённости электри-ческого поля через замкнутую поверхность равен отношению суммы зарядов, охваченных этой поверхностью, к электри-ческой постоянной. Обратите внимание: в выражении теоремы Гаусса отсут-ствуют характеристики положения зарядов qi. Это означает, что поток вектора напряжённости не зависит от того, как расположены заряды, охваченные замкнутой поверх-ностью. Более того, поток вектора напряжённости не изменится, если изменится взаимное расположение зарядов, охваченных поверхностью. Практическое значение теоремы Гаусса заключается в том, что с её помощью значительно упрощается расчёт полей, созданных симметричными распределениями зарядов. В этом случае можно выбрать поверхность такой формы, что
Примеры расчёта напряжённости полей С помощью теоремы Гаусса Рассмотрим несколько примеров расчёта электростатических полей с помощью теоремы Гаусса.
Прямолинейной нити
Рассмотрим равномерно заряженную бесконечно длинную нить. Линейная плотность заряда равна t. Заряд, равномерно распределённый по нити, обладает симметрией – он симметричен относительно оси.
Поскольку расстояние от эле-ментарных зарядов до этой точки одинаково, модули напряжён-ностей Е 1 и Е 2 одинаковы. Поэтому результирующая напряжённость Е = Е 1+ Е 2 направлена перпен-дикулярно нити (см. рисунок). Очевидно, что и в других точ-ках, расположенных на таком же расстоянии от нити, напря-жённость будет иметь такую же величину и направление. Элементарные заряды и точка в поле были выбраны случайно, поэтому вывод справедлив как для всех остальных элементарных зарядов, так и для всех точек поля. Это означает, что электрическое поле, созданное заряженной нитью, симметрично относительно оси нити. Другими словами – симметрия поля тождественна симметрии заряда, создающего поле. Таким образом, векторы напряжённости во всех точках окружающего пространства перпендикулярны нити и модули напряжённости на одинаковых расстояниях от нити одинаковы.
Расчёт напряжённости поля с помощью теоремы Гаусса следует начинать с получения выражения для потока вектора Е. В свою очередь, выражение для потока следует начинать с выбора формы замкнутой поверхности и её положения относительно источника поля. Расчёт потока будет максимально прост, если выбрать такую поверхность, симметрия которой идентична симметрии создаю-щего поле заряда. В данном случае удобно пользоваться замкнутой поверхностью с осевой симметрией. Такой поверхностью является цилиндр, ось которого совпадает с нитью. Пусть высота цилиндра равна l, а радиус основания – r. Поток вектора напряжённости поля, созданного нитью, складывается из потока через торцевые поверхности цилиндра и потока через боковую поверхность. Поток через торцевые поверхности равен нулю, так как векторы напряжённости перпендикулярны нити и, соответ-ственно угол между векторами Е и n равен 900,
Поток через боковую поверхность
Поскольку все точки боковой поверхности расположены на одинаковых расстояниях от нити, модули напряжённости во всех точках боковой поверхности цилиндра одинаковы, т. е.
Таков вид выражения для потока вектора рассчитываемой напряжённости. Следующий этап вычисления напряжённости электро-статического поля – расчёт суммарного заряда, охваченного замкнутой поверхностью. Заряд, охваченный поверхностью s, можно найти так:
Тогда, по теореме Гаусса,
или
Отсюда
Таким образом, напряжённость электрического поля, создан-ного равномерно заряженной нитью, прямо пропорциональна линейной плотности заряда нити и обратно пропорциональна расстоянию от нити до интересующей нас точки. Обратите внимание – напряжённость обратно пропорцио-нальна первой степени расстояния от нити (напряжённость поля точечного заряда обратно пропорциональна квадрату расстояния от заряда). Поляризация диэлектриков
При внесении диэлектрика любого типа в электрическое поле происходит его поляризация, т. е. в нём возникает отличный от нуля дипольный электрический момент. Механизм поляризации в каждой группе диэлектриков имеет особенности. Рассмотрим его подробнее.
Начнём с рассмотрения неполярных диэлектриков.
Подобным образом ве-дут себя и диэлектрики второго типа: под действи-ем кулоновских сил поло-жительные и отрицатель-ные ионы смещаются, что приводит к возникновению дипольных моментов.
Из сказанного следует, что степень поляризации любого диэ-лектрика может быть различной. Следовательно, необходима количественная мера степени поляризации диэлектрика. В ка-честве такой меры используется поляризованность диэлектрика – дипольный момент единицы объёма диэлектрика. Это вели-чина, равная векторной сумме дипольных моментов молекул в единице объёма вещества:
Размерность вектора поляризованности
Поляризованность в диэлектриках всех типов зависит от напряжённости электрического поля. Чем больше напряжённость электрического поля, тем выше поляризованность диэлектрика. В аналитической форме эта связь имеет вид Р = keо Е, где k (каппа) – диэлектрическая восприимчивость. Диэлект-рическая восприимчивость является безразмерной величиной. Учитывая, что дипольный момент поляризованной неполяр-ной молекулы всегда направлен по полю, мы вправе утверждать, что изменение температуры не влияет на степень поляризации молекулы. Следовательно, и поляризованность, и диэлектри-ческая восприимчивость неполярного диэлектрика не зависят от температуры. Полярные диэлектрики ведут себя иначе. В них упорядо-чивающему действию внешнего электрического поля противо-действует хаотическое тепловое движение молекул, стремящееся разориентировать дипольные моменты молекул. Поэтому при каждой температуре будет устанавливаться некоторая равно-весная упорядоченность дипольных моментов. Следовательно, поляризованность и диэлектрическая восприимчивость полярных диэлектриков зависят от температуры. Чем выше температура, тем ниже поляризованность Р и диэлектрическая воспри-имчивость k. Следует отметить ещё одну важную особенность ди-электрической восприимчивости k. В изотропных средах, свойства которых не зависят от направ-ления, k является скаляром. Поэтому в изотропных диэлектриках направление вектора Р всегда параллельно направлению Е. В анизотропных диэлектриках диэлектрическая восприим-чивость, измеренная для направления, параллельного оси х, не равна значению k, измеренному для параллельного оси у на-правления. Поэтому в анизотропных диэлектриках направление вектора Р в общем случае не параллельно направлению Е. Конденсаторы
Если взять систему из двух проводников*, имеющих одинаковые по величине и противоположные по знаку заряды, то мы получим конденсатор – устройство, ёмкость которого намного больше ёмкости уединённого проводника и не зависит от ёмкости окружающих тел**. Основной характеристикой конденсатора является его ёмкость С, определяемая выражением В данном случае разность потенциалов между обкладками конденсатора равна напряжению на конденсаторе j1 – j2 = U. Поэтому определение ёмкости конденсатора можно записать в таком виде: Ёмкость конденсатора зависит от площади обкладок конденсатора, формы обкладок, расстояния между ними, ди-электрической проницаемости вещества, заполняющего прост-ранство между обкладками конденсатора. Рассмотрим в качестве примера плоский конденсатор. Это устройство из двух проводящих плоскостей, параллельных друг другу и разделённых слоем диэлектрика. Если размеры пластин достаточно велики по сравнению с расстоянием d между ними, то заряд распределён по поверхности пластин равномерно с плотностью s = q / S.
_____________________
* Такие проводники принято называть обкладками. ** Емкость конденсатора не зависит от окружающих тел, поскольку практически все поле сосредоточено между его обкладками.
Одна пластина создаёт поле напряжённостью Поскольку
Отсюда ёмкость плоского конденсатора
Соединение конденсаторов
Последовательное соединение. По-следовательным называют соединение конденсаторов, показанное на рисунке.
Внутренние обкладки конденсаторов С 1 и С 2 заряда от батареи не получают. Но если левая обкладка С 1 заряжена положительно, то на правую перетечёт такой же заряд противоположного знака с левой обкладки С 2. Поэтому все обкладки конденсаторов будут иметь одинаковые по величине заряды q. При таком соединении суммарная разность потенциалов на всех конденсаторах равна сумме разностей потенциалов на них Dj = Dj1 + Dj2. Суммарную разность потенциалов Dj можно выразить через заряд и суммарную ёмкость конденсаторов C: Разность потенциалов между обкладками каждого из конденсаторов можно выразить аналогичным образом: Заменяя разности потенциалов на приведённые выражения, получаем
и, сокращая заряд, получаем выражение для суммарной ёмкости последовательно соединённых конденсаторов
Таким образом, величина, обратная суммарной ёмкости конденсаторов, равна сумме обратных каждой из ёмкостей величин. Очевидно, что если соединены не два, а несколько конденсаторов, в сумме будет столько членов, сколько соединено конденсаторов. Параллельное соединение. Параллельным называют показанное на ри
q 1 = C 1Dj, заряд на обкладках второго – q 2 = C 2Dj. Суммарный заряд на всех конденсаторах Это означает, что С Dj = С 1Dj + С 2Dj и суммарная ёмкость конденсаторов, соединённых параллельно, равна сумме ёмкостей всех соединённых конденсаторов: С = С 1 + С 2. Энергия электрического поля
Вернёмся к выражению электрической энергии, запасённой в конденсаторе:
Для плоского конденсатора
и
В последние два выражения для расчёта энергии не входят характеристики проводников (S и d); в них энергия выражается через характеристики электрического поля. Это позволяет трактовать W как энергию электрического поля. Мы можем говорить, что это энергия электрического поля. И эта энергия распределена в пространстве с объёмной плотностью
Используя последнее выражение, можно найти энергию, запасённую в однородном электрическом поле, занимающем объём V W = w V. Если электрическое поле неоднородно, то
т. е. энергия поля в объёме V равна интегралу от объёмной плотности электрического поля, взятому по объёму V.
Электродвижущая сила
Если в проводнике создать электрическое поле, свободные заряды начнут двигаться упорядоченно, т. е. возникнет электрический ток. Однако этот ток очень быстро прекратится, так как свободные заряды перераспределятся так, что поле внутри проводника станет равно нулю и причина, вызвавшая направленное движение зарядов, исчезнет (см. разд. 1.19).
Для того чтобы ток не прекращался, необ-ходимо переносить из-быточные заряды с одного конца провод-ника на противополо-жный. Тогда электри-ческое поле внутри проводника будет су-ществовать непрерывно и направленное движение зарядов не будет прекращаться. Другими словами – для того чтобы в цепи непрерывно существовал электрический ток, в части электрической цепи свободные носители должны двигаться по электрическому полю, а в другой части – против. Естественно, электрическое поле не может заставить поло-жительные заряды двигаться против кулоновских сил. Следо-вательно, в части цепи должны действовать силы, заставляющие положительные заряды двигаться от “минуса” к “плюсу”. Такие силы неэлектростатического происхождения принято называть сторонними. Участок цепи, на котором действуют сторонние силы, называют источником ЭДС (электродвижущей силы). На практике используются различные виды источников ЭДС. Это электрические генераторы, гальванические элементы (батарейки), аккумуляторы и т. д. Источник электродвижущей силы характеризуется величиной эдс:
где А ст – работа сторонних сил по перемещению заряда q; q – заряд, перемещённый сторонними силами. Размерность ЭДС [e] = Дж/Кл = В (вольт). Работу сторонних сил по перемещению заряда q внутри источника эдс можно вычислить следующим образом:
Отсюда величина эдс
Работа по перемещению заряда на участке цепи, содержащем источник ЭДС, может быть найдена как
Учитывая связь напряжённости и потенциала, а также опреде-ление ЭДС, получаем
Величина, равная работе электростатических и сторонних сил по перемещению единичного заряда в электрической цепи, называется напряжением:
Обратите внимание: напряжение на участке цепи и разность потенциалов на его концах различны по величине. Напряжение и разность потенциалов не одно и то же! Следует отметить, что участок цепи, содержащий источник ЭДС, называют неоднородным. Участок, не содержащий источ-ника ЭДС, называют однородным. Поскольку однородный участок не содержит ЭДС, постольку
Закон Ома
Георг Ом, экспериментируя с цепями постоянного тока, обнаружил, что сила тока в участке электрической цепи определяется следующим соотношением
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 455; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.013 с.) |


 технический университет, 2005
технический университет, 2005
 ,
,
 .
.
 .
. .
.
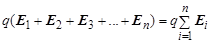 ,
, .
. , где r i – вектор, соединяющий заряд dqi c нужной точкой поля, ri – модуль вектора r i.
, где r i – вектор, соединяющий заряд dqi c нужной точкой поля, ri – модуль вектора r i.
 );
); );
); ).
). В описании таких полей часто используют понятие потока вектора через некоторую поверхность. Рас-смотрим это понятие.
В описании таких полей часто используют понятие потока вектора через некоторую поверхность. Рас-смотрим это понятие.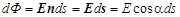 ,
,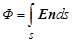 .
. ,
, Поэтому поток вектора напряжённости через элементарную поверхность ds будет равен Еn ds = E cosa ds = E cos0 ds = Eds.
Поэтому поток вектора напряжённости через элементарную поверхность ds будет равен Еn ds = E cosa ds = E cos0 ds = Eds. .
. .
. .
. .
. и в том случае, когда заряд находится не в центре сферической поверхности.
и в том случае, когда заряд находится не в центре сферической поверхности. . Суммарный поток, созданный всеми зарядами, будет равен
. Суммарный поток, созданный всеми зарядами, будет равен  .
. , получаем
, получаем  , где Е – вектор напряжённости поля, созданного всеми зарядами, охваченными замкнутой поверхностью.
, где Е – вектор напряжённости поля, созданного всеми зарядами, охваченными замкнутой поверхностью. .
. , где S ^ – площадь части замкнутой поверхности, пронизываемой электрическим полем.
, где S ^ – площадь части замкнутой поверхности, пронизываемой электрическим полем. Нить имеет бесконечную длину, поэтому любому эле-ментарному заряду dq 1 можно сопоставить другой элементарный заряд dq 2, расположенный симметрично относительно некоторой точки в электростатическом поле.
Нить имеет бесконечную длину, поэтому любому эле-ментарному заряду dq 1 можно сопоставить другой элементарный заряд dq 2, расположенный симметрично относительно некоторой точки в электростатическом поле.
 .
.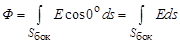 .
. .
. .
.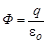
 .
. .
.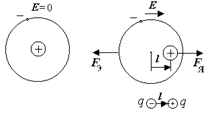 При внесении такого вещества во внешнее электрическое поле под действием кулоновских сил центры “тяжести” положи-тельных и отрицательных зарядов молекулы смеща-ются в противоположных направениях.
При внесении такого вещества во внешнее электрическое поле под действием кулоновских сил центры “тяжести” положи-тельных и отрицательных зарядов молекулы смеща-ются в противоположных направениях.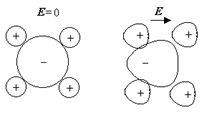 В результате центры “тяжести” положительного и отрицательного зарядов оказываются на некотором расстоянии l друг от друга (см. рисунок). Молекула неполярного диэлектрика становится диполем с плечом l, направленным параллельно вектору на-пряжённости электрического поля.
В результате центры “тяжести” положительного и отрицательного зарядов оказываются на некотором расстоянии l друг от друга (см. рисунок). Молекула неполярного диэлектрика становится диполем с плечом l, направленным параллельно вектору на-пряжённости электрического поля.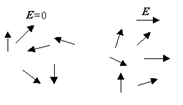 В полярных диэлектри-ках внешнее поле вызывает ориентацию молекул – молекулы ориентируются по полю. Сумма дипольных моментов молекул ста-нет отличной от нуля. Естественно, что хаотическое (тепловое) дви-жение молекул противодействует упорядочиванию ориентации мо-лекул. Поэтому при данной темпе-ратуре степень ориентации будет тем выше, чем сильнее электрическое поле.
В полярных диэлектри-ках внешнее поле вызывает ориентацию молекул – молекулы ориентируются по полю. Сумма дипольных моментов молекул ста-нет отличной от нуля. Естественно, что хаотическое (тепловое) дви-жение молекул противодействует упорядочиванию ориентации мо-лекул. Поэтому при данной темпе-ратуре степень ориентации будет тем выше, чем сильнее электрическое поле.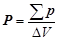 .
.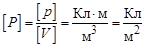 .
. , где q – заряд обкладки конденсатора, j1 – j2 – разность потенциалов между обкладками конденсатора.
, где q – заряд обкладки конденсатора, j1 – j2 – разность потенциалов между обкладками конденсатора. .
.
 ; в соответствии с принципом суперпозиции поле между пластинами
; в соответствии с принципом суперпозиции поле между пластинами 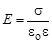 , вне пластин Е = 0.
, вне пластин Е = 0. , то
, то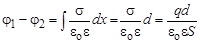 .
. .
. В практической деятельности часто используются соединения нескольких конденсаторов. Два основных способа соединения конденсаторов – параллельное и последовательное. Рассмотрим эти способы и рассчитаем суммарную ёмкость всех соединённых конденсаторов.
В практической деятельности часто используются соединения нескольких конденсаторов. Два основных способа соединения конденсаторов – параллельное и последовательное. Рассмотрим эти способы и рассчитаем суммарную ёмкость всех соединённых конденсаторов. .
. .
.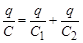
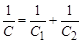 .
. сунке соединение конденсаторов.
сунке соединение конденсаторов. .
. . Поэтому его энергия
. Поэтому его энергия
 .
. .
. ,
,
 ,
, .
. .
. Если электрическая цепь замк-нута, то эдс равна
Если электрическая цепь замк-нута, то эдс равна .
. .
. .
. .
. , т. е. напряжение на однородном участке цепи равно разности потенциалов на его концах.
, т. е. напряжение на однородном участке цепи равно разности потенциалов на его концах.


