
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электроёмкость уединённого проводникаСодержание книги
Поиск на нашем сайте
Как было показано в разд. 1.14, заряженный проводник эквипотенциален, а избыточный заряд определённым образом распределён по его поверхности. Характер распределения заряда по поверхности проводника зависит от формы проводника*. Если сообщить проводнику дополнительный заряд, то он распределится по его поверхности подобно первой порции заряда, поскольку форма проводника, по условию, не изменяется. Но это означает, что при увеличении заряда уединённого проводника в n раз во столько же раз увеличится и напря-жённость поля, созданного проводником. Это, в свою очередь, означает, что в n раз возрастёт и работа, необходимая для перемещения пробного заряда из бесконечности к проводнику, т. е. его (проводника) потенциал. Следовательно, заряд проводника и его потенциал прямо пропорциональны друг другу. Отношение заряда проводника к его потенциалу называется электроёмкостью (или просто ёмкостью) уединённого провод-ника:
Размерность электроёмкости [ С ] = Кл/В = Ф (фарада). Следует заметить, что на практике используются меньшие величины единицы ёмкости. Это микрофарада (мкФ), равная Важно отметить, что ёмкость проводника зависит от окружающих его тел.
__________________
* Если вокруг данного проводника имеются другие тела, то это повлияет на распределение заряда по поверхности проводника; но в данном случае рас-сматривается уединенный проводник. Поскольку отрицательные заряды в данном случае распо-ложены к плоскости ближе, их влияние сильнее и потенциал плоскости понизится. Это означает, что ёмкость плоскости растёт. Полученный вывод является общим: электрическая ёмкость проводника, окружённого другими проводниками, всегда больше ёмкости такого же уединённого проводника.
Конденсаторы
Если взять систему из двух проводников*, имеющих одинаковые по величине и противоположные по знаку заряды, то мы получим конденсатор – устройство, ёмкость которого намного больше ёмкости уединённого проводника и не зависит от ёмкости окружающих тел**. Основной характеристикой конденсатора является его ёмкость С, определяемая выражением В данном случае разность потенциалов между обкладками конденсатора равна напряжению на конденсаторе j1 – j2 = U. Поэтому определение ёмкости конденсатора можно записать в таком виде: Ёмкость конденсатора зависит от площади обкладок конденсатора, формы обкладок, расстояния между ними, ди-электрической проницаемости вещества, заполняющего прост-ранство между обкладками конденсатора. Рассмотрим в качестве примера плоский конденсатор. Это устройство из двух проводящих плоскостей, параллельных друг другу и разделённых слоем диэлектрика. Если размеры пластин достаточно велики по сравнению с расстоянием d между ними, то заряд распределён по поверхности пластин равномерно с плотностью s = q / S.
_____________________
* Такие проводники принято называть обкладками. ** Емкость конденсатора не зависит от окружающих тел, поскольку практически все поле сосредоточено между его обкладками.
Одна пластина создаёт поле напряжённостью Поскольку
Отсюда ёмкость плоского конденсатора
Соединение конденсаторов
Последовательное соединение. По-следовательным называют соединение конденсаторов, показанное на рисунке.
Внутренние обкладки конденсаторов С 1 и С 2 заряда от батареи не получают. Но если левая обкладка С 1 заряжена положительно, то на правую перетечёт такой же заряд противоположного знака с левой обкладки С 2. Поэтому все обкладки конденсаторов будут иметь одинаковые по величине заряды q. При таком соединении суммарная разность потенциалов на всех конденсаторах равна сумме разностей потенциалов на них Dj = Dj1 + Dj2. Суммарную разность потенциалов Dj можно выразить через заряд и суммарную ёмкость конденсаторов C: Разность потенциалов между обкладками каждого из конденсаторов можно выразить аналогичным образом: Заменяя разности потенциалов на приведённые выражения, получаем
и, сокращая заряд, получаем выражение для суммарной ёмкости последовательно соединённых конденсаторов
Таким образом, величина, обратная суммарной ёмкости конденсаторов, равна сумме обратных каждой из ёмкостей величин. Очевидно, что если соединены не два, а несколько конденсаторов, в сумме будет столько членов, сколько соединено конденсаторов. Параллельное соединение. Параллельным называют показанное на ри
q 1 = C 1Dj, заряд на обкладках второго – q 2 = C 2Dj. Суммарный заряд на всех конденсаторах Это означает, что С Dj = С 1Dj + С 2Dj и суммарная ёмкость конденсаторов, соединённых параллельно, равна сумме ёмкостей всех соединённых конденсаторов: С = С 1 + С 2.
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 385; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 .
. Это объясняется тем, что окру-жающие тела значительно влияют на поле, созданное проводником, за счёт индуцированных в окружающих те-лах зарядов. Например, при прибли-жении к положительно заряженной плоскости другого проводника на нём происходит перераспределение заря-дов: на ближайшей к заряженной плоскости поверхности скапливают-ся отрицательные заряды, на удалённой – положительные. Эти заряды создают электрическое поле, которое в свою очередь влияет на распределение зарядов на плоскости.
Это объясняется тем, что окру-жающие тела значительно влияют на поле, созданное проводником, за счёт индуцированных в окружающих те-лах зарядов. Например, при прибли-жении к положительно заряженной плоскости другого проводника на нём происходит перераспределение заря-дов: на ближайшей к заряженной плоскости поверхности скапливают-ся отрицательные заряды, на удалённой – положительные. Эти заряды создают электрическое поле, которое в свою очередь влияет на распределение зарядов на плоскости. , где q – заряд обкладки конденсатора, j1 – j2 – разность потенциалов между обкладками конденсатора.
, где q – заряд обкладки конденсатора, j1 – j2 – разность потенциалов между обкладками конденсатора. .
.
 ; в соответствии с принципом суперпозиции поле между пластинами
; в соответствии с принципом суперпозиции поле между пластинами 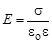 , вне пластин Е = 0.
, вне пластин Е = 0. , то
, то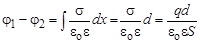 .
. .
. В практической деятельности часто используются соединения нескольких конденсаторов. Два основных способа соединения конденсаторов – параллельное и последовательное. Рассмотрим эти способы и рассчитаем суммарную ёмкость всех соединённых конденсаторов.
В практической деятельности часто используются соединения нескольких конденсаторов. Два основных способа соединения конденсаторов – параллельное и последовательное. Рассмотрим эти способы и рассчитаем суммарную ёмкость всех соединённых конденсаторов. .
. .
.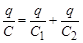
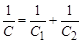 .
. сунке соединение конденсаторов.
сунке соединение конденсаторов.


