
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условия на границе раздела двух диэлектриковСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим границу раздела двух изотропных диэлектриков с диэлектрическими проницаемостями e1 и e2 (e1 < e2). Пусть на границе раздела свободные заряды отсутствуют. Оба диэлектрика находятся в однородном электрическом поле напряжённостью Е. Напряжённость электрического поля в одном из диэлектриков будет равна Е 1, во втором – Е 2.
Выберем некоторый контур, охватывающий границу раздела двух сред. Поскольку электрическое поле консервативно, работа куло-новских сил на замкнутом конту-ре A l равна нулю Al = A 12 + A 23+ A 34+ A 41=0. На участках 12 и 34 рассматриваемого контура работа
_____________________________
* В случае использования вектора напряженности теорема Гаусса имеет вид
В этих выражениях Е 1t и Е 2t – проекции векторов Е 1 и Е 2 на ось, параллельную границе раздела двух диэлектриков. Пусть l 23 = l 41 ® 0. Тогда работа кулоновских сил на этих участках будет равна нулю. Тогда работа кулоновских сил на всей длине контура Al = A 12 + A 34 = 0 и A 12 = - A 34. Последнее соотношение можно переписать в виде
Сократив одинаковые множители, получаем
Таким образом, компонента вектора напряжённости, парал-лельная границе раздела двух сред (тангенциальная компонента), с обеих сторон от границы одинакова. Вектор электрического смещения D = eoe E. Следовательно, D 1t = eoe1 E 1t, D 2t = eoe2 E 2t, А это, в свою очередь, означает, что
или
Другими словами – тангенциальная компонента вектора (D t) на границе раздела скачкообразно изменяется в соответствии с последним соотношением.
В соответствии с теоремой Гаусса, считая электрическое поле однородным, мы вправе записать*:
и
Отсюда следует, что
Таким образом, на границе раздела скачком изменяется нормальная составляющая вектора напряжённости и не изменя-ется нормальная составляющая вектора электрического смещения. Вследствие этого силовые линии на границе раздела двух диэлектриков изменяют направление**. Действительно, Е1t = Е2t, e1Е1n = e2Е2n.
Таким образом, в среде с бóль-шей диэлектрической проницаемостью (e2 >e1) силовые линии увеличивают наклон (см. рисунок)
_______________________
* Мы не будем здесь подробно описывать математические преобразования: они просты и практически одинаковы с рассмотренными перед этим. ** Если силовые линии перпендикулярны границе раздела, то их направление не изменяется.
|
|||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 422; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.145.41 (0.005 с.) |



 .
.
 .
. .
.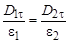
 .
. Теперь рассмотрим поведение компонент векторов D и E, перпендикулярных границе раз-дела двух диэлектриков. Для этого воспользуемся теоремой Гаусса. В качестве поверхности интегрирования выберем цилиндр бесконечно малой высоты, основания которого параллельны границе раздела двух диэлектриков.
Теперь рассмотрим поведение компонент векторов D и E, перпендикулярных границе раз-дела двух диэлектриков. Для этого воспользуемся теоремой Гаусса. В качестве поверхности интегрирования выберем цилиндр бесконечно малой высоты, основания которого параллельны границе раздела двух диэлектриков.
 .
. .
. Из рисунка видно, что
Из рисунка видно, что  . Выражая тангенс угла наклона силовых линий в каждом из диэлектриков, получим:
. Выражая тангенс угла наклона силовых линий в каждом из диэлектриков, получим: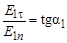 ,
,  ,
, .
.


