
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проводники в электрическом полеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Проводники – это вещества, способные проводить электрический ток. Существование проводимости в проводниках обусловлено наличием в них так называемых свободных зарядов, т. е. зарядов, способных перемещаться внутри проводника. Свободными зарядами могут быть электроны (в металлах, полупроводниках), ионы (в растворах солей, кислот и т. п.), электроны и ионы (в ионизированных газах). Все проводники во внешнем электрическом поле ведут себя практически одинаково. Рассмотрим наиболее важные особенности поведения проводников во внешнем электрическом поле. Допустим, что в рассматриваемом проводнике имеются свободные носители заряда одного знака (например, электроны). Свободные заряды в проводнике могут перемещаться, следовательно, при помещении проводника в электрическое поле они начнут двигаться в направлении действия кулоновской силы. Дошедшие до поверхности проводника заряды не могут выйти наружу. Поэтому заряды начнут скапливаться у поверхности проводника. На противоположной поверхности возникнет недостаток свободных носителей, что вызовет появление заряда противо-положного знака. Вследствие этого внутри проводника возникнет собственное электрическое поле, направленное противоположно внешнему. Пока собственное поле слабее внешнего, свободные носители будут двигаться в прежнем направлении и скапливаться на поверхности. Собственное поле при этом будет расти. Так будет до тех пор, пока собственное поле не станет равно внешнему. Суммарное поле внутри проводника при этом станет равно нулю. Полученный вывод имеет общий характер. Электрическое поле внутри любого проводника, находящегося во внешнем электрическом поле, всегда равно нулю Е = 0. Поскольку Е = -gradj = 0, постольку потенциал проводника во всех точках одинаков: j = const. В частности это означает, что поверхность проводника в электростатическом поле является эквипотенциальной. Поскольку поверхность проводника эквипотенциальна, сило-вые линии поля вне проводника перпендикулярны поверхности проводника (так как силовые линии и эквипотенциальные поверхности взаимно перпендикулярны). Если проводник зарядить, то избыточный заряд распределится по поверхности проводника. Если бы это было не так, то поле внутри проводника не могло бы быть равно нулю. Этот вывод можно получить и аналитически с помощью теоремы Гаусса: Поскольку напряжённость поля внутри проводника везде равна нулю, постольку и Избыточный заряд на проводнике находится в равновесии: заряд перераспределяется до тех пор, пока поле внутри про-водника не станет равным нулю. Как только поле внутри про-водника станет равно нулю, перераспределение, т. е. направ-ленное движение свободных зарядов, прекратится. Рассчитаем напряжённость электрического поля вблизи от поверхности заряженного проводника. Пусть поверхностная плотность заряда проводника равна s. В соответствии с теоремой Гаусса, поток вектора напря-жённости через замкнутую поверхность пропорционален заряду, охваченному этой поверхностью.
Выберем в качестве поверхности цилиндр, осно-вания которого параллельны поверхности проводника. Поток через боковую стенку цилиндра будет ра-вен нулю, так как поле вне проводника перпендикуляр-но его поверхности. Поэтому поток через по-верхность цилиндра будет равен потоку через верхнее основание площадью D S (так как внутри проводника поля нет): Е D S. Заряд, охваченный такой поверхностью, равен sD S. Тогда, в соответствии с теоремой Гаусса,
Таким образом, напряжённость поля вблизи поверхности проводника прямо пропорциональна поверхностной плотности заряда в данной точке поверхности проводника. Конечно, это не означает, что поле вне проводника не зависит от зарядов, расположенных на отдалённых точках поверхности проводника, – просто плотность зарядов в данной точке зависит от того, как распределён заряд по всей поверхности.
|
|||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 673; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 .
.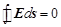 . Отсюда
. Отсюда 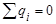 , т. е. избыточных (не скомпенсированных) зарядов внутри проводника нет.
, т. е. избыточных (не скомпенсированных) зарядов внутри проводника нет.
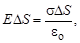
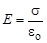 .
.


