
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поле бесконечной равномерно заряженнойСодержание книги
Поиск на нашем сайте Прямолинейной нити
Рассмотрим равномерно заряженную бесконечно длинную нить. Линейная плотность заряда равна t. Заряд, равномерно распределённый по нити, обладает симметрией – он симметричен относительно оси.
Поскольку расстояние от эле-ментарных зарядов до этой точки одинаково, модули напряжён-ностей Е 1 и Е 2 одинаковы. Поэтому результирующая напряжённость Е = Е 1+ Е 2 направлена перпен-дикулярно нити (см. рисунок). Очевидно, что и в других точ-ках, расположенных на таком же расстоянии от нити, напря-жённость будет иметь такую же величину и направление. Элементарные заряды и точка в поле были выбраны случайно, поэтому вывод справедлив как для всех остальных элементарных зарядов, так и для всех точек поля. Это означает, что электрическое поле, созданное заряженной нитью, симметрично относительно оси нити. Другими словами – симметрия поля тождественна симметрии заряда, создающего поле. Таким образом, векторы напряжённости во всех точках окружающего пространства перпендикулярны нити и модули напряжённости на одинаковых расстояниях от нити одинаковы.
Расчёт напряжённости поля с помощью теоремы Гаусса следует начинать с получения выражения для потока вектора Е. В свою очередь, выражение для потока следует начинать с выбора формы замкнутой поверхности и её положения относительно источника поля. Расчёт потока будет максимально прост, если выбрать такую поверхность, симметрия которой идентична симметрии создаю-щего поле заряда. В данном случае удобно пользоваться замкнутой поверхностью с осевой симметрией. Такой поверхностью является цилиндр, ось которого совпадает с нитью. Пусть высота цилиндра равна l, а радиус основания – r. Поток вектора напряжённости поля, созданного нитью, складывается из потока через торцевые поверхности цилиндра и потока через боковую поверхность. Поток через торцевые поверхности равен нулю, так как векторы напряжённости перпендикулярны нити и, соответ-ственно угол между векторами Е и n равен 900,
Поток через боковую поверхность
Поскольку все точки боковой поверхности расположены на одинаковых расстояниях от нити, модули напряжённости во всех точках боковой поверхности цилиндра одинаковы, т. е.
Таков вид выражения для потока вектора рассчитываемой напряжённости. Следующий этап вычисления напряжённости электро-статического поля – расчёт суммарного заряда, охваченного замкнутой поверхностью. Заряд, охваченный поверхностью s, можно найти так:
Тогда, по теореме Гаусса,
или
Отсюда
Таким образом, напряжённость электрического поля, создан-ного равномерно заряженной нитью, прямо пропорциональна линейной плотности заряда нити и обратно пропорциональна расстоянию от нити до интересующей нас точки. Обратите внимание – напряжённость обратно пропорцио-нальна первой степени расстояния от нити (напряжённость поля точечного заряда обратно пропорциональна квадрату расстояния от заряда).
|
|||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 478; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 Нить имеет бесконечную длину, поэтому любому эле-ментарному заряду dq 1 можно сопоставить другой элементарный заряд dq 2, расположенный симметрично относительно некоторой точки в электростатическом поле.
Нить имеет бесконечную длину, поэтому любому эле-ментарному заряду dq 1 можно сопоставить другой элементарный заряд dq 2, расположенный симметрично относительно некоторой точки в электростатическом поле.
 .
.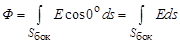 .
. .
. .
.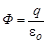
 .
. .
.


