
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электрическое поле. НапряжённостьСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Электрического поля
В соответствии с законом Кулона, электрические заряды действуют друг на друга при любом расстоянии между ними. Это объясняется тем, что каждый заряд создаёт вокруг себя электрическое поле. Любой другой заряд, помещённый в электрическое поле, взаимодействует с ним, вследствие чего на заряд действует кулоновская сила. Величина кулоновской силы, действующей на заряд, зависит от электрического поля. Чем сильнее поле, тем больше сила. Но как количественно охарактеризовать электрическое поле? Ввести такую характеристику можно следующим образом. Пусть в некоторую точку электрического поля мы поочерёдно помещаем разные заряды и измеряем силу, действующую на них:
Здесь F 1 – сила, действовавшая на заряд q 1, помещённый в интересующую нас точку поля, F 2 – сила, действовавшая на заряд q 2, и т. д. Поскольку заряды разные, то и силы будут различны по величине. Но оказывается, что отношение силы, действующей на данный заряд, к его величине не зависит от величины этого заряда
____________________________
* Размерность электрической постоянной часто записывают в ином виде: Кл2/(Н×м2) = Ф/м; здесь Ф – размерность электрической емкости (читается – «фарада»).
Величина Е, равная отношению силы, действующей на заряд, помещённый в заданную точку электрического поля (пробный заряд), к величине этого заряда называется напряжённостью
Можно также сказать, что напряжённость численно равна силе, действующей на единичный положительный пробный заряд. Напряжённость является векторной величиной. Направление вектора напряжённости совпадает с направлением силы, действующей на положительный пробный заряд. Если в качестве пробного используется отрицательный заряд, то вектор напряжённости будет противоположен направлению силы, действующей на отрицательный пробный заряд. Размерность напряжённости, как это видно из определения, [E] = Н/Кл = В/м*. Напряжённость является силовой характеристикой элект-рического поля**, поскольку определяет силу, действующую на заряд, помещённый в данную точку электрического поля. Следует обратить внимание на одну важную деталь. Пробный заряд должен быть малым по величине. Но можно ли считать малым заряд, например в 0,1 Кл? Или 0,01 Кл? Критерием малости пробного заряда является влияние этого заряда на заряды, создающие исследуемое электрическое поле. Пробный заряд мал, если его появление в электрическом поле не вызывает изменения положения зарядов, создающих элект-рическое поле. Найдём напряжённость поля, созданного точечным зарядом q. Для этого на расстоянии r от заряда q поместим пробный заряд q о. Тогда сила, действующая на пробный заряд, в соответствии с законом Кулона равна
_________________________
* Размерность В/м будет получена позже. ** В этом заключается физический смысл напряженности.
Отсюда напряжённость поля точечного заряда q равна
Таким образом, напряжённость поля, созданного точечным зарядом q в интересующей нас точке, прямо пропорциональна величине заряда, создающего поле, и обратно пропорциональна квадрату расстояния от заряда до интересующей нас точки. Полученное выражение позволяет рассчитать напряжённость электрического поля, созданного точечным зарядом, в любой его точке. Зная напряжённость электрического поля в нужной точке, легко рассчитать силу, которая будет действовать на заряд, помещённый в эту точку F = q E, где Е – напряжённость электрического поля в точке распо-ложения заряда q.
Принцип суперпозиции
Закон Кулона описывает взаимодействие двух точечных зарядов. Однако взаимодействовать одновременно могут и три, и более зарядов. Как описать взаимодействие в этом случае? Экспериментально доказано, что взаимодействие двух точечных зарядов не зависит от наличия третьего заряда. Отсюда следует, что если необходимо найти силу F, действующую на заряд q со стороны зарядов q 1, q 2, q 3... qn, достаточно рассчитать силу F 1, действующую на заряд q со стороны заряда q 1, F 2 – со стороны заряда q 2, и т. д., а затем найти их равнодействующую F = F 1 + F2 + F 3 +...+ Fn Другими словами – результат взаимодействия заряда с несколькими другими зарядами является результатом наложения (суперпозиции) взаимодействий заряда q с каждым из зарядов Поэтому сила, действующая на заряд со стороны нескольких других зарядов, равна векторной сумме всех сил, действующих на интересующий нас заряд со стороны каждого из окружающих его зарядов в отдельности. Это выражение представляет собой одну из возможных формулировок принципа суперпозиции. Выражение для расчёта силы F можно записать в следующем виде:
= где Е 1 – напряжённость поля, созданного зарядом q 1 в точке расположения заряда q, Е 2 – напряжённость поля, созданного там же вторым зарядом, Е i – напряжённость поля, созданного i – м зарядом в точке расположения заряда q. Сокращая q, получаем
Таким образом, напряжённость поля, созданного не-сколькими зарядами в интересующей нас точке, равна век-торной сумме напряжённостей, созданных каждым из заря-дов в этой точке. Данное выражение представляет собой принцип супер-позиции для вектора напряжённости электрического поля. В ряде случаев поле создаётся не точечными, а так называемыми распределёнными зарядами. Например, поле, соз-данное заряженной нитью. В таких ситуациях распределённый заряд делят на малые порции dqi, после чего рассчитывают напряжённость поля, используя принцип суперпозиции: Учитывая, что dqi является малой величиной, суммирование целесообразно заменить интегрированием
Величина dq может быть выражена следующим образом: – если заряд распределён по линии, то dq = t dl, где t – линейная плотность заряда (это заряд единицы длины заряженной нити: – если заряд распределён по поверхности, то dq = s ds, где s – поверхностная плотность заряда (это заряд единицы площади заряженной поверхности: – если заряд распределён по объёму, то dq = r dV, где r – объёмная плотность заряда (это заряд единицы объёма заряженного тела: Важно отметить, что принцип суперпозиции полей справедлив для сред, свойства которых не зависят от величины напряжённости электрического поля. Например, в вакууме поле, созданное несколькими зарядами, равно сумме полей, созданных каждым из зарядов в отдельности. Для сегнетоэлектриков это утверждение неверно, так как их электрические свойства очень сильно зависят от напряжённости поля в сегнетоэлектрике. Для большинства сред (газы, аморфные вещества, ряд кристаллических веществ) в слабых электрических полях прин-цип суперпозиции справедлив.
Поток вектора напряжённости
В ряде разделов курса общей физики рассматриваются векторные поля (например, электростатическое поле, магнитное поле).
Пусть в некоторой области пространства существует электрическое поле. Выберем в этом поле элементарную площадку ds. Пусть нормаль к этой площадке n образует угол a c вектором напряжённости электрического поля (модуль вектора n = 1). Потоком вектора напряжённости электрического поля через эту площадку называется величина, равная
где dФ – элементарный поток вектора напряжённости, Е – вектор напряжённости поля в пределах бесконечно малой площадки площадью d s. Произведение En является скалярным, поэтому поток вектора напряжённости является скалярной величиной. Иногда произведение n ds заменяют на вектор d s, который направлен перпендикулярно плоскости площадки; модуль вектора ds равен площади элементарной площадки. Поток напряжённости через конечную площадь s равен
В зависимости от величины угла между нормалью к площадке и вектором Е поток может быть положительным и отрицательным. Если угол между векторами Е и n острый, то поток положителен, если тупой – отрицателен. Обратите внимание на то, что направление вектора n выбирается перед решением задачи произвольно (перпендикуляр к поверхности можно направить в две взаимно противоположные стороны). Поэтому знак потока вектора напряжённости опреде-ляется выбором направления вектора n. Если поверхность замкнутая, поток вектора напряжённости равен
т. е. интеграл берётся по замкнутой поверхности s. В этом случае принято направлять вектор n наружу от поверхности. При этом поток через замкнутую поверхность положителен, если суммарный заряд, охваченный замкнутой поверхностью, положителен. Размерность потока вектора напряжённости [Ф]=В.м=Н.м2/Кл.
Теорема Гаусса
Теорема Гаусса – основная теорема электростатики. Она устанавливает связь между потоком вектора напряжённости через замкнутую поверхность и суммарным зарядом, охваченным этой поверхностью. Рассмотрим эту теорему. Пусть электрическое поле создано положительным точечным зарядом q. Найдём поток вектора напряжённости электрического поля через замкнутую поверхность, охватывающую этот заряд. В качестве поверхности выберем сферу радиуса r, центр которой совпадает с зарядом q. Будем считать, что векторы n во всех точках замкнутой поверхности направлены от центра сферы. Поскольку заряд, создающий поле, положителен и распо-ложен в центре сферы, постольку угол между вектором Е и вектором n во всех точках поверхности равен нулю.
Другими словами, в рассматриваемой ситуации скалярное произведение вектора напряжённости электростатического поля на вектор элементарной поверхности ра-вен произведению модулей этих век-торов. Напряжённость поля, созданного то-чечным зарядом, равна Поскольку заряд расположен в центре сферической по-верхности, расстояние от заряда до поверхности во всех её точках одинаково и равно r. Следовательно, модуль вектора напряжённости во всех точках сферической поверхности одинаков: E = const. Константу можно вынести за знак интеграла, поэтому поток вектора напряжённости через замкнутую поверхность в данном случае равен Интеграл от элементарных площадей поверхности s, взятый по всей поверхности, равен площади этой поверхности s. Таким образом, поток вектора напряжённости через замкнутую поверхность в данном случае равен Подставив выражение для расчёта напряжённости, получаем
Можно показать, что поток вектора напряжённости поля точечного заряда через замкнутую поверхность будет равен Более того, поток будет таким же, даже если поверхность будет иметь любую форму. Если поверхность охватывает несколько зарядов qi, поток каждого из зарядов через замкнутую поверхность будет равен Меняя последовательность суммирования и интегрирования и учитывая, что в соответствии с принципом суперпозиции Итак, проведённый анализ позволил получить следующее соотношение:
Это соотношение имеет универсальный характер и называется теоремой Гаусса: поток вектора напряжённости электри-ческого поля через замкнутую поверхность равен отношению суммы зарядов, охваченных этой поверхностью, к электри-ческой постоянной. Обратите внимание: в выражении теоремы Гаусса отсут-ствуют характеристики положения зарядов qi. Это означает, что поток вектора напряжённости не зависит от того, как расположены заряды, охваченные замкнутой поверх-ностью. Более того, поток вектора напряжённости не изменится, если изменится взаимное расположение зарядов, охваченных поверхностью. Практическое значение теоремы Гаусса заключается в том, что с её помощью значительно упрощается расчёт полей, созданных симметричными распределениями зарядов. В этом случае можно выбрать поверхность такой формы, что
Примеры расчёта напряжённости полей С помощью теоремы Гаусса Рассмотрим несколько примеров расчёта электростатических полей с помощью теоремы Гаусса.
|
||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 609; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |


 .
.
 .
. .
.
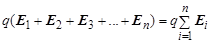 ,
, .
. , где r i – вектор, соединяющий заряд dqi c нужной точкой поля, ri – модуль вектора r i.
, где r i – вектор, соединяющий заряд dqi c нужной точкой поля, ri – модуль вектора r i.
 );
); );
); ).
). В описании таких полей часто используют понятие потока вектора через некоторую поверхность. Рас-смотрим это понятие.
В описании таких полей часто используют понятие потока вектора через некоторую поверхность. Рас-смотрим это понятие.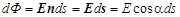 ,
,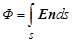 .
. ,
, Поэтому поток вектора напряжённости через элементарную поверхность ds будет равен Еn ds = E cosa ds = E cos0 ds = Eds.
Поэтому поток вектора напряжённости через элементарную поверхность ds будет равен Еn ds = E cosa ds = E cos0 ds = Eds. .
. .
. .
. .
. и в том случае, когда заряд находится не в центре сферической поверхности.
и в том случае, когда заряд находится не в центре сферической поверхности. . Суммарный поток, созданный всеми зарядами, будет равен
. Суммарный поток, созданный всеми зарядами, будет равен  .
. , получаем
, получаем  , где Е – вектор напряжённости поля, созданного всеми зарядами, охваченными замкнутой поверхностью.
, где Е – вектор напряжённости поля, созданного всеми зарядами, охваченными замкнутой поверхностью. .
. , где S ^ – площадь части замкнутой поверхности, пронизываемой электрическим полем.
, где S ^ – площадь части замкнутой поверхности, пронизываемой электрическим полем.


