
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь напряжённости и потенциала электростатического поляСодержание книги
Поиск на нашем сайте Работа электростатического поля по перемещению пробного заряда из точки 1 в точку 2
Интегрирование проводится по произвольной кривой, соединяющей точки 1 и 2. Интегральная связь напряжённости и потенциала электростатического поля
Элементарная работа поля
Градие́нт -вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины Потенциал – непрерывная функция координат! График потенциала никогда не имеет разрывов. Методы расчёта потенциала электростатического поля: метод суперпозиий и интегральная связь Е и φ.
По тонкому кольцу равномерно распределён заряд Q > 0. Пусть потенциал равен нулю в бесконечно удалённой точке. Разобьём кольцо на малые участки с зарядами dq и воспользуемся методом суперпозиций: Этот же результат можно получить методом суперпозиции (билет №2) Потенциал электростатического поля. Связь между напряженностью поля и потенциалом (интегральная и дифференциальная). Примеры расчета потенциала электростатического поля. Диполь в электростатическом поле.
Потенциалом электростатического поля [ φ ] = В (вольт) называется физическая величина, равная отношению потенциальной энергии заряда q0 в данной точке пространства, к величине этого заряда.
Связь напряжённости и потенциала электростатического поля Работа электростатического поля по перемещению пробного заряда из точки 1 в точку 2
Интегрирование проводится по произвольной кривой, соединяющей точки 1 и 2. Интегральная связь напряжённости и потенциала электростатического поля
Элементарная работа поля 6. 7. Методы расчёта потенциала электростатического поля: метод суперпозиий и интегральная связь Е и φ. Пример расчета напряженности Электрического поля равномерно заряженного тонкого кольца
1. По принципу суперпозиции полей: – где dE - напряжённость электрического поля малого заряда dq. Векторы напряжённости электрического поля каждого из этих зарядов одинаковы по модулю и направлены так, что концы этих векторов образуют конус с вершиной в точке A (штриховой линией показано основание этого конуса). Проекции этих векторов на плоскость кольца компенсируются, поэтому суммарный вектор направлен вдоль оси z: E (при z > 0). Вычислим Ez. Напряжённость поля точечного заряда:
2. Найдём напряжённость электрического поля как функцию z через дифференциальную связь напряжённости и потенциала:
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 428; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |

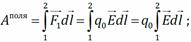 разность потенциалов при этом :
разность потенциалов при этом : 

 – потенциал поля в точке 1.
– потенциал поля в точке 1. элементарное приращение потенциала
элементарное приращение потенциала 
 – дифференциальная связь напряжённости и потенциала электростатического поля.
– дифференциальная связь напряжённости и потенциала электростатического поля. , значение которой меняется от одной точки пространства к другой, а по величине (модулю) равный быстроте роста этой величины в этом направлении.
, значение которой меняется от одной точки пространства к другой, а по величине (модулю) равный быстроте роста этой величины в этом направлении.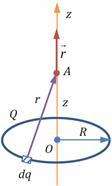 Пример: Поле равномерно заряженного тонкого кольца
Пример: Поле равномерно заряженного тонкого кольца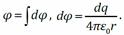 Расстояние r до точки A, где измеряется потенциал, одинаково для всех элементов dq:
Расстояние r до точки A, где измеряется потенциал, одинаково для всех элементов dq:  . Проинтегрируем выражение для потенциала по q:
. Проинтегрируем выражение для потенциала по q:  Найдём напряжённость электрического поля как функцию z через дифференциальную связь напряжённости и потенциала:
Найдём напряжённость электрического поля как функцию z через дифференциальную связь напряжённости и потенциала:  .
. 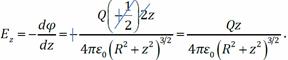
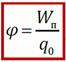
 Разность потенциалов – это работа поля по перемещению пробного заряда из начального положения в конечное, отнесённая к модулю этого заряда и взятая с обратным знаком, или работа внешних сил при том же перемещении, отнесённая к модулю пробного заряда.
Разность потенциалов – это работа поля по перемещению пробного заряда из начального положения в конечное, отнесённая к модулю этого заряда и взятая с обратным знаком, или работа внешних сил при том же перемещении, отнесённая к модулю пробного заряда. разность потенциалов при этом :
разность потенциалов при этом : 

 – потенциал поля в точке 1.
– потенциал поля в точке 1. элементарное приращение потенциала
элементарное приращение потенциала 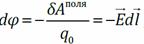
 – дифференциальная связь напряжённости и потенциала электростатического поля.
– дифференциальная связь напряжённости и потенциала электростатического поля.
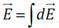 По тонкому кольцу равномерно распределён заряд Q > 0. Находим напряжённость электрического поля в точке A на оси кольца (OA = z). Разобьём кольцо на точечные заряды dq (на рисунке показаны два малых заряда dq и dq′, равные по модулю и расположенные диаметрально противоположно).
По тонкому кольцу равномерно распределён заряд Q > 0. Находим напряжённость электрического поля в точке A на оси кольца (OA = z). Разобьём кольцо на точечные заряды dq (на рисунке показаны два малых заряда dq и dq′, равные по модулю и расположенные диаметрально противоположно).
 Величины r и θ (угол) одинаковы для всех элементов dq:
Величины r и θ (угол) одинаковы для всех элементов dq:
 подставим
подставим  В этом выражении все величины – постоянные, кроме dq. Проинтегрируем по q:
В этом выражении все величины – постоянные, кроме dq. Проинтегрируем по q: 
 .
. 
 Электрический диполь – система двух точечных зарядов, одинаковых по модулю и противоположных по знаку.
Электрический диполь – система двух точечных зарядов, одинаковых по модулю и противоположных по знаку.


