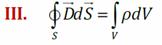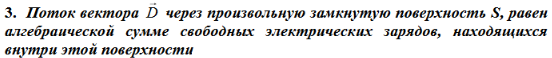Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диполь. Расчет поля диполя в дальней зоне. Диполь в электростатическом поле. Вращающий момент силы. Энергия диполя в электростатическом поле.Содержание книги
Поиск на нашем сайте
которого l = const. Рассмотрим точечный диполь, т. е. диполь на расстояниях r >> l.
потенциал [при φ (∞) = 0], α – угол между
модуль напряжённости электрического поля Диполь в электростатическом поле
Пусть в пространстве имеется однородное электрическое поле, напряжённость поля. Диполь расположен под углом α к силовым линиям поля. Сила, с которой поле действует на диполь
В этом случае При этом возникает вращающий момент М, создаваемый парой сил. Когда диполь оказывается ориентирован вдоль Е (вектора напряженности), это векторное произведение равно нулю, и вращающего момента не возникает.
Рассмотрим диполь в однородном электрическом поле. Потенциальная энергия диполя:
График зависимости потенциальной энергии диполя от угла между дипольным моментом и напряжённостью электрического поля представлен на рисунке. Диполь находится в положении равновесия при F=0, т. е. в точках экстремума потенциальной энергии: α = 0 – устойчивое равновесие; α = π – неустойчивое равновесие. Электрическое поле в веществе. Диэлектрики. Типы диэлектриков. Электронная и ориентационная поляризации. Вектор поляризации и его связь с поверхностными и объемными связанными зарядами. Теорема Остроградского-Гаусса для вектора Р. Проводники – вещества, имеющие свободные заряды – заряженные частицы, свободно перемещающиеся по образцу. Диэлектрики – вещества, в которых заряженные частицы связаны в пределах молекул и могут перемещаться под действием внешнего поля только на расстояния не более межмолекулярных.Любой диэлектрик можно превратить в проводник, т. е. пробить. Типы поляризации диэлектрика
В отсутствие электрического поля
При наличии электрического поля
Электрическое поле в диэлектрике складывается из двух полей – поля свободных зарядов (внешнего электрического поля) и поля связанных зарядов:
Дипольный момент молекулы параллелен и пропорционален напряжённости электрического поля:
В поляризованном диэлектрике на его краях образуются связанные заряды. Каждый из связанных зарядов входит в состав диполя. σ св — поверхностная плотность связанных зарядов. Установим связь между поверхностной плотностью связанных зарядов (σ св) и вектором поляризации(⃗ P). Вид сбоку на пластину диэлектрика. ⃗ E ⊥ пластине
Поверхностная плотность связанных зарядов равна проекции вектора поляризации на внешнюю нормаль (Pn) к поверхности диэлектрика. Теорема Остроградского-Гаусса для вектора Р: поток поляризованности сквозь произвольную замкнутую поверхность равен сумме связанных зарядов, охваченной этой поверхностью, взятой с обратным знаком.
Сторонние и связанные заряды диэлектрика. Вывод теоремы Остроградского-Гаусса для поля в диэлектрике. Вектор электрического смещения н его связь с напряженностью поля. Диэлектрическая проницаемость вещества. Третье уравнение Максвелла. Сторонние заряды – это заряды, расположенные за пределами диэлектрика, а также заряды, которые хотя и находятся в пределах диэлектрика, но не входят в состав его молекул. Связанные заряды – это заряды, входящие в состав атомов и молекул диэлектрика. Под действием поля они могут лишь немного смещаться из своих положений равновесия. Плотность связанных зарядов равна по абсолютной величине проекции поляризованности на направление внешней нормали рассматриваемой поверхности
– электрическое смещение (электрическая индукция);
- теорема Остроградского-Гаусса для электрического смещения: поток вектора электрического смещения сквозь произвольную замкнутую поверхность равен сумме свободных зарядов, охваченных этой поверхностью.
Где ε- Относительнаядиэлектри́ческаяпроница́емость среды. Относительнаядиэлектри́ческаяпроница́емость среды — физическая величина, характеризующая свойства изолирующей (диэлектрической) среды и показывающая, во сколько раз сила взаимодействия двух электрических зарядов в этой среде меньше, чем в вакууме. Значение ε вакуума равно единице, для реальных сред ε > 1. Для воздуха и большинства других газов в нормальных условиях значение ε близко к единице в силу их низкой плотности. Электрическая постояннаяε0 ≈ 8.85·10−12 Ф/м Третье уравнение Максвелла определяет источники электрического поля. Физический смысл этого уравнения состоит в том, что электрическое поле в некоторой области пространства связано с электрическим зарядом внутри этой поверхности.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 552; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.134.165 (0.009 с.) |

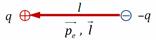 Электрический диполь – система двух точечных зарядов, одинаковых по модулю и противоположных по знаку. Заряд диполя q – модуль заряда каждой из частиц (полюсов) диполя. Плечо диполя l – расстояние между полюсами.
Электрический диполь – система двух точечных зарядов, одинаковых по модулю и противоположных по знаку. Заряд диполя q – модуль заряда каждой из частиц (полюсов) диполя. Плечо диполя l – расстояние между полюсами.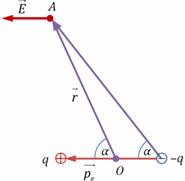 Дипольный момент – векторная характеристика:
Дипольный момент – векторная характеристика: 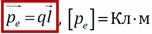 . Вектор дипольного момента направлен от отрицательного полюса к положительному. Будем рассматривать жёсткий диполь, т. е. для
. Вектор дипольного момента направлен от отрицательного полюса к положительному. Будем рассматривать жёсткий диполь, т. е. для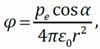 Методом суперпозиций можно получить следующие результаты:
Методом суперпозиций можно получить следующие результаты: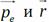 – показан на рисунке
– показан на рисунке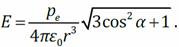
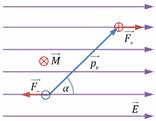 а) Однородное поле - диполь разворачивается вдоль силовых линий.
а) Однородное поле - диполь разворачивается вдоль силовых линий. 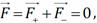 так как
так как 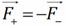 . Но момент пары сил
. Но момент пары сил  . Выразим этот момент относительно любой оси, перпендикулярной плоскости рисунка, например, оси z, проходящей через отрицательный полюс диполя:
. Выразим этот момент относительно любой оси, перпендикулярной плоскости рисунка, например, оси z, проходящей через отрицательный полюс диполя: 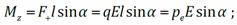
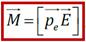
 б) Неоднородное поле
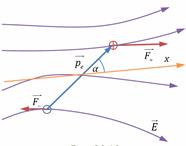
б) Неоднородное поле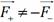 , диполь не только разворачивается вдоль силовых линий, но и втягивается в область более сильного поля. Равнодействующая
, диполь не только разворачивается вдоль силовых линий, но и втягивается в область более сильного поля. Равнодействующая 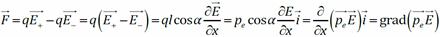
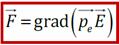
 Энергия диполя в электрическом поле
Энергия диполя в электрическом поле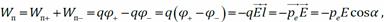
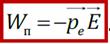 Так как
Так как  , из этого выражения получается, что
, из этого выражения получается, что 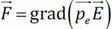 -
-


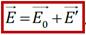
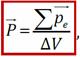 Вектор поляризации (Поляризованность) P – векторная характеристика поляризации вещества, равная сумме дипольных моментов молекул вещества, занимающего единичный объём.
Вектор поляризации (Поляризованность) P – векторная характеристика поляризации вещества, равная сумме дипольных моментов молекул вещества, занимающего единичный объём.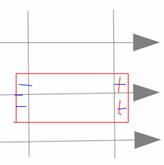
 где β – поляризуемость молекулы.
где β – поляризуемость молекулы.  здесь N – число молекул, n – концентрация. Обозначим
здесь N – число молекул, n – концентрация. Обозначим 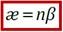 – диэлектрическая восприимчивость вещества;
– диэлектрическая восприимчивость вещества; 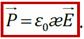
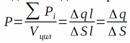 В общем случае σ св = Pn
В общем случае σ св = Pn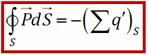
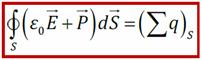 Теорема Остроградского-Гаусса утверждает: п оток вектора напряженности электростатического поля
Теорема Остроградского-Гаусса утверждает: п оток вектора напряженности электростатического поля 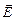 через произвольную замкнутую поверхность
через произвольную замкнутую поверхность 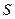 прямо пропорционален алгебраической сумме свободных зарядов, расположенных внутри этой поверхности.
прямо пропорционален алгебраической сумме свободных зарядов, расположенных внутри этой поверхности.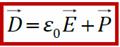
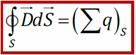
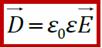 D – это вспомогательная векторная характеристика электрического поля, помогающая расчёту E. Связь напряженности (Е) и вектора электрического смещения (D)
D – это вспомогательная векторная характеристика электрического поля, помогающая расчёту E. Связь напряженности (Е) и вектора электрического смещения (D)