
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Явление самоиндукции и взаимной индукции. Индуктивность. Взаимная Индуктивность, расчет индуктивности тонкого тороида и длинного соленоида. Трансформатор.Содержание книги
Поиск на нашем сайте
Рассмотрим замкнутый проводник (проводящий контур), по которому идёт ток, создающий магнитное поле – собственное магнитное поле проводника. Если этот ток – переменный, то магнитный поток сквозь поверхность, натянутую на контур с током (собственный магнитный поток), будет изменяться и возникнет индуцированное электрическое поле. Самоиндукция – частный случай явления электромагнитной индукции – возникновение электрического поля в замкнутой цепи в результате изменения силы тока в этой цепи. Собственный магнитный поток
Закон Фарадея-Максвелла в случае самоиндукции запишется как: E s – ЭДС самоиндукции.
[L] = Гн (генри).
Пусть имеются два замкнутых проводящих контура 1 и 2, расположенные достаточно близко друг к другу (РИС. 26.9). По контуру 1 идёт ток I 1, так что контур 2 находится в магнитном поле контура 1. Поток индукции магнитного поля контура 1 сквозь поверхность, натяну- тую на контур 2, Φ12 ~ I 1, так как B 1 ~ I 1. Если ток I 1 переменный, то в проводнике 2 возникает переменное электрическое поле и ток I 2. В свою очередь, контур 2 создаёт магнитное поле, пронизывающее контур 1; соответственно, магнитный поток Φ21 ~ I 2. Таким образом два проводника влияют друг на друга. Взаимная индукция – частный случай явления электромагнитной индукции – возникновение электрического поля в проводнике под действием переменного тока в другом проводнике, близко расположенным к данному проводнику. Магнитный поток сквозь поверхность, натянутую на проводник 2, создаваемый проводником 1,
Закон Фарадея-Максвелла для случая взаимной индукции: Трансформа́тор — это статическое электромагнитное устройство, имеющее две или более индуктивно связанные обмотки на каком-либо магнитопроводе и предназначенное для преобразования посредством электромагнитной индукции одной или нескольких систем (напряжений) переменного тока в одну или несколько других систем (напряжений), без изменения частоты. Трансформатор осуществляет преобразование переменного напряжения и/или гальваническую развязку в самых различных областях применения — электроэнергетике, электронике и радиотехнике. Конструктивно трансформатор может состоять из одной (автотрансформатор) или нескольких изолированных проволочных, либо ленточных обмоток (катушек), охватываемых общим магнитным потоком, намотанных, как правило, на магнитопровод (сердечник) из ферромагнитногомагнитомягкого материала. 21. Энергия магнитного поля контура с током (вывод). Объемная плотность энергии магнитного поля. Пример расчета энергии магнитного поля.
Рассмотрим контур индуктивностью L, по которому протекает ток I. С этим контуром сцеплен магнитный поток Ф=LI, поскольку индуктивность контура неизменна, то при изменении тока на dI магнитный поток изменяется на dФ=LdI. Но для изменения магнитного потока на величину dФ следует совершить работу dА=IdФ=LIdI. Тогда работа по созданию магнитного потока Ф равна:
Значит, энергия магнитного поля, которое связано с контуром: Энергию магнитного поля можно рассматривать как функцию величин, которые характеризуют это поле в окружающем пространстве. Для этого рассмотрим частный случай — однородное магнитное поле внутри длинного соленоида. Подставив в формулу (1) формулу индуктивности соленоида, найдем
Магнитное поле внутри соленоида однородно и сосредоточено внутри него, поэтому энергия (2) заключена в объеме соленоида и имеет с нем однородное распределение с постоянной объемной плотностью
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 247; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.60.193 (0.009 с.) |

 где – B s - индукция собственного магнитного поля проводника. Так как Bs ~ I (току в проводнике), Φ s ~ I.
где – B s - индукция собственного магнитного поля проводника. Так как Bs ~ I (току в проводнике), Φ s ~ I. Потокосцепление – суммарный собственный магнитный поток проводника, име-ющего более одного витка:
Потокосцепление – суммарный собственный магнитный поток проводника, име-ющего более одного витка:
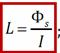 Индуктивность – характеристика проводника, равная отношению собственного магнитного потока (потокосцепления) к току в проводнике:
Индуктивность – характеристика проводника, равная отношению собственного магнитного потока (потокосцепления) к току в проводнике: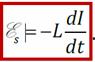 Индуктивность зависит от формы и размеров проводника (а также магнитных свойств среды) и не зависит от силы тока, магнитной индукции и других характеристик поля и тока. Из определения индуктивности следует, что Φs= LI. Подставим это выражение в закон Фарадея-Максвелла
Индуктивность зависит от формы и размеров проводника (а также магнитных свойств среды) и не зависит от силы тока, магнитной индукции и других характеристик поля и тока. Из определения индуктивности следует, что Φs= LI. Подставим это выражение в закон Фарадея-Максвелла


 – коэффициент взаимной индукции (взаимная индуктивность) – характеристика взаимного влияния проводников. Коэффициент взаимной индукции зависит от формы, размера проводников, их взаимного расположения, магнитных свойств среды. Возможно M12 < 0. в отсутствие ферромагнетиков коэффициенты взаимной индукции равны:
– коэффициент взаимной индукции (взаимная индуктивность) – характеристика взаимного влияния проводников. Коэффициент взаимной индукции зависит от формы, размера проводников, их взаимного расположения, магнитных свойств среды. Возможно M12 < 0. в отсутствие ферромагнетиков коэффициенты взаимной индукции равны: – это теорема взаимности.
– это теорема взаимности.

 (1)
(1) . Так как I=B l /(μ0μN) и В=μ0μH, то
. Так как I=B l /(μ0μN) и В=μ0μH, то  (2)
(2)  (3)
(3) 


