
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения Максвелла в интегральной формеСодержание книги
Поиск на нашем сайте
Физический смысл:магнитное поле создаётся не только токамиповодимости, но и изменяющимся во времени электрическим полем.
Физический смысл:оно показывает, что источником электростатического поля являются свободные электрические заряды.
Физический смысл:оно показывает, что в природе не существует магнитных зарядов.
I – сила тока, dS – элементарная площадка, перпендикулярная направлению движения зарядов, t – время Имеются в виду свободные заряды – заряды, нарушающие электронейтральность вещества, и макротоки – упорядоченное движение заряженных частиц, при котором они перемещаются на расстояния, много большие межмолекулярных расстояний. В уравнениях I, II L – произвольная замкнутая кривая, S – произвольная поверхность, ограниченная этой кривой. В уравнениях III, IV S – произвольная замкнутая поверхность, V – объём, ограниченный этой поверхностью. Это фундаментальные уравнения теории электромагнитного поля. Из анализа 1-го и 2-го законов Максвелла следует, что переменное магнитное поле порождает вихревое электрическое, а переменное электрическое поле порождает магнитное, то есть переменные электрическое и магнитное поля неразрывно связаны друг с другом и являются просто проявлениями единого электромагнитного поля. Электростатическое поле. Вектор напряженности поля и методы его расчета. Принцип суперпозиции полей. Примеры расчета напряженности поля методом суперпозиции (кольцо). Электростатическое поле — поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами (при отсутствии электрических токов). Электрическое поле представляет собой особый вид материи, связанный с электрическими зарядами и передающий действия зарядов друг на друга. Если в пространстве имеется система заряженных тел, то в каждой точке этого пространства существует силовое электрическое поле. Оно определяется через силу, действующую на пробный точечный заряд, помещённый в это поле. Пробный заряд должен быть ничтожно малым, чтобы не повлиять на характеристику электростатического поля.Электрическое поле называют однородным, если вектор его напряженности одинаков во всех точках поля. Основные характеристики электростатического поля:напряженность и потенциал
Принцип суперпозиции полей гласит, что напряжённость электрического поля, создаваемого системой заряженных частиц, равна сумме напряжённостей полей, создаваемых каждым из этих зарядов в отдельности. Любую систему заряженных тел можно разбить на точечные заряды (или заряды другой формы, поле которых легко рассчитать) и затем просуммировать (проинтегрировать) напряжённости полей этих зарядов.
Пример расчета напряженности Электрического поля равномерно заряженного тонкого кольца
Векторы напряжённости электрического поля каждого из этих зарядов одинаковы по модулю и направлены так, что концы этих векторов образуют конус с вершиной в точке A (штриховой линией показано основание этого конуса). Проекции этих векторов на плоскость кольца компенсируются, поэтому суммарный вектор направлен вдоль оси z: E (при z > 0). Вычислим Ez. Напряжённость поля точечного заряда:
В этом выражении все величины – постоянные, кроме dq. Проинтегрируем по q:
Поток вектора напряженности. Теорема Остроградского-Гауса для электростатического поля в вакууме. Применение теоремы к расчету напряженности поля. Пример: поле бесконечно большой равномерно заряженной плоскости.
Элементарный поток направлен по внешней нормали к малому участку dS (Если поверхность S не замкнута, то выбор одного из двух направлений нормали произволен, при этом направление нормали для всех участков dS должно быть одинаковым)
Полный поток вектора сквозь поверхность S E
Теорема Остроградского-Гаусса для: поток вектора напряжённости электрического поля сквозь произвольную замкнутую поверхность равен алгебраической сумме зарядов, охваченной этой поверхностью, делённой на ε 0:
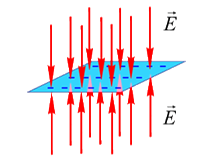
Поле равномерно заряженной бесконечной плоскости: Работа сил электростатического поля по перемещению заряда. Потенциал электростатического поля. Связь между напряженностью поля и потенциалом. Понятие градиента. Методы расчета потенциала. Пример: потенциал на оси равномерно заряженного кольца. I уравнение Максвелла для электростатического поля умножим на пробный заряд q 0:
Разность потенциалов – это работа поля по перемещению пробного заряда из начального положения в конечное, отнесённая к модулю этого заряда и взятая с обратным знаком, или работа внешних сил при том же перемещении, отнесённая к модулю пробного заряда.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 139; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.62.10 (0.007 с.) |

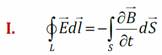
 физический смысл: переменное магнитное поле порождает вокруг себя вихревое электрическое поле.
физический смысл: переменное магнитное поле порождает вокруг себя вихревое электрическое поле.


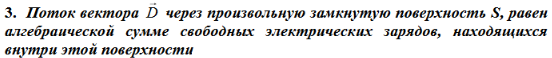

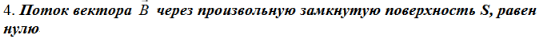
 Здесь ρ – объёмная плотность заряда;
Здесь ρ – объёмная плотность заряда;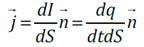 – плотность тока (см. рисунок)
– плотность тока (см. рисунок)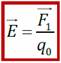 Е – вектор напряженности поля, силовая характеристика поля, равная отношению силы F, действующей на заряд, к величине этого заряда q. В каждой точке пространства в данный момент времени существует своё значение вектора E в разных точках пространства, таким образом, E —- это векторное поле.
Е – вектор напряженности поля, силовая характеристика поля, равная отношению силы F, действующей на заряд, к величине этого заряда q. В каждой точке пространства в данный момент времени существует своё значение вектора E в разных точках пространства, таким образом, E —- это векторное поле.
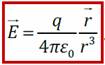 Напряжённость электрического поля точечного заряда
Напряжённость электрического поля точечного заряда
 По тонкому кольцу равномерно распределён заряд Q > 0. Находим напряжённость электрического поля в точке A на оси кольца (OA = z). Разобьём кольцо на точечные заряды dq (на рисунке показаны два малых заряда dq и dq′, равные по модулю и расположенные диаметрально противоположно). По принципу суперпозиции полей – где dE - напряжённость электрического поля малого заряда dq.
По тонкому кольцу равномерно распределён заряд Q > 0. Находим напряжённость электрического поля в точке A на оси кольца (OA = z). Разобьём кольцо на точечные заряды dq (на рисунке показаны два малых заряда dq и dq′, равные по модулю и расположенные диаметрально противоположно). По принципу суперпозиции полей – где dE - напряжённость электрического поля малого заряда dq.
 Величины r и θ (угол) одинаковы для всех элементов dq:
Величины r и θ (угол) одинаковы для всех элементов dq:
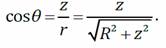 подставим
подставим 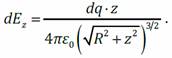

 Введем новую физическую величину, характеризующую электрическое поле – поток вектора напряженности электрического поля (Φ).
Введем новую физическую величину, характеризующую электрическое поле – поток вектора напряженности электрического поля (Φ).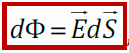


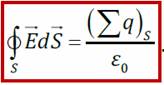

 , где
, где  — поверхностная плотность заряда.
— поверхностная плотность заряда.


 Работа электростатического поля по перемещению пробного заряда по произвольной замкнутой траектории равна нулю. Это означает, что электростатическое поле потенциально. Потенциальная энергия заряженной частицы в электростатическом поле равна работе внешних сил при перемещении этой частицы из точки, где потенциальная энергия принята равной нулю, в данную точку, или работе поля при этом перемещении:
Работа электростатического поля по перемещению пробного заряда по произвольной замкнутой траектории равна нулю. Это означает, что электростатическое поле потенциально. Потенциальная энергия заряженной частицы в электростатическом поле равна работе внешних сил при перемещении этой частицы из точки, где потенциальная энергия принята равной нулю, в данную точку, или работе поля при этом перемещении: 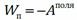 .Потенциальная энергия – характеристика и поля, и заряда:
.Потенциальная энергия – характеристика и поля, и заряда: 

 Потенциалом электростатического поля [ φ ] = В (вольт) называется физическая величина, равная отношению потенциальной энергии заряда q0 в данной точке пространства, к величине этого заряда.
Потенциалом электростатического поля [ φ ] = В (вольт) называется физическая величина, равная отношению потенциальной энергии заряда q0 в данной точке пространства, к величине этого заряда.


