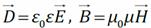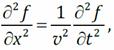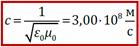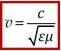Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ферромагнетики. Опыт Столетова. Кривые намагничивания ферромагнетиков. Гистерезис. Точка Кюри. Домены. Качественные объяснения свойств ферромагнетиков.Содержание книги
Поиск на нашем сайте Ферромагне́тики - это вещества, обладающие самопроизвольной намагниченностью, которая сильно изменяется под влиянием внешних воздействий – магнитного поля, деформации, температуры. Магнитная восприимчивость ферромагнетиков положительна и значительно больше единицы.
χ d = d I d H {\displaystyle \chi _{d}={\frac {dI}{dH}}} Из рисунка видно, что кривая χ d {\displaystyle \chi _{d}} начинается при Н = 0 с некоторого конечного значения χ a {\displaystyle \chi _{a}} (начальная восприимчивость) и достигает наибольшего значения χ m {\displaystyle \chi _{m}} (максимальная восприимчивость), соответствующего наиболее крутому подъёму кривой, и затем стремится к нулю, когда намагниченность приближается к насыщению I s {\displaystyle I_{s}}. У каждого ферромагнетика имеется такая температура, называемая точкой Кюри,выше которой это вещество теряет свои особые магнитные свойства.
Петля гистерезиса – график зависимости намагниченности вещества от напряженности магнитного поля Н. Намагниченность Js при H=Hs называется намагниченностью насыщения. Намагниченность ±JR при H=0 называется остаточной намагниченностью (что необходимо для создания постоянных магнитов) Домен — область в ферромагнитном кристалле, в которой существует самопроизвольная намагниченность Уравнения Максвелла для электромагнитного поля в интегральной форме. Переменноеэлектромагнитное поле. Вывод волнового уравнения.
Вывод волнового уравнения для электромагнитных волн Переменное электрическое поле порождает переменное магнитное и наоборот, и это приводит к возникновению электромагнитной волны. Выведем волновое уравнение из I и II уравнений Максвелла в интегральной форме.
Мысленно выделим в пространстве прямоугольные контуры 1234 в плоскости xy и 1456 в плоскости xz, причём ширина контуров Δ x << x. Циркуляция E по контуру 1234:
Циркуляция напряжённости магнитного поля по контуру 1456:
ток смещения сквозь поверхность, натянутую на этот контур,
Общий вид волнового уравнения (для плоской волны)
Скорость распространения электромагнитных волн
скорость распространения электромагнитных волн в вакууме
Скорость электромагнитных волн в среде
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 752; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.009 с.) |

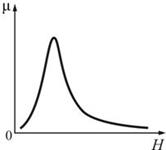 Впервые систематические исследования магнитной проницаемости μ от напряженности Н были проведены Столетовым. Зависимость магнитной проницаемости некоторых ферромагнетиков от напряженности магнитного поля – кривая Столетова.
Впервые систематические исследования магнитной проницаемости μ от напряженности Н были проведены Столетовым. Зависимость магнитной проницаемости некоторых ферромагнетиков от напряженности магнитного поля – кривая Столетова.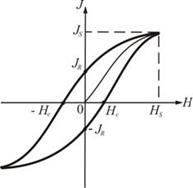 Наличие температуры Кюри связано с разрушением при T>Tk упорядоченного состояния в магнитной подсистеме кристалла – параллельной ориентации магнитных моментов.
Наличие температуры Кюри связано с разрушением при T>Tk упорядоченного состояния в магнитной подсистеме кристалла – параллельной ориентации магнитных моментов. Переменное электромагнитное поле– совокупность изменяющихся во времени и взаимно связанных и обуславливающих друг друга электрического и магнитного полей. Оно определяется двумя векторными величинами – напряженностью электрического поляЕи напряженностью магнитного поля Н.
Переменное электромагнитное поле– совокупность изменяющихся во времени и взаимно связанных и обуславливающих друг друга электрического и магнитного полей. Оно определяется двумя векторными величинами – напряженностью электрического поляЕи напряженностью магнитного поля Н.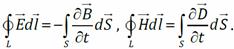
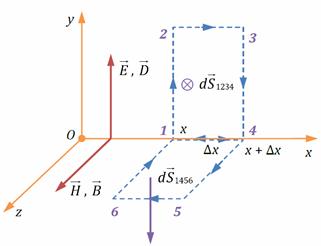 Пусть в пространстве (однородной, изотропной, неферромагнитной среде с относительной электрической и магнитной проницаемостями ε, μ) существует переменное электрическое поле. Свободные заряды и макротоки отсутствуют. Напряжённость электрического поля направлена вдоль оси y и изменяется только вдоль оси x. При этом магнитная индукция будет направлена вдоль оси z:
Пусть в пространстве (однородной, изотропной, неферромагнитной среде с относительной электрической и магнитной проницаемостями ε, μ) существует переменное электрическое поле. Свободные заряды и макротоки отсутствуют. Напряжённость электрического поля направлена вдоль оси y и изменяется только вдоль оси x. При этом магнитная индукция будет направлена вдоль оси z: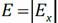 и
и 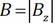
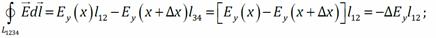
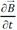 поток сквозь поверхность, натянутую на этот контур, взятый с обратным знаком:
поток сквозь поверхность, натянутую на этот контур, взятый с обратным знаком: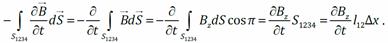 Подставим в I уравнение Максвелла и поделим на Δ x:
Подставим в I уравнение Максвелла и поделим на Δ x: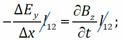 при Δ t → 0
при Δ t → 0 

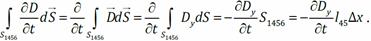 Подставим во II уравнение Максвелла и поделим на Δ x:
Подставим во II уравнение Максвелла и поделим на Δ x: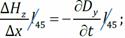 при Δ t → 0
при Δ t → 0 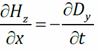 . Т.к.
. Т.к.