
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Магнитное ноле. Вектор магнитной индукции. Сила ампера. Контур с током в магнитном поле. Магнитный момент контура с током.Содержание книги
Поиск на нашем сайте
Магни́тноепо́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения. Основной силовой характеристикой магнитного поля является вектор магнитной индукции B B {\displaystyle \mathbf {B} } (вектор индукции магнитного поля). С математической точки зрения B B = B (x, y, z) {\displaystyle \mathbf {B} =\mathbf {B} (x,y,z)} — векторное поле, определяющее и конкретизирующее физическое понятие магнитного поля. Нередко вектор магнитной индукции называется для краткости просто магнитным полем. Явление электромагнитной индукции – возникновение электрического поля в замкнутом контуре при изменении магнитного потока сквозь поверхность, натянутую на этот контур. ЭДС индукции – энергетическая характеристика этого поля. В замкнутом проводнике, помещённом в переменное магнитное поле, будет создаваться индукционный ток.
Рассмотрим участок проводника длиной dl, находящийся в магнитном поле с индукцией B, по которому идёт ток I. Заряд носителей равен q (будем считать, что в проводнике движутся положительно заряженные частицы), скорость упорядоченного движения – v. На каждый носитель магнитное поле действует
Закон Ампера
Рамка с током в магнитном поле
Вектор магнитного момента показан на 2м рисунке – вид со стороны 23 рамки. Направление магнитного момента выбирается в соответствии с направлением тока в рамке по правилу правого винта. Магнитное поле стремится развернуть рамку с током так, чтобы её магнитный момент был направлен вдоль линий магнитной индукции.
Методы расчета вектора индукции магнитного поля. Закон полного тока для магнитного поля в вакууме. Применение закона к расчету магнитного поля бесконечно длинного прямолинейного проводника с током, тороида и длинного соленоида.
На картинке изображены два провода, по которым текут токи I1 и I2. Вокруг токов имеется контур L. Токи проходят через поверхность, ограниченную контуром L. В качестве положительного направления обхода контура выбираем направление по часовой стрелке. Полный ток – это алгебраическая сумма токов, проходящих через ограниченную замкнутым контуром поверхность.В нашем примере полный ток Σ I есть сумма токов I1 и I2: Σ I = I1 - I2 Знаки токов определяем по правилу буравчика. Теперь найдём магнитное напряжение вдоль контура L. Разбиваем контур на отрезки, которые можно считать прямолинейными, а магнитное поле в месте расположения отрезков однородным. Магнитное напряжение Um для одного такого отрезка длиной ΔL: Um = HL * ΔL Магнитное напряжение вдоль всего контура L: UL = Σ HL * ΔL Полный ток равен магнитному напряжению вдоль контура: Σ I = Σ HL * ΔL Это равенство, установленное экспериментально, и связывает токи с напряженностью их магнитного поля. Магнитное напряжение вдоль замкнутого контура часто называют магнитодвижущей силой. Другое название магнитного напряжения вдоль замкнутого контура – намагничивающая сила. Определение закона полного тока: Магнитодвижущая сила F вдоль замкнутого контура L равна полному току Σ I, пронизывающему поверхность, ограниченную данным контуром. Формула закона полного тока: F = Σ I
Имеется соленоид длиной l с поперечным сечением S, имеющий плотность намотки n (РИС. 26.5). Длина соленоида много больше его поперечных размеров. Найдем индуктивность соленоида.Пустим по соленоиду ток I. Магнитное поле внутри соленоида однородно.
Магнитный поток сквозь один виток соленоида - Потокосцепление -
Тороид – геометрическое тело, образованное вращением плоской фигуры вокруг оси, лежащей в плоскости этой фигуры. Найдем индуктивность тонкого тороида радиуса R, сечением S, имеющего N витков. Пустим по тороиду ток I. Модуль магнитной индукции Магнитный поток сквозь один виток тороида потокосцепление Индуктивность тонкого тороида
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 117; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.195.84 (0.006 с.) |

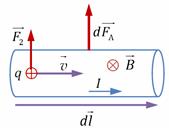 Действие магнитного поля на проводник с током
Действие магнитного поля на проводник с током . Всего на данном участке проводника находится dNносителей заряда, их общий заряд
. Всего на данном участке проводника находится dNносителей заряда, их общий заряд  . Сила, с которой магнитное поле действует на все эти заряды -
. Сила, с которой магнитное поле действует на все эти заряды -  ,
,  ,
,  . Подставляем:
. Подставляем:
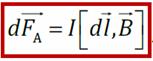 где
где  – сила Ампера – сила, с которой магнитное поле действует на проводник с током.
– сила Ампера – сила, с которой магнитное поле действует на проводник с током.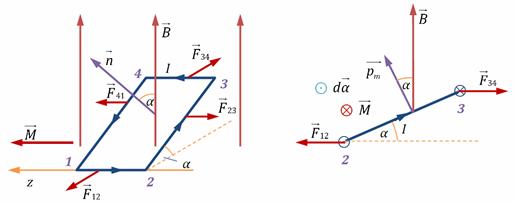 Поместим прямоугольную рамку 1234 с током I в однородное магнитное поле с индукцией; нормаль к плоскости рамки расположена под углом α к линиям магнитной индукции. Равнодействующая сил Ампера, с которыми магнитное поле действует на все четыре стороны рамки, равна нулю, но суммарный момент сил нулю равен не будет – рамка будет разворачиваться вокруг оси, перпендикулярной линиям магнитной индукции. Найдём момент сил Ампера – момент пары сил F 12 и F 34. Пусть ось, перпендикулярная линиям магнитной индукции – ось z проходит через сторону 12. Единственная сила, которая имеет ненулевой момент относительно этой оси, это сила F 34. Её момент
Поместим прямоугольную рамку 1234 с током I в однородное магнитное поле с индукцией; нормаль к плоскости рамки расположена под углом α к линиям магнитной индукции. Равнодействующая сил Ампера, с которыми магнитное поле действует на все четыре стороны рамки, равна нулю, но суммарный момент сил нулю равен не будет – рамка будет разворачиваться вокруг оси, перпендикулярной линиям магнитной индукции. Найдём момент сил Ампера – момент пары сил F 12 и F 34. Пусть ось, перпендикулярная линиям магнитной индукции – ось z проходит через сторону 12. Единственная сила, которая имеет ненулевой момент относительно этой оси, это сила F 34. Её момент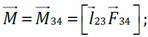
 где где S = l23l34 – площадь рамки;
где где S = l23l34 – площадь рамки; , где
, где 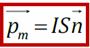 - магнитный момент рамки – характеристика замкнутого проводника (контура) с током (n – нормаль к поверхности рамки); [ pm ] = А·м2.
- магнитный момент рамки – характеристика замкнутого проводника (контура) с током (n – нормаль к поверхности рамки); [ pm ] = А·м2. (Векторный потенциал)
(Векторный потенциал)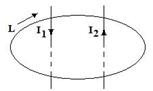 Закон полного тока связывает ток и напряженность магнитного поля.
Закон полного тока связывает ток и напряженность магнитного поля.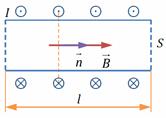 1) Расчёт индуктивности длинного соленоида
1) Расчёт индуктивности длинного соленоида , где n - плотность намотки соленоида/
, где n - плотность намотки соленоида/
 , Индуктивность соленоида -
, Индуктивность соленоида - 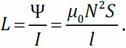
 2) Расчёт индуктивности тонкоготороида
2) Расчёт индуктивности тонкоготороида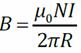
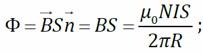

 где где l = 2 πR – длина тороида.
где где l = 2 πR – длина тороида.


