
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работано перемещению проводника и контура с током в магнитом ноле. Явление электромагнитной индукции. Закон ленца. Закон фарадея-максвелла, его вывод из закона сохранения энергии.Содержание книги
Поиск на нашем сайте
Пусть прямолинейный проводник длиной l, по которому идёт ток I, движется в однородном магнитном поле. Магнитное поле действует на проводник с силой Ампера.
Пусть имеется замкнутый проводник с током I, находящийся в магнитном поле. Проводник перемещается из положения 12 в положение 1′2′. Найдём работу магнитного поля по перемещению двух половин этого контура – 12 и 21 по формуле
Явление электромагнитной индукции – возникновение электрического поля в замкнутом контуре при изменении магнитного потока сквозь поверхность, натянутую на этот контур. ЭДС индукции – энергетическая характеристика этого поля. В замкнутом проводнике, помещённом в переменное магнитное поле, будет создаваться индукционный ток. Правило Ленца: направление индукционного тока таково, чтобы компенсировать вызвавшее индукционный ток изменение магнитного потока. Правило Ленца выражается знаком «–» в выражении закона Фарадея-Максвелла.
, dq=Idt,
Это обобщённый закон Ома для замкнутой цепи: сумма падений напряжений равна сумме ЭДС. Обозначим
Явление электромагнитной индукции. Закон Ленца. ЭДС индукции при движении проводника в магнитном ноле. Вывод закона Фарадея-Максвелла на основе электронной теории. Максвелловская трактовка явления электромагнитной индукции. Пepвoe уравнение Максвелла.
Явление электромагнитной индукции – возникновение электрического поля в замкнутом контуре при изменении магнитного потока сквозь поверхность, натянутую на этот контур. ЭДС индукции – энергетическая характеристика этого поля. В замкнутом проводнике, помещённом в переменное магнитное поле, будет создаваться индукционный ток. Правило Ленца: направление индукционного тока таково, чтобы компенсировать вызвавшее индукционный ток изменение магнитного потока. Правило Ленца выражается знаком «–» в выражении закона Фарадея-Максвелла. Явление электромагнитной индукции можно трактовать как возникновение вихревого электрического поля при переменном магнитном поле. Получим закон Фарадея-Максвелла из других опытных законов.
Пусть металлический проводник длиной l движется в однородном магнитном поле B со скоростью v, перпендикулярной линиям индукции. На свободные заряды (электроны) в проводнике магнитное поле действует с силой F2. Из-за этого электроны будут перемещаться по проводнику до тех пор, пока не установится равновесие, т. е. возникшее по этой причине электрическое поле не скомпенсирует воздействие магнитного поля силой F1.Рассмотрим один электрон в проводнике. Он движется с постоянной скоростью – скоростью проводника v, значит, его ускорение равно нулю. Запишем II закон Ньютона:
(Здесь S = lx – площадь поверхности, ометаемой проводником при его движении; S направлен по нормали к этой поверхности.)
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 97; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.147.19 (0.006 с.) |

 Работа при перемещении проводника с током в магнитном поле
Работа при перемещении проводника с током в магнитном поле . Работу будет совершать составляющая этой силы, лежащая в плоскости перемещения проводника,
. Работу будет совершать составляющая этой силы, лежащая в плоскости перемещения проводника, 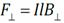 , где B ⏊ – составляющая вектора магнитной индукции, перпендикулярная плоскости движения проводника. Работа магнитного поля по перемещению проводника на малое расстояние dx (соответствующее перемещению)
, где B ⏊ – составляющая вектора магнитной индукции, перпендикулярная плоскости движения проводника. Работа магнитного поля по перемещению проводника на малое расстояние dx (соответствующее перемещению)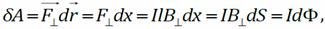 где dS – площадь поверхности, ометаемой проводником при малом перемещении dx (заштрихованная область на рисунке), d Φ – магнитный поток сквозь эту поверхность. При перемещении проводника из положения 1 в положение 2
где dS – площадь поверхности, ометаемой проводником при малом перемещении dx (заштрихованная область на рисунке), d Φ – магнитный поток сквозь эту поверхность. При перемещении проводника из положения 1 в положение 2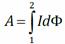 , при I = const работа при перемещении проводника с током
, при I = const работа при перемещении проводника с током 
 Работа при перемещении контура с током в магнитном поле
Работа при перемещении контура с током в магнитном поле .
.
 , где Φ1 – магнитный поток сквозь поверхность, ограниченную контуром 12, Φ2 – контуром 1′2′, Φ0 – контуром 11′2′2
, где Φ1 – магнитный поток сквозь поверхность, ограниченную контуром 12, Φ2 – контуром 1′2′, Φ0 – контуром 11′2′2 здесь ΔΦ = Φ2 – Φ1 – разность магнитных потоков сквозь поверхности, натянутые на проводящий контур в начальном и конечном положении.
здесь ΔΦ = Φ2 – Φ1 – разность магнитных потоков сквозь поверхности, натянутые на проводящий контур в начальном и конечном положении. – закон Фарадея-Максвелла; E i – ЭДС индукции.
– закон Фарадея-Максвелла; E i – ЭДС индукции. Явление электромагнитной индукции можно трактовать как возникновение вихревого электрического поля при переменном магнитном поле. Получим закон Фарадея-Максвелла из других опытных законов.
Явление электромагнитной индукции можно трактовать как возникновение вихревого электрического поля при переменном магнитном поле. Получим закон Фарадея-Максвелла из других опытных законов.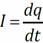 Проводник с током I (ток создаётся источником с ЭДС E) движется в однородном магнитном поле с индукцией, перпендикулярной плоскости движения про- водника. Энергия источника расходуется на совершение механической работы и увеличение внутренней энергии проводника – в тепло:
Проводник с током I (ток создаётся источником с ЭДС E) движется в однородном магнитном поле с индукцией, перпендикулярной плоскости движения про- водника. Энергия источника расходуется на совершение механической работы и увеличение внутренней энергии проводника – в тепло:  . По определению ЭДС, работа источника при прохождении через источник малого заряда dq:
. По определению ЭДС, работа источника при прохождении через источник малого заряда dq:  механическая работа – работа силы Ампера:
механическая работа – работа силы Ампера: 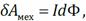 Φ – магнитный поток сквозь поверхность, натянутую на замкнутую цепь, содержа-щую источник и движущийся проводник; количество теплоты, выделяющееся в цепи за время dt прохождения через источник заряда d:
Φ – магнитный поток сквозь поверхность, натянутую на замкнутую цепь, содержа-щую источник и движущийся проводник; количество теплоты, выделяющееся в цепи за время dt прохождения через источник заряда d: 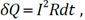 R – сопротивление всей цепи.
R – сопротивление всей цепи. 


 , Это и есть ЭДС индукции.
, Это и есть ЭДС индукции. – закон Фарадея-Максвелла; E i – ЭДС индукции.
– закон Фарадея-Максвелла; E i – ЭДС индукции. Вывод закона Фарадея-Максвелла из электронных представлений
Вывод закона Фарадея-Максвелла из электронных представлений
 где – e – заряд электрона, E – напряжённость электрического поля внутри проводника;
где – e – заряд электрона, E – напряжённость электрического поля внутри проводника; 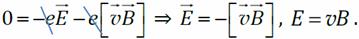 Поле E внутри проводника однородно. Разность потенциалов между концами проводника, по интегральной связи напряжённости и потенциала электростатического поля,
Поле E внутри проводника однородно. Разность потенциалов между концами проводника, по интегральной связи напряжённости и потенциала электростатического поля, 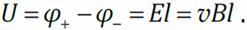 Применим к рассматриваемому проводнику обобщённый закон Ома:
Применим к рассматриваемому проводнику обобщённый закон Ома: 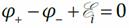 (правая часть этого равенства равна нулю, так как тока в проводнике нет). Отсюда
(правая часть этого равенства равна нулю, так как тока в проводнике нет). Отсюда 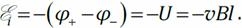 Но v=dx/dt, поэтому
Но v=dx/dt, поэтому 



