
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы теории Максвелла для электромагнитного поля. Уравнения Максвелла в интегральной форме. Их физический смысл.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основы теории Максвелла для электромагнитного поля. Уравнения Максвелла в интегральной форме. Их физический смысл. Поле – любая изменяющаяся в пространстве физическая величина. Электромагнитное поле – поле, действующее на электрически заряженные частицы. Анализируя различные электромагнитные процессы, Максвелл пришел к заключению, что всякое изменение электрического поля должно вызывать появление магнитного поля. Это утверждение является одним из основных положений теории Максвелла и выражает важнейшее свойство электромагнитного поля. Для установления количественных соотношений между изменяющемся электрическим полем и вызываемым им магнитным полем Максвелл ввел в рассмотрение так называемый ток смещения. Это название является условным, а точнее исторически сложившимся, так как ток смещения по своей сути - это изменяющееся со временем электрическое поле. Уравнения Максвелла в интегральной форме
Физический смысл:магнитное поле создаётся не только токамиповодимости, но и изменяющимся во времени электрическим полем.
Физический смысл:оно показывает, что источником электростатического поля являются свободные электрические заряды.
Физический смысл:оно показывает, что в природе не существует магнитных зарядов.
I – сила тока, dS – элементарная площадка, перпендикулярная направлению движения зарядов, t – время Имеются в виду свободные заряды – заряды, нарушающие электронейтральность вещества, и макротоки – упорядоченное движение заряженных частиц, при котором они перемещаются на расстояния, много большие межмолекулярных расстояний. В уравнениях I, II L – произвольная замкнутая кривая, S – произвольная поверхность, ограниченная этой кривой. В уравнениях III, IV S – произвольная замкнутая поверхность, V – объём, ограниченный этой поверхностью. Это фундаментальные уравнения теории электромагнитного поля. Из анализа 1-го и 2-го законов Максвелла следует, что переменное магнитное поле порождает вихревое электрическое, а переменное электрическое поле порождает магнитное, то есть переменные электрическое и магнитное поля неразрывно связаны друг с другом и являются просто проявлениями единого электромагнитного поля. Электростатическое поле. Вектор напряженности поля и методы его расчета. Принцип суперпозиции полей. Примеры расчета напряженности поля методом суперпозиции (кольцо). Электростатическое поле — поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами (при отсутствии электрических токов). Электрическое поле представляет собой особый вид материи, связанный с электрическими зарядами и передающий действия зарядов друг на друга. Если в пространстве имеется система заряженных тел, то в каждой точке этого пространства существует силовое электрическое поле. Оно определяется через силу, действующую на пробный точечный заряд, помещённый в это поле. Пробный заряд должен быть ничтожно малым, чтобы не повлиять на характеристику электростатического поля.Электрическое поле называют однородным, если вектор его напряженности одинаков во всех точках поля. Основные характеристики электростатического поля:напряженность и потенциал
Принцип суперпозиции полей гласит, что напряжённость электрического поля, создаваемого системой заряженных частиц, равна сумме напряжённостей полей, создаваемых каждым из этих зарядов в отдельности. Любую систему заряженных тел можно разбить на точечные заряды (или заряды другой формы, поле которых легко рассчитать) и затем просуммировать (проинтегрировать) напряжённости полей этих зарядов.
Пример расчета напряженности Электрического поля равномерно заряженного тонкого кольца
Векторы напряжённости электрического поля каждого из этих зарядов одинаковы по модулю и направлены так, что концы этих векторов образуют конус с вершиной в точке A (штриховой линией показано основание этого конуса). Проекции этих векторов на плоскость кольца компенсируются, поэтому суммарный вектор направлен вдоль оси z: E (при z > 0). Вычислим Ez. Напряжённость поля точечного заряда:
В этом выражении все величины – постоянные, кроме dq. Проинтегрируем по q:
Поток вектора напряженности. Теорема Остроградского-Гауса для электростатического поля в вакууме. Применение теоремы к расчету напряженности поля. Пример: поле бесконечно большой равномерно заряженной плоскости.
Элементарный поток направлен по внешней нормали к малому участку dS (Если поверхность S не замкнута, то выбор одного из двух направлений нормали произволен, при этом направление нормали для всех участков dS должно быть одинаковым)
Полный поток вектора сквозь поверхность S E
Теорема Остроградского-Гаусса для: поток вектора напряжённости электрического поля сквозь произвольную замкнутую поверхность равен алгебраической сумме зарядов, охваченной этой поверхностью, делённой на ε 0:
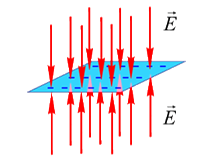
Поле равномерно заряженной бесконечной плоскости: Работа сил электростатического поля по перемещению заряда. Потенциал электростатического поля. Связь между напряженностью поля и потенциалом. Понятие градиента. Методы расчета потенциала. Пример: потенциал на оси равномерно заряженного кольца. I уравнение Максвелла для электростатического поля умножим на пробный заряд q 0:
Разность потенциалов – это работа поля по перемещению пробного заряда из начального положения в конечное, отнесённая к модулю этого заряда и взятая с обратным знаком, или работа внешних сил при том же перемещении, отнесённая к модулю пробного заряда. Потенциал электростатического поля. Связь между напряженностью поля и потенциалом (интегральная и дифференциальная). Примеры расчета потенциала электростатического поля. Диполь в электростатическом поле.
Потенциалом электростатического поля [ φ ] = В (вольт) называется физическая величина, равная отношению потенциальной энергии заряда q0 в данной точке пространства, к величине этого заряда.
Пример расчета напряженности Электрического поля равномерно заряженного тонкого кольца
1. По принципу суперпозиции полей: – где dE - напряжённость электрического поля малого заряда dq. Векторы напряжённости электрического поля каждого из этих зарядов одинаковы по модулю и направлены так, что концы этих векторов образуют конус с вершиной в точке A (штриховой линией показано основание этого конуса). Проекции этих векторов на плоскость кольца компенсируются, поэтому суммарный вектор направлен вдоль оси z: E (при z > 0). Вычислим Ez. Напряжённость поля точечного заряда:
2. Найдём напряжённость электрического поля как функцию z через дифференциальную связь напряжённости и потенциала:
Электрическое поле в веществе. Диэлектрики. Типы диэлектриков. Электронная и ориентационная поляризации. Вектор поляризации и его связь с поверхностными и объемными связанными зарядами. Теорема Остроградского-Гаусса для вектора Р. Проводники – вещества, имеющие свободные заряды – заряженные частицы, свободно перемещающиеся по образцу. Диэлектрики – вещества, в которых заряженные частицы связаны в пределах молекул и могут перемещаться под действием внешнего поля только на расстояния не более межмолекулярных.Любой диэлектрик можно превратить в проводник, т. е. пробить. Сторонние и связанные заряды диэлектрика. Вывод теоремы Остроградского-Гаусса для поля в диэлектрике. Вектор электрического смещения н его связь с напряженностью поля. Диэлектрическая проницаемость вещества. Третье уравнение Максвелла. Сторонние заряды – это заряды, расположенные за пределами диэлектрика, а также заряды, которые хотя и находятся в пределах диэлектрика, но не входят в состав его молекул. Связанные заряды – это заряды, входящие в состав атомов и молекул диэлектрика. Под действием поля они могут лишь немного смещаться из своих положений равновесия. Плотность связанных зарядов равна по абсолютной величине проекции поляризованности на направление внешней нормали рассматриваемой поверхности
– электрическое смещение (электрическая индукция);
- теорема Остроградского-Гаусса для электрического смещения: поток вектора электрического смещения сквозь произвольную замкнутую поверхность равен сумме свободных зарядов, охваченных этой поверхностью.
Где ε- Относительнаядиэлектри́ческаяпроница́емость среды. Относительнаядиэлектри́ческаяпроница́емость среды — физическая величина, характеризующая свойства изолирующей (диэлектрической) среды и показывающая, во сколько раз сила взаимодействия двух электрических зарядов в этой среде меньше, чем в вакууме. Значение ε вакуума равно единице, для реальных сред ε > 1. Для воздуха и большинства других газов в нормальных условиях значение ε близко к единице в силу их низкой плотности. Электрическая постояннаяε0 ≈ 8.85·10−12 Ф/м Третье уравнение Максвелла определяет источники электрического поля. Физический смысл этого уравнения состоит в том, что электрическое поле в некоторой области пространства связано с электрическим зарядом внутри этой поверхности.
Постоянный электрический ток,электростатическое и стороннее поля. Закон Ома в дифференциальной форме. Разность потенциалов, электродвижущая сила и падение напряжения. Обобщенный закон Ома для участка цепи в интегральной форме. График распределения потенциала вдоль участка цепи. Электрический ток -упорядоченное движение заряженных частиц под действием сил электрического поля или сторонних сил. За направление тока выбрано направление движения положительно заряженных частиц. Электрический ток называют постоянным, если сила тока и его направление не меняются с течением времени. Электростатическое поле — поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами (при отсутствии электрических токов). Электрическое поле представляет собой особый вид материи, связанный с электрическими зарядами и передающий действия зарядов друг на друга.Если в пространстве имеется система заряженных тел, то в каждой точке этого пространства существует силовое электрическое поле. Оно определяется через силу, действующую на пробный точечный заряд, помещённый в это поле. Пробный заряд должен быть ничтожно малым, чтобы не повлиять на характеристику электростатического поля.Электрическое поле называют однородным, если вектор его напряженности одинаков во всех точках поля. Основные характеристики электростатического поля:напряженность и потенциал.
Экспериментальный закон Ома в дифференциальной форме: где σ – удельная электропроводность вещества.
Закон Ома справедлив для веществ, в которых концентрация носителей заряда остаётся неизменной.
Закон Ампера
Методы расчета вектора индукции магнитного поля. Закон полного тока для магнитного поля в вакууме. Применение закона к расчету магнитного поля бесконечно длинного прямолинейного проводника с током, тороида и длинного соленоида.
На картинке изображены два провода, по которым текут токи I1 и I2. Вокруг токов имеется контур L. Токи проходят через поверхность, ограниченную контуром L. В качестве положительного направления обхода контура выбираем направление по часовой стрелке. Полный ток – это алгебраическая сумма токов, проходящих через ограниченную замкнутым контуром поверхность.В нашем примере полный ток Σ I есть сумма токов I1 и I2: Σ I = I1 - I2 Знаки токов определяем по правилу буравчика. Теперь найдём магнитное напряжение вдоль контура L. Разбиваем контур на отрезки, которые можно считать прямолинейными, а магнитное поле в месте расположения отрезков однородным. Магнитное напряжение Um для одного такого отрезка длиной ΔL: Um = HL * ΔL Магнитное напряжение вдоль всего контура L: UL = Σ HL * ΔL Полный ток равен магнитному напряжению вдоль контура: Σ I = Σ HL * ΔL Это равенство, установленное экспериментально, и связывает токи с напряженностью их магнитного поля. Магнитное напряжение вдоль замкнутого контура часто называют магнитодвижущей силой. Другое название магнитного напряжения вдоль замкнутого контура – намагничивающая сила. Определение закона полного тока: Магнитодвижущая сила F вдоль замкнутого контура L равна полному току Σ I, пронизывающему поверхность, ограниченную данным контуром. Формула закона полного тока: F = Σ I
Имеется соленоид длиной l с поперечным сечением S, имеющий плотность намотки n (РИС. 26.5). Длина соленоида много больше его поперечных размеров. Найдем индуктивность соленоида.Пустим по соленоиду ток I. Магнитное поле внутри соленоида однородно.
Магнитный поток сквозь один виток соленоида - Потокосцепление -
Тороид – геометрическое тело, образованное вращением плоской фигуры вокруг оси, лежащей в плоскости этой фигуры. Найдем индуктивность тонкого тороида радиуса R, сечением S, имеющего N витков. Пустим по тороиду ток I. Модуль магнитной индукции Магнитный поток сквозь один виток тороида потокосцепление Индуктивность тонкого тороида Явление электромагнитной индукции. Закон Ленца. ЭДС индукции при движении проводника в магнитном ноле. Вывод закона Фарадея-Максвелла на основе электронной теории. Максвелловская трактовка явления электромагнитной индукции. Пepвoe уравнение Максвелла.
Явление электромагнитной индукции – возникновение электрического поля в замкнутом контуре при изменении магнитного потока сквозь поверхность, натянутую на этот контур. ЭДС индукции – энергетическая характеристика этого поля. В замкнутом проводнике, помещённом в переменное магнитное поле, будет создаваться индукционный ток. Правило Ленца: направление индукционного тока таково, чтобы компенсировать вызвавшее индукционный ток изменение магнитного потока. Правило Ленца выражается знаком «–» в выражении закона Фарадея-Максвелла. Явление электромагнитной индукции можно трактовать как возникновение вихревого электрического поля при переменном магнитном поле. Получим закон Фарадея-Максвелла из других опытных законов.
Пусть металлический проводник длиной l движется в однородном магнитном поле B со скоростью v, перпендикулярной линиям индукции. На свободные заряды (электроны) в проводнике магнитное поле действует с силой F2. Из-за этого электроны будут перемещаться по проводнику до тех пор, пока не установится равновесие, т. е. возникшее по этой причине электрическое поле не скомпенсирует воздействие магнитного поля силой F1.Рассмотрим один электрон в проводнике. Он движется с постоянной скоростью – скоростью проводника v, значит, его ускорение равно нулю. Запишем II закон Ньютона: (Здесь S = lx – площадь поверхности, ометаемой проводником при его движении; S направлен по нормали к этой поверхности.) Второе уравнение Максвелла
Второе слагаемое в правой части II уравнения Максвелла – плотность тока смещения.
Причина возникновения электрического тока в неподвижном проводнике - электрическое поле.Всякое изменение магнитного поля порождает индукционное электрическое поле независимо от наличия или отсутствия замкнутого контура, при этом если проводник разомкнут, то на его концах возникает разность потенциалов; если проводник замкнут, то в нем наблюдается индукционный ток. Индукционное электрическое поле является вихревым.
Индукционное электрическое отличается от электростатического поля.
Опыты Г.Герца
Основы теории Максвелла для электромагнитного поля. Уравнения Максвелла в интегральной форме. Их физический смысл. Поле – любая изменяющаяся в пространстве физическая величина. Электромагнитное поле – поле, действующее на электрически заряженные частицы. Анализируя различные электромагнитные процессы, Максвелл пришел к заключению, что всякое изменение электрического поля должно вызывать появление магнитного поля. Это утверждение является одним из основных положений теории Максвелла и выражает важнейшее свойство электромагнитного поля. Для установления количественных соотношений между изменяющемся электрическим полем и вызываемым им магнитным полем Максвелл ввел в рассмотрение так называемый ток смещения. Это название является условным, а точнее исторически сложившимся, так как ток смещения по своей сути - это изменяющееся со временем электрическое поле.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1669; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.71.146 (0.012 с.) |

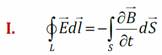
 физический смысл: переменное магнитное поле порождает вокруг себя вихревое электрическое поле.
физический смысл: переменное магнитное поле порождает вокруг себя вихревое электрическое поле.


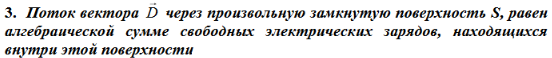

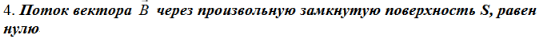
 Здесь ρ – объёмная плотность заряда;
Здесь ρ – объёмная плотность заряда;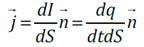 – плотность тока (см. рисунок)
– плотность тока (см. рисунок)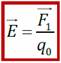 Е – вектор напряженности поля, силовая характеристика поля, равная отношению силы F, действующей на заряд, к величине этого заряда q. В каждой точке пространства в данный момент времени существует своё значение вектора E в разных точках пространства, таким образом, E —- это векторное поле.
Е – вектор напряженности поля, силовая характеристика поля, равная отношению силы F, действующей на заряд, к величине этого заряда q. В каждой точке пространства в данный момент времени существует своё значение вектора E в разных точках пространства, таким образом, E —- это векторное поле.
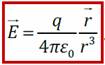 Напряжённость электрического поля точечного заряда
Напряжённость электрического поля точечного заряда
 По тонкому кольцу равномерно распределён заряд Q > 0. Находим напряжённость электрического поля в точке A на оси кольца (OA = z). Разобьём кольцо на точечные заряды dq (на рисунке показаны два малых заряда dq и dq′, равные по модулю и расположенные диаметрально противоположно). По принципу суперпозиции полей – где dE - напряжённость электрического поля малого заряда dq.
По тонкому кольцу равномерно распределён заряд Q > 0. Находим напряжённость электрического поля в точке A на оси кольца (OA = z). Разобьём кольцо на точечные заряды dq (на рисунке показаны два малых заряда dq и dq′, равные по модулю и расположенные диаметрально противоположно). По принципу суперпозиции полей – где dE - напряжённость электрического поля малого заряда dq.
 Величины r и θ (угол) одинаковы для всех элементов dq:
Величины r и θ (угол) одинаковы для всех элементов dq:
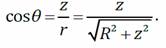 подставим
подставим 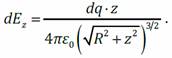

 Введем новую физическую величину, характеризующую электрическое поле – поток вектора напряженности электрического поля (Φ).
Введем новую физическую величину, характеризующую электрическое поле – поток вектора напряженности электрического поля (Φ).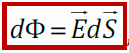


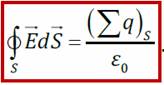

 , где
, где  — поверхностная плотность заряда.
— поверхностная плотность заряда.


 Работа электростатического поля по перемещению пробного заряда по произвольной замкнутой траектории равна нулю. Это означает, что электростатическое поле потенциально. Потенциальная энергия заряженной частицы в электростатическом поле равна работе внешних сил при перемещении этой частицы из точки, где потенциальная энергия принята равной нулю, в данную точку, или работе поля при этом перемещении:
Работа электростатического поля по перемещению пробного заряда по произвольной замкнутой траектории равна нулю. Это означает, что электростатическое поле потенциально. Потенциальная энергия заряженной частицы в электростатическом поле равна работе внешних сил при перемещении этой частицы из точки, где потенциальная энергия принята равной нулю, в данную точку, или работе поля при этом перемещении: 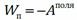 .Потенциальная энергия – характеристика и поля, и заряда:
.Потенциальная энергия – характеристика и поля, и заряда: 

 Потенциалом электростатического поля [ φ ] = В (вольт) называется физическая величина, равная отношению потенциальной энергии заряда q0 в данной точке пространства, к величине этого заряда.
Потенциалом электростатического поля [ φ ] = В (вольт) называется физическая величина, равная отношению потенциальной энергии заряда q0 в данной точке пространства, к величине этого заряда.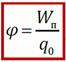
 Разность потенциалов – это работа поля по перемещению пробного заряда из начального положения в конечное, отнесённая к модулю этого заряда и взятая с обратным знаком, или работа внешних сил при том же перемещении, отнесённая к модулю пробного заряда.
Разность потенциалов – это работа поля по перемещению пробного заряда из начального положения в конечное, отнесённая к модулю этого заряда и взятая с обратным знаком, или работа внешних сил при том же перемещении, отнесённая к модулю пробного заряда.
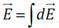 По тонкому кольцу равномерно распределён заряд Q > 0. Находим напряжённость электрического поля в точке A на оси кольца (OA = z). Разобьём кольцо на точечные заряды dq (на рисунке показаны два малых заряда dq и dq′, равные по модулю и расположенные диаметрально противоположно).
По тонкому кольцу равномерно распределён заряд Q > 0. Находим напряжённость электрического поля в точке A на оси кольца (OA = z). Разобьём кольцо на точечные заряды dq (на рисунке показаны два малых заряда dq и dq′, равные по модулю и расположенные диаметрально противоположно).
 Величины r и θ (угол) одинаковы для всех элементов dq:
Величины r и θ (угол) одинаковы для всех элементов dq:
 подставим
подставим  В этом выражении все величины – постоянные, кроме dq. Проинтегрируем по q:
В этом выражении все величины – постоянные, кроме dq. Проинтегрируем по q: 
 .
. 
 Электрический диполь – система двух точечных зарядов, одинаковых по модулю и противоположных по знаку.
Электрический диполь – система двух точечных зарядов, одинаковых по модулю и противоположных по знаку.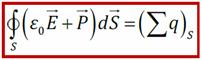 Теорема Остроградского-Гаусса утверждает: п оток вектора напряженности электростатического поля
Теорема Остроградского-Гаусса утверждает: п оток вектора напряженности электростатического поля 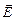 через произвольную замкнутую поверхность
через произвольную замкнутую поверхность 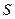 прямо пропорционален алгебраической сумме свободных зарядов, расположенных внутри этой поверхности.
прямо пропорционален алгебраической сумме свободных зарядов, расположенных внутри этой поверхности.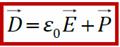
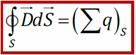
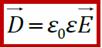 D – это вспомогательная векторная характеристика электрического поля, помогающая расчёту E. Связь напряженности (Е) и вектора электрического смещения (D)
D – это вспомогательная векторная характеристика электрического поля, помогающая расчёту E. Связь напряженности (Е) и вектора электрического смещения (D)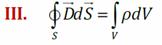
 Большинство проводников подчиняется закону Ома.
Большинство проводников подчиняется закону Ома.

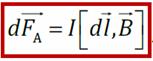 где
где  – сила Ампера – сила, с которой магнитное поле действует на проводник с током.
– сила Ампера – сила, с которой магнитное поле действует на проводник с током. (Векторный потенциал)
(Векторный потенциал)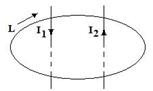 Закон полного тока связывает ток и напряженность магнитного поля.
Закон полного тока связывает ток и напряженность магнитного поля.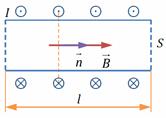 1) Расчёт индуктивности длинного соленоида
1) Расчёт индуктивности длинного соленоида , где n - плотность намотки соленоида/
, где n - плотность намотки соленоида/
 , Индуктивность соленоида -
, Индуктивность соленоида - 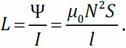
 2) Расчёт индуктивности тонкоготороида
2) Расчёт индуктивности тонкоготороида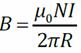
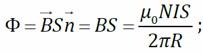

 где где l = 2 πR – длина тороида.
где где l = 2 πR – длина тороида. – закон Фарадея-Максвелла; E i – ЭДС индукции.
– закон Фарадея-Максвелла; E i – ЭДС индукции. Вывод закона Фарадея-Максвелла из электронных представлений
Вывод закона Фарадея-Максвелла из электронных представлений
 где – e – заряд электрона, E – напряжённость электрического поля внутри проводника;
где – e – заряд электрона, E – напряжённость электрического поля внутри проводника; 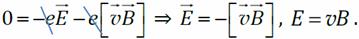 Поле E внутри проводника однородно. Разность потенциалов между концами проводника, по интегральной связи напряжённости и потенциала электростатического поля,
Поле E внутри проводника однородно. Разность потенциалов между концами проводника, по интегральной связи напряжённости и потенциала электростатического поля, 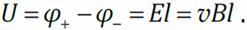 Применим к рассматриваемому проводнику обобщённый закон Ома:
Применим к рассматриваемому проводнику обобщённый закон Ома: 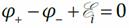 (правая часть этого равенства равна нулю, так как тока в проводнике нет). Отсюда
(правая часть этого равенства равна нулю, так как тока в проводнике нет). Отсюда 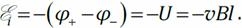 Но v=dx/dt, поэтому
Но v=dx/dt, поэтому 

 Переменное электрическое поле порождает переменное магнитное поле. При этом
Переменное электрическое поле порождает переменное магнитное поле. При этом  .
. Магнитное поле порождается токами:
Магнитное поле порождается токами: 

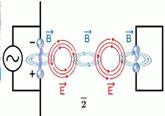
 Генрих Герц в своих опытах попытался создать устройство для изучения электромагнитной волны. Для того чтобы получить излучатель электромагнитных волн, Генрих Герц построил так называемый вибратор Герца, сейчас мы называем его передающей антенной.Рассмотрим, как Генрих Герц получил свой излучатель или передающую антенну.Имея в наличии закрытый колебательный контур (1), Герц стал разводить обкладки конденсатора в разные стороны и, в конце концов, обкладки расположились под углом 1800, при этом получилось, что если в этом колебательном контуре происходили колебания, то они обволакивали этот открытый колебательный контур со всех сторон. В результате этого изменяющееся электрическое поле создавало переменное магнитное, а переменное магнитное создавало электрическое и так далее. Этот процесс и стали называть электромагнитной волной.Если к открытому колебательному контуру подключить источник напряжения, то между минусом и плюсом будет проскакивать искра, что как раз и есть ускоренно движущийся заряд. Вокруг этого заряда, движущегося с ускорением, образуется переменное магнитное поле, которое создает переменное вихревое электрическое поле, которое, в свою очередь, создает переменное магнитное, и так далее. Таким образом, по предположению Герца будет происходить излучение электромагнитных волн. Целью эксперимента Герца было пронаблюдать взаимодействие и распространение электромагнитных волн.
Генрих Герц в своих опытах попытался создать устройство для изучения электромагнитной волны. Для того чтобы получить излучатель электромагнитных волн, Генрих Герц построил так называемый вибратор Герца, сейчас мы называем его передающей антенной.Рассмотрим, как Генрих Герц получил свой излучатель или передающую антенну.Имея в наличии закрытый колебательный контур (1), Герц стал разводить обкладки конденсатора в разные стороны и, в конце концов, обкладки расположились под углом 1800, при этом получилось, что если в этом колебательном контуре происходили колебания, то они обволакивали этот открытый колебательный контур со всех сторон. В результате этого изменяющееся электрическое поле создавало переменное магнитное, а переменное магнитное создавало электрическое и так далее. Этот процесс и стали называть электромагнитной волной.Если к открытому колебательному контуру подключить источник напряжения, то между минусом и плюсом будет проскакивать искра, что как раз и есть ускоренно движущийся заряд. Вокруг этого заряда, движущегося с ускорением, образуется переменное магнитное поле, которое создает переменное вихревое электрическое поле, которое, в свою очередь, создает переменное магнитное, и так далее. Таким образом, по предположению Герца будет происходить излучение электромагнитных волн. Целью эксперимента Герца было пронаблюдать взаимодействие и распространение электромагнитных волн.


