
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поле в однородном диэлектрикеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Необходимо отметить ещё одну важную особенность про-цесса поляризации.
Внутри диэлектрика рядом с положительным зарядом диполя распо-лагается отрицательный заряд соседней молекулы. Поскольку молекулы одинаковые, то сумма этих зарядов равна нулю. Другими словами – заряды диполей внутри диэлектрика взаимно компенсируются. Из рисунка видно, что на поверхности диэлектрика такая компенсация отсутствует – снаружи нет диполей, способных вызвать компенсацию. Поэтому на противоположных поверх-ностях диэлектрика во внешнем электрическом поле возникают нескомпенсированные заряды. Молекулы твёрдого вещества не могут свободно изменять своё положение. Следовательно, нескомпенсированные заряды диполей не могут перемещаться внутри объёма или по поверхности диэлектрика. Поэтому их называют связанными. Связанные заряды, так же как и любые заряды, создают электрическое поле. Это дополнительное электрическое поле всегда направлено против внешнего поля (это видно из рисунка). Поэтому электрическое поле внутри диэлектрика всегда слабее, чем вне его: Е = Е о–
где Е – напряжённость электрического поля внутри диэлектрика, Е ¢ – напряжённость поля связанных зарядов, Е о – напряжённость поля, созданного внешними зарядами.
В соответствии с теоремой Гаусса, напряжённость поля связанных зарядов внутри диэлектрика*
где s¢ – поверхностная плот-ность связанных зарядов. Поверхностную плотность связанных зарядов s¢ можно найти из следующих соображе-ний. В соответствии с опреде-лением поляризованности ди-электрика P полный дипольный электрический момент пласти-ны S р = Р. V. Объём прямоугольной пластины V = S. d (d – толщина плас-тины), поэтому S р = Р. S. d. С другой стороны, полный дипольный электрический момент пластины S р = qd, где q – полный связанный заряд боковой грани пластины, величина которого q = S s¢. Поэтому S р = S s¢ d, и это означает, что Р = s¢, т. е. поляризованность диэлектрика оказывается равной по-верхностной плотности связанных зарядов. Ранее было получено, что поляризованность Р = keо Е, следовательно, теперь можно записать s¢ = keо Е.
________________________
* Это поле, созданное двумя бесконечными равномерно заряженными плос-костями. Учитывая, что
Е = Е о – k Е,
где e = 1 + k – диэлектрическая проницаемость вещест ва. Диэлектрическая проницаемость является безразмерной величиной и показывает, во сколько раз электрическое поле внутри диэлектрика слабее внешнего. В изотропных средах диэлектрическая проницаемость является скалярной величиной.
|
|||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 455; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.216.248 (0.009 с.) |

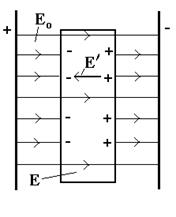
 Под действием внешнего поля положительные и отри-цательные заряды в диэлектрике смещаются. В результате молекулы диэлектрика ориентированы примерно так, как показано на рисунке.
Под действием внешнего поля положительные и отри-цательные заряды в диэлектрике смещаются. В результате молекулы диэлектрика ориентированы примерно так, как показано на рисунке.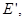
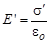 ,
,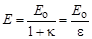 ,
,


