
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка основного закона динамики вращательного движенияСодержание книги
Поиск на нашем сайте
Цель работы: изучить основной закон динамики вращательного движения на маятнике Обербека. Приборы и принадлежности: маятник Обербека, набор грузов для приведения маятника Обербека во вращение, секундомер, штангенциркуль, масштабная линейка.
Описание экспериментальной установки Вращательное движение твердого тела относительно неподвижной оси списывается уравнением
где J – момент инерции твердого тела относительно неподвижной оси; М – проекция момента внешних сил на ту же ось; ε – угловое ускорение. Опытная проверка основного уравнения динамики вращательного движения твердого тела может быть выполнена на маятнике Обербека. Маятник Обербека (рис. 2.1) представляет собой крестообразный маховик, приводимый в равноускоренное вращение падающим грузом Р. Маховик состоит из двух шкивов с радиусами r1 и г2, наглухо скрепленных с четырьмя крестообразно расположенными спицами, вдоль которых перемещаются два дополнительных груза одинаковой массы mгр. Груз Р подвешен на шнуре, который предварительно наматывается на один из двух шкивов мятника Обербека. Шнур со шкива сматывается при падении груза Р. Путь, пройденный этим грузом, отсчитывается по шкале S. Измеряя высоту h несвободного падения груза Р за время t, можно рассчитать ускорение а падения этого груза по формуле
Если шнур при падении груза Р сматывается со шкива без скольжения, то линейное ускорение точек, лежащих на поверхности шкива, равно ускорению груза. Тогда угловое ускорение вращения маховика равно:
где r – радиус шкива, с которого сматывается нить. При движении груза Р на него действуют две силы: сила тяжести mg и натяжения нити Т, под действием которых груз Р падает с ускорением а. Тогда, в соответствии со вторым законом Ньютона, можно написать следующее равенство:
Следовательно, натяжение нити равно:
Под действием натяжения нити маховик маятника Обербека совершает ускоренное вращение. Момент действующей на него силы равен:
Выражение (1.5) получено без учета силы трения, возникающего в оси маятника при его вращении. Уравнение (1.1) в ходе выполнения работы проверяется двумя способами. Первый способ. В этом случае момент инерции маятника фиксирован, а момент сил изменяется. Из уравнения (1.1) имеем
где J0 – момент инерции маятника Обербека при снятых с крестовины грузах. Второй способ. В этом случае неизменными являются масса груза Р и радиус шкива, а значит момент действующей силы не меняется; момент инерции маятника изменяется. Из уравнения (1.1) имеем
Изменить момент инерции маятника Обербека можно, если надеть на стержни маховика грузы mгр и затем изменять их расстояние от оси вращения. Если оба груза mгр находятся на одинаковом расстоянии l от оси вращения и это расстояние значительно больше размеров грузов (тогда их можно считать материальными точками), то их момент инерции можно найти по формуле
Сложив этот момент инерции с моментом инерции маятника без грузов [см. формулу (2.6)], получим момент инерции системы
Измерения Задание 1. Проверить зависимость углового ускорения от момента внешних сил. Выполнение работы начните с измерения высоты h опускания груза Р на нити и радиуса r1 шкива (штангенциркулем). Измерения г1 произвести не менее трех раз и взять за истинную величину среднее арифметическое. Изменить момент сил можно, положив сначала один, затем два и, наконец, три груза на платформу. Массу грузов предварительно определите взвешиванием на технических весах. Для трех значений моментов внешних сил измерить время опускания груза, сделав не менее 4–5 отсчетов. Результаты измерений и расчетов занести в табл. 2.1. Примечание. За массу m принять массу грузов вместе с платформой; масса платформы 50 г ± 0,2 г. По полученным данным убедитесь в справедливости уравнения (2.6) (в пределах ошибок измерения), а, следовательно, и уравнения (2.1). Таблица 2.1
Задание 2. Проверить зависимость углового ускорения от момента инерции (соотношение (2.7)). Момент инерции можно изменять, закрепляя грузы с массой mгр на стержнях симметрично относительно оси вращения на разных расстояниях l от нее. Для каждого момента инерции определите время опускания грузов, делая 4–5 измерений. Примечание. 1. Задание 2 выполняется при постоянном моменте сил (постоянной массе груза на платформе). 2. Масса одного груза на стержне mгр = 89,5 ± 0,5 г. 3. Момент инерции ненагруженного маятника рассчитать как J0ср:
Данные для расчета взять из табл. 2.1. Результаты измерений и расчетов занести в табл. 2.2. Таблица 2.2
Записать результаты измерений с учетом погрешности. Погрешность следует оценивать для найденных отношений. Найдем абсолютные погрешности Относительная погрешность для отношения
Абсолютная погрешность ΔJ1 и ΔJ2 найдем по формуле:
Относительная погрешность для отношения
Абсолютные погрешности получаем умножением относительных погрешностей на вычисленные отношения:
Окончательный результат следует записать в виде:
Относительную и абсолютную ошибки для задания 1 найти самостоятельно и записать результат в виде:
Задание 3. Вычислить момент инерции маятника J0 теоретически, используя определенные формулы для моментов инерции твердых тел различной формы из справочника и сравнить полученный расчетом результат с найденным экспериментально в задании 1. Примечание. Масса стержня 45 г; масса шкива 130 г.
Литература 1. Трофимова, Т. Н. Курс физики / Т. Н. Трофимова. М.: Высшая школа, 2003. 2. Гершензон, Е. М. Механика / Е. М. Гершензон, Н. Н. Малов, А. Н. Мансуров. М.: Академия, 2001. 3. Савельев, И. В. Курс общей физики. В 3 т. Т. 1. / И. В. Савельев. М.: Высшая школа, 1975.
Лабораторная работа № 3
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 2758; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.192.214 (0.006 с.) |


 , (2.1)
, (2.1) . (2.2)
. (2.2)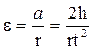 , (2.3)
, (2.3) . (2.4)
. (2.4) . (2.4/)
. (2.4/) . (2.5)
. (2.5) , (2.6)
, (2.6) . (2.7)
. (2.7) . (2.8)
. (2.8) . (2.9)
. (2.9)
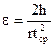 , с–2
, с–2
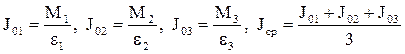 .
. (из (2.6)),
кг×м2
(из (2.6)),
кг×м2
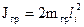 , кг×м2
, кг×м2
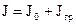 , кг×м2
, кг×м2
 ,
с–2
,
с–2
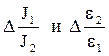 , учитывая, что моменты инерции находили по формуле
, учитывая, что моменты инерции находили по формуле 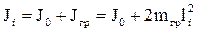 , угловые ускорения – по формуле
, угловые ускорения – по формуле  :
: .
.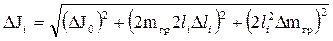 .
.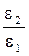 :
: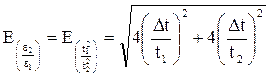 , так как
, так как 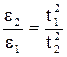 .
. .
.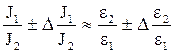 .
.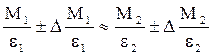 .
.


