
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи теории полезности и подход БайесаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теория полезности – одно из направлений развития методов принятия решений. Смысл данного термина заключается в непротиворечивом количественном описании предпочтений качественных явлений (полезности) и в построении методом логической дедукции полезности сложных комплексов явлений и событий. Принимая решение, руководитель должен выбрать для достижения цели какую-либо возможную линию поведения. В условиях "риска", принимая решение, исходят из того, что некоторые цели, характеризуемые с различной степенью нежелательности, достигаются с различной степенью достоверности при различных линиях поведения. При этом конкретная линия поведения имеет вероятность успеха несколько меньше единицы. Реализация любого решения всегда связана с определенными затратами (денежными, материальными и т.п.), которые можно выразить в количественной форме. Но реализация решения иногда вызывает и другие, не менее важные потери, которые не имеют количественного выражения: снижение авторитета руководителя, нарушение контактов в коллективе, моральные издержки, конфликты и т.п. Теория полезности предусматривает, что результаты какого-либо решения, действия измеряются одним приведенным показателем, называемым полезностью. Полезность рассматривается как некоторого рода обобщенные потери или выигрыш, когда все ценности приведены к одной шкале. На этой шкале можно найти точку, отвечающую определенному событию или исходу. Полезность измеряют в произвольных единицах, называемых единицами полезности, которые можно связать с другими единицами, например, денежными. Эта связь и определяет величину полезности для каждого ЛПР. Человек выбирает тот вариант, который максимизирует полезность в его понимании. Относительные полезности для каждого лица являются измеримыми, а абсолютные – нет. Функция полезности определяется в соответствии с правилом: если человек, принимающий решение, безразличен к выбору между двумя вариантами, то ожидаемая полезность одинакова. ЛПР обычно учитывает установленную им важность различных результатов решений. В некоторые решения входят одновременно количественные и качественные оценки значимости. Например, какую производственную программу целесообразно принять для предприятия? Более напряженную, дающую возможность значительно увеличить прибыль, при условии, что вероятность выполнения напряженной программы - 90 %, или менее напряженную программу, вероятность выполнения которой – 100 %. При выборе вариантов таких решений необходимо учитывать, по возможности, все существенно влияющие факторы, в частности, моральный ущерб при невыполнении плана, как для коллектива, так и для руководителей.
На выбор варианта решения сильное влияние оказывают личные качества руководителя, ведь именно от него зависит выбираемый критерий оценки решений и их предпочтительности. Простейший пример. Вы идете в институт и размышляете: брать с собой плащ (варианта1 ) или не брать (вариант а2). На ваш выбор, безусловно, будут влиять объективные условия: будет дождь (v1) или нет (V2), и поэтому на основе прогноза и оценки ситуации вы из окна определяете (примерно) вероятность дождя. Предположим, вероятность дождяP(V1) = 0,3, тогда вероятность хорошей погодыP(V2) = 0,7. Теперь вы должны дать оценку потерь, т.е. тех неудобств, которые возникнут при различном сочетании вашего решения и погодных условий. Эта оценка не будет одинаковой у разных людей. Один считает, что оказаться без плаща под дождем очень большая неприятность, лучше иметь плащ даже в солнечную погоду, а другие наоборот. Большинство людей будет иметь какое-то среднее мнение. При первом варианте а1 (взять плащ) в случае дождливой погоды оценим неудобство показателем а11 = 1, так как во время кратковременного пребывания на улице дождя может и не быть. Для случая, когда дождя вообще не будет, оценим неудобство показателем а12 = 2. При варианте а2 (не брать плащ), когда дождь может испортить костюм, оценим показателема21 = 7, а для случая, когда дождя не будет (не будет и потерь)а22 = 0. Составим матрицу (табл. 6.5) и выполним кое-какие математические действия.
Таблица 6.5. Матрица линий поведения и объективных условий
Математическое ожидание при выборе каждой линии поведения определяется из выражения:
Ма1 = 0,3 × 1 + 0,7 × 2 = 1,7; Ма2 = 0,3 × 7 + 0 × 2 = 2,1.
Таким образом, чтобы минимизировать ожидаемые потери, необходимо выбрать первую линии поведения (взять плащ). Кроме указанного метода часто используется более простой подход данной теории, применяя метод максимальной ожидаемой полезности:
П = (Ву • Оу) - (Вн • Пн), (6.18)
где П – ожидаемая полезность от принятого решения, Ву – вероятность успеха (удачи), Оу – оценка успеха, Вн – вероятность неудачи, Пн – потери от неудачи. Точность ожидаемой полезности, конечно, будет далеко не абсолютной, но позволит примерно сопоставить варианты по критерию полезности и принять вполне значимое практическое решение. Подход Байеса в принятии решений базируется на разделах теории вероятностей и может применяться в условиях риска, неполной информации и неопределенности. Сущность данного подхода заключается в следующем. На основе своего опыта, знаний, интуиции ЛПР делает предположение относительно возникновения различных ситуаций и их влияния на процесс производства, но его предположения могут значительно отличаться от суждений других специалистов. Применение байесовского подхода позволяет в таких случаях упорядочить различные мнения, выразить количественно имеющуюся неопределенность и на основе этого сделать выводы, которые можно считать вполне приемлемыми /3/. Метод стоимость-эффективность. Данный метод нашел широкое применение в западных странах под названием “затраты - выгоды”. Он включает в себя три этапа: 1 - построение модели эффективности, 2 - построение модели стоимости, 3 - синтез стоимости и эффективности. (Рис. 6.4).
Рис.6. 4. Модель “Стоимость - эффективность”
С помощью этих моделей можно, например, определить эффективное количество выпускаемой продукции по стоимости. Модель стоимости - зависимость общей стоимости выпускаемой продукции от ее количества. Модель эффективности - зависимость вероятности реализации продукции от ее количества. Обе модели расцениваются как объективные. Они строятся на базе фактических данных, надежного статистического материала. Однако, выходные параметры этих моделей не объединяются посредством заданной зависимости. Иногда используется суждение руководителя, который определяет предельные значения стоимости, необходимые значения эффективности. Сопоставив (синтезируя) обе модели, ЛПР принимает окончательное решение.
Метод исследования операций Методы исследования операций (ИСО) возникли в период второй мировой войны и применялись вначале для исследования военных операций. Применительно к производству под “операцией” будем понимать совокупность действий, осуществляемых для достижения определенной цели, например, освоение производства нового изделия, обеспечение производства в соответствии с планом и т.д. Математические методы в ИСО используются как средства достижения результата, т.е. количественные результаты не являются исчерпывающими для решения. ЛПР (как и во всех методах принятия решения) должен учитывать мораль, традиции, привычки и другие социально-психологические факторы. При использовании методов ИСО следует руководствоваться следующим: 1. Учитывать, что деятельность любой подсистемы оказывает влияние на работу других подсистем и всей системы в целом. Поэтому необходимо определять все существенные взаимосвязи и устанавливать их влияние на поведение всей организации в целом. Это так называемый “системный подход”.
2. Проводить исследование силами группы работников, составленной из специалистов различного профиля (инженеров, экономистов, психологов, технологов, математиков и т.п.). Такая группа сможет всесторонне рассмотреть любую задачу с различных точек зрения и выяснить, какой подход или какая комбинация подходов является наилучшей. Следует сказать, что вначале надо испытать различные подходы (технические, экономические, психологические и т.п.) и выбрать наиболее целесообразный из них. Например, перед предприятием стоит задача повышения производительности труда. Как при этом поступят специалисты? Инженер - технолог будет рассматривать проблему с точки зрения совершенствования технологических процессов; организатор - с точки зрения улучшения организации труда, производства и управления, сокращения потерь рабочего времени; экономист - с точки зрения создания системы материальной заинтересованности рабочих в результатах своего труда; социолог и психолог будут заботиться о создании нормального психологического климата в коллективе. Но, что вполне очевидно, наиболее целесообразным будет комплексный подход. 3. Проводить ИСО в тех системах, в которых нельзя по каким-либо причинам осуществлять эксперименты, или если эти эксперименты требуют больших затрат (в том числе, и времени). При этом используют статистические данные, полученные в возможно больших количествах случаев, и на основе анализа этих данных устанавливать функциональные соотношения, связывающие между собой множество переменных, определяющих поведение системы. Исходя из этих соотношений, строится модель, которая имеет форму уравнения. Модели с математической точки зрения могут быть весьма сложными, но структура их довольно проста
Е = f (xi, yi) (6.19)
где Е – мера общей эффективности; f – функция, задающая соотношение между Е, xi, yi; xi – управляемые переменные, определяющие поведение системы; yi – неуправляемые переменные, определяющие поведение системы (действия конкурентов, экономическая обстановка и т.д.). xi – это те факторы, на которые может оказать влияние ЛПР, для чего необходимо определить их перечень и установить значимость каждого фактора. Чтобы найти оптимальное решение с помощью такой модели, надо определить значения управляемых переменных xi, при которых мера общей эффективности будет максимальной. Иногда величина Е может являться мерой неэффективности, например,
Однако, полученное таким образом оптимальное решение не является единственным наилучшим решением реальной задачи, так как сама модель никогда не может быть точным описанием задачи. иначе говоря, степень повышения оптимальности зависит от повышения степени отражения моделью ситуации. Методы разработки математических моделей, их проверка и решение достаточно полно освещены в литературе. Но для их применения и решения требуется серьезная математическая подготовка, которой должны обладать системные аналитики. ИСО находят широкое применение при: · выборе эффективных вариантов использования трудовых ресурсов, оборудования, материалов и денежных средств; · распределении ресурсов, при котором достигается максимальная эффективность производства; оптимизации обслуживания производства (минимизация потерь); · рациональной организации доставки на предприятие материалов и полуфабрикатов; · выборе оптимального маршрута внутризаводского транспорта; · маршрутизации кольцевой системы перевозки грузов. Линейное программирование является методом определения оптимального сочетания ограниченных ресурсов для достижения желаемой цели и считается одним из удачных применений ИСО. Оно основано на предположении, что между переменными xi и yi существует линейная зависимость и можно определить предельное число вариантов путем решения линейных уравнений, благодаря чему возможно найти оптимум в отношении затрат, времени загрузки оборудования и т.п. Наибольшее применение метод линейного программирования получил при решении комплексных проблем, таких, как, производственное планирование (задача Л. В. Канторовича), установление фрахтовых ставок и маршрутов судов, других транспортных средств (транспортная задача), загрузка производственных и складских помещений при наименьших затратах и т.д. Применяются также методы динамического, параметрического, блочного и выпуклого программирования с некоторыми из которых ознакомимся ниже.
9.3. Методы математического программирования и планирования
Успешность решения подавляющего большинства экономических задач зависит от наилучшего, наивыгоднейшего способа использования ресурсов. В процессе экономической деятельности приходится распределять такие важные ресурсы, как деньги, товары, сырье, оборудование, рабочую силу и др. И от того, как будут распределяться эти, как правило, ограниченные ресурсы, зависит конечный результат деятельности, бизнеса Суть методов оптимизации заключается в том, что исходя из наличия определенных ресурсов выбирается такой способ их использования (распределения), при котором обеспечивается максимум (или минимум) интересующего нас показателя. При этом учитываются определенные ограничения, налагаемые на использование ресурсов условиями экономической ситуации В качестве методов оптимизации в экономике находят применение все основные разделы математического программирования (планирования) линейное, нелинейное и динамическое.
Как было сказано ранее (см.9. 2 пособия), линейное программирование является одним из удачных методов применения ИСО. Линейное программирование (планирование) - математический метод отыскания максимума или минимума линейной функции при наличии ограничений в виде линейных неравенств или уравнений. (Линейное здесь означает, что на графике функции изображаются в виде прямых линий, обозначающих 1-е степени соответствующих величин.) Максимизируемая (минимизируемая) функция представляет собой принятый критерий эффективности решения задачи, соответствующий поставленной цели. Она носит название целевой функции. Ограничения характеризуют имеющиеся возможности решения задачи. Существо решения задач линейного программирования заключается в нахождении условий, обращающих целевую функцию в минимум или максимум. Решение, удовлетворяющее условиям задачи и соответствующее намеченной цели, называется оптимальный планом. Линейное программирование (планирование) служит для выбора наилучшего плана распределения ограниченных однородных ресурсов в целях решения поставленной задачи. Если число переменных системы ограничений и целевой функции в математической модели задачи линейного программирования равно двум или трем, то такую задачу можно решать графически или аналитически. При большем числе переменных задачи решают, как правило, аналитическим путем. В общем виде постановка задачи линейного программирования заключается в следующем. Условия задачи представляются с помощью системы линейных уравнений или неравенств, выражающих ограничения, налагаемые на использование имеющихся ресурсов:
где хj - искомые величины, содержащие решение поставленной задачи; аij и bi - известные постоянные величины, характеризующие условия задачи. Целевая функция (линейная форма) задается в виде:
где сj - постоянные коэффициенты (коэффициенты стоимости). Условия задачи (ограничения) могут быть заданы также в виде неравенств. В этих случаях можно привести систему линейных ограничений к виду (6.20), вводя в каждое линейное ограничение дополнительные неотрицательные неизвестные:
X n+1,Xn+2,...,xn+m. (6.22)
Целевая установка оптимизации заключается в том, чтобы свести ожидаемые при решении данной задачи издержки предприятий к минимуму. Общая математическая формулировка задачи соответствует условиям (6.20) и (6.21) Первая строка системы уравнений (6.20)
в данном примере означает следующее а11 - количество единиц ресурсов вида 1 на первом предприятии, а12 - количество единиц ресурсов вида 1 на втором предприятии и т п, b1 - общий ресурс ресурсов вида 1 (для всех предприятий); х1, х2, и т д. - искомое количество предприятий типов 1,2 и т.д. Вторая строка упомянутой системы уравнений содержит аналогичные величины для ресурсов вида 2 и т д Функция цели соответствует формуле (6.21.). Требуется обратить в минимум величину
где с - показатель, характеризующий издержки предприятий. Пусть m - общее число различных видов ресурсов, которыми располагает собственник, an- число типов предприятий, между которыми эти ресурсы должны быть распределены При этом известно, какое количество однородных ресурсов различного вида (i = 1,2…m) может быть реализовано на каждом из предприятий данного типа (j = 1, 2…n), а также общее количество ресурсов данного вида (bi) Известно также относительное значение издержек на каждом из предприятий (сj ). Задача заключается в том, чтобы наилучшим (оптимальным) образом распределить имеющиеся ресурсы по предприятиям, то есть найти неизвестные величины хj - требуемые для этого количества предприятий данного типа. Геометрическая интерпретация задачи линейного программирования возможна лишь при наличии двух независимых переменных. При трех переменных наглядное представление существенно усложняется, так как в этом случае имеет место некоторый выпуклый многогранник в трехмерном пространстве, соответствующий объему допустимых планов. При количестве переменных более трех задача теряет геометрическую наглядность, так как трудно представить себе, например, четырехмерное пространство. Однако идея получения решения, рассмотренного выше, сохраняет смысл и для случая многомерного пространства. На основе этой идеи создан и разработан один из основных методов решения задач линейного программирования – так называемый симплекс-метод. Симплекс-метод является алгебраической формой решения задачи линейного программирования, вытекающей из только что рассмотренного геометрического представления. При обосновании симплекс-метода будем прибегать к уже рассмотренному выше двухмерному случаю, что позволит достаточно просто перейти от геометрического представления к его алгебраической аналогии (см., например, п.8.4./13/). Нелинейное программирование (планирование) — математические методы отыскания максимума или минимума функции при наличии ограничений в виде неравенств или уравнений. Максимизируемая (минимизируемая) функция представляет собой принятый критерий эффективности решения задачи, соответствующий поставленной цели. Он носит название целевой функции. Ограничения характеризуют имеющиеся возможности решения задачи. Целевая функция или хотя бы одно из ограничений не линейны (т.е. на графиках изображаются непрямыми - кривыми - линиями). Существо решения задач нелинейного программирования заключается в том, чтобы найти условия, обращающие целевую функцию в минимум или максимум. Решение, удовлетворяющее условиям задачи и соответствующее намеченной цели, называется оптимальным планом. Нелинейное программирование служит для выбора наилучшего плана распределения ограниченных ресурсов в целях решения поставленной задачи. В общем виде постановка задачи нелинейного программирования сводится к следующему. Условия задачи представляются с помощью системы нелинейных уравнений или неравенств, выражающих ограничения, налагаемые на использование имеющихся ресурсов: Z1(x1,x2,...,xn)>0; Z2(х1,х2,...,хn)>0; ZM(x1,х2,..,xn)>0 при хi > О,
где Z1, Z2,..., Zm - соответствующие функции, характеризующие условие решения поставленной задачи (ограничения); хi — искомые величины, содержащие решение задачи Целевая функция задается в виде:. у=f(х1,x2,...,xn) (6.23) Причем по крайней мере одна из функций у, Z1, Z2...,Zm -нелинейная. Методами нелинейного программирования решаются задачи распределения неоднородных ресурсов. Пусть имеется m разнородных ресурсов, которые предполагается реализовать для бизнеса в n регионах страны. Известны оценочные возможности (вероятности) начать бизнес в j-м регионе (Рj), а также эффективности использования i-го ресурса в n-м регионе (wij). Распределение ресурсов по регионам характеризуется так называемым параметром управления (hij): 0, если i - й ресурс не направляется в j- й регион,}
1, если i - й ресурс направляется в j - й регион.} Необходимо распределить ресурсы по регионам таким образом (выбирать такие значения hij), чтобы величина полной вероятности достижения цели Рц была максимальной. Это ограничение означает, что каждый из т ресурсов обязательно должен назначаться в какой-либо из регионов. Ниже приводится ряд типовых задач, решаемых с помощью нелинейного программирования, которые иллюстрируют его возможности и приемы решения. Нелинейное программирование занимается оптимизацией моделей задач, в которых либо ограничения, либо показатель эффективности (целевая функция), либо то и другое - не линейны. К методам нелинейной оптимизации можно отнести: а) аналитические, использующие методы дифференциального и вариационного исчисления. Они применяются при отсутствии ограничений и при их наличии типа равенства и (или) неравенства; б) численные; в) графические, базирующиеся на графическом представлении функций, подлежащих максимизации или минимизации; г) методы исследования возможных вариантов, основанные на идее генерирования возможных вариантов с целью выбора наилучшего из них; д) экспериментальные (они в настоящее время выделены в новое направление — математическую теорию планирования эксперимента). Пример задачи. При переезде в новый город возникает необходимость доставки к новому месту жительства домашних вещей. При этом известна цена каждой вещи, ее вес и габариты. Количество и вид домашних вещей, которые мы можем увезти, лимитируются грузоподъемностью машины или размерами контейнера. В ходе решения задачи из всего набора предметов выбираются наиболее ценные (с максимальной суммарной стоимостью предметов), вес которых укладывается в грузоподъемность. Задачи нелинейного программирования на практике возникают довольно часто, например, когда затраты растут непропорционально количеству закупленных или произведенных товаров (эффект «оптовости»). Многие нелинейные задачи могут быть приближенно заменены линейными (линеаризованы), по крайне мере, в области, близкой к оптимальному решению. Динамическое программирование (динамическое планирование) представляет собой математический метод оптимизации решений, специально приспособленный к так называемым «многошаговым» (или «многоэтапным») операциям. Многие экономические процессы естественным образом расчленяются на шаги. К ним можно отнести планирование и управление, развиваемые во времени. Шагом в них может быть пятилетка, год, месяц, день. В других операциях разделение на шаги приходится вводить искусственно: например, процесс вывода ракеты на орбиту можно условно разбить на этапы, каждый из которых занимает какой-то временной отрезок. Процесс в данном случае является управляемым, ибо на каждом шаге принимается определенное решение, от которого зависит успех данного шага и операции в целом. Управление как бы складывается из ряда элементарных, «шаговых» управлений. В экономической практике встречаются задачи, которые по постановке и методам решения относятся к задачам динамического программирования: оптимального перспективного и текущего планирования, распределения тех или иных ресурсов, распределения ресурсов и вложения их в производство и т.п. Мы не будем разбирать сложные с математической точки зрения ситуации, а лишь познакомимся с некоторыми отдельными задачами, решаемыми методами динамического программирования. 1.Задача перспективного планирования Планируется деятельность промышленного объединения, состоящего из нескольких предприятий, на период реализации поставленных целей. Необходимо распределить имеющиеся ресурсы, которые в последующем расходуются и получается прибыль. Периодически средства могут перераспределяться. Возникает задача распределения средств между предприятиями, обеспечивающими максимальную прибыль всего объединения.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 489; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.89.140 (0.014 с.) |

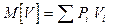 . (6.17)
. (6.17)
 , (6.20)
, (6.20) , (6.21)
, (6.21)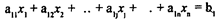 (6.23)
(6.23) (6.24)
(6.24)


