Организация работы с детьми пятого года жизни

В средней группе оказываются обычно дети, перешедшие из предыдущей — второй младшей группы, но нередко в нее вливается часть новых детей, не посещавших ранее дошкольное учреждение. Воспитателю необходимо учитывать особенности состава своей группы и в начале года строить занятия дифференцированно. Программа предусматривает дальнейшее усложнение содержания занятий, поэтому с детьми, только что пришедшими в сад, целесообразно провести ряд занятий по программе предшествующей группы. Да и с детьми, перешедшими из второй младшей группы, часто бывает необходимо вспомнить то, что изучалось в прошлом году, так как за летний период обычно некоторые знания и навыки утрачиваются. В связи с этим целесообразно сентябрь посвятить повторению пройденного программного материала, а к изучению нового приступить несколько позднее.

В средней группе предусмотрено дальнейшее развитие представлений о множестве, размере, форме, о пространственных и временных отношениях, но кроме того, обучение детей счету и начальное формирование понятия числа.

В группе детей пятого года жизни необходимо особо подчеркнуть, что множество может состоять из однородных предметов, но отдельные части его нередко обладают разными качественными признаками, например разных цветов или размеров. Задача состоит в том, чтобы научить детей видеть подмножества данного множества. Это будет подводить детей к пониманию существенных и менее существенных признаков множества как единого целого.

Поскольку дети уже в предшествующей группе научились сравнивать численности множеств, пользуясь приемами наложения и приложения, и определять мощности множеств, у них возникает интерес к счету с помощью слов-числительных.

Во второй младшей группе дети уже начали знакомиться с различными параметрами протяженности и, пользуясь приемом наложения, сравнивать полоски разной длины, ширины, а также

палочки разной высоты, толщины, находить равные и неравные. В данной группе необходимо не только обучить детей приемам подбора равных по длине полосок и палочек, но и подвести к умениям раскладывать их по возрастающей или убывающей длине.

Программа средней группы предусматривает дальнейшее уточнение и более четкую дифференциацию геометрических фигур и их названий. Это вполне доступно детям четырех лет, поскольку в их обиходе имеются различные геометрические фигуры (строительный материал, геометрическая мозаика и ДР-Ь которые они практически различают. В данной группе детей можно познакомить и с некоторыми свойствами этих фигур (устойчивостью и неустойчивостью), а также с их разным размером (малый куб, куб большой, большой круг, круг маленький и т. д.). Очень важно знакомство с формой сразу связывать с количеством и счетом (сосчитать вершины, углы, стороны у той или иной фигуры).

В данной группе надо продолжать учить детей сравнению формы окружающих предметов со знакомыми геометрическими фигурами (лист книги — как прямоугольник, круглый карандаш — как цилиндр и др.).

Все эти знания будут способствовать новому, более глубокому представлению об окружающих предметах. Дети часто радуются тем открытиям, которые они делают якобы сами («У листа бумаги уголки, и у стола уголки, и в комнате есть углы, и у шкафа углы»).

Главное, надо своевременно давать детям такие знания, которые бы обеспечивали развитие наблюдательности и любознательности.

В соответствии с этим и намечены программные задачи.

§ 2. Программный материал для группы детей пятого года жизни

Учить детей различать составные части множества как единого целого; сравнивать их между собой, определяя их равенство и неравенство, не прибегая еще к счету.

На основе сравнения двух совокупностей, расположенных в ряд, друг под другом, учить детей считать элементы каждой из них, определяя равенство и неравенство их числом. Пользоваться при этом правильными приемами счета: называть числительные по порядку, соотносить каждое числительное только с одним предметом, последнее числительное соотносить со всем пересчитанным множеством, например: один, два, три, всего три гуся. Петушков и гусей поровну, по три.

Упражнять в сосчитывании и сравнении двух групп предметов, представленных смежными числами (два и три, три и четы-

ре, четыре и пять). Предметы должны быть расположены в два ряда: один предмет под другим. Дети считают; один, два, три — всего три петушка. Один, два — всего два гриба. Всего три петушка и два гриба. Три петушка больше, а два гриба меньше, значит, три больше, а два меньше.

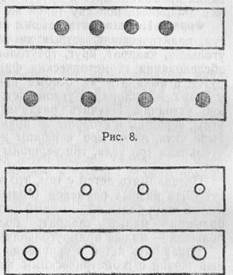
Подвести детей к пониманию того, что количество не зависит от размера предметов и пространственного их расположения. Учить видеть на осноье счета равенство и неравенство чи-сленностей множеств, когда предметы в разных группах находятся на разном расстоя-

нии друг от друга (рис.8).

Учить видеть равенство и неравенство числеино-стей множеств при

условии различных

размеров предметов каждой из групп (рис. 9).

Учить детей отсчитывать, выкладывать, приносить определенное количество предметов по образцу или названному числу, отсчитав из большего количества (например, отсчитай уток столько, сколько я поставила; отсчитай и принеси столько рыбок, сколько кружков на тгоей карточке; отсчитай четыре петушка и три рыбки).

Рис 9.

Учить определять количество предметов по осязанию.

Учить считать звуки.

Учить считать свои движения и движения другого, воспроизводить количество движений по указанному числу. Например, сосчитай, сколько треугольников на твоей карточке, и постучи молоточком по столу столько же раз; хлопни в ладоши пять раз и др.

Учить считать в пределах пяти на числах: один и два; два и два; два и три; три и три; три и четыре; четыре и четыре; четыре и пять; пять и пять (на основе сравнения численностей двух множеств).

Обучать правильному согласованию числительных в роде, числе и падеже. Обучать развернутым ответам: «Я на верхней полоске положил четыре красных кружка, а на нижней полоске три синих кружка. Красных кружков больше, а синих меньше, число четыре больше, чем три, а число три меньше, чем четыре».

Величина. Упражнять в сравнении предметов по протяженности, уменьшая постепенно контрастность их размеров (дать три предмета разных размеров, затем — пять). Учить раскладывать предметы в возрастающем или убывающем порядке по длине, ширине, высоте, толщине. Например, самая длинная, короче, еще короче, еще короче, самая короткая и т. д.

Учить приемам сравнения размеров предметов по их протяженности сначала путем прямого накладывания или прикладывания предметов друг к другу, а затем на глаз, развивая глазомер («Принеси полоску такой же длины» и т. д.).

Форма. Познакомить детей с названиями геометрических фигур, практически известных детям: шар, куб, цилиндр, прямоугольник, квадрат, круг, треугольник. Упражнять в приемах обследования геометрических фигур осязательно-двигательным путем и выявлять их особые признаки: у куба много углов, у шара и цилиндра углов нет; шар и цилиндр катятся, а куб устойчив. Научить различать в геометрических фигурах углы, вершины и стороны. У прямоугольника и квадрата по четыре угла, по четыре вершины и по четыре стороны, а у треугольника три угла, три вершины и три стороны; у круга углов нет.

Познакомить детей с тем, что все геометрические фигуры могут быть разных размеров (большой — малый куб; большой — малый шар; большой — малый цилиндр; большой — малый круг; большой —- малый квадрат; большой — малый треугольник; большой — малый прямоугольник).

Упражнять детей в сравнении форм предметов из окружающей жизни с геометрическими фигурами: карандаш — как цилиндр; тарелка — как круг; лист тетради (книги) — как прямоугольник; чернильница — как куб; мяч — как шар; пионерский галстук — как треугольник, носовой платок—-как квадрат и др.

Упражнять в различении предметов круглой, прямоугольной и треугольной формы. Например, найдите в комнате предметы прямоугольные, квадратные, круглые (крышка стола — прямоугольная, окно — прямоугольное, сиденье стула — квадратное, электрический фонарь — круглый и т. д.).

Ориентировка в пространстве. Уметь показать направление движения от себя (вперед, назад, вверх, вниз, направо, налево) на основе знаний частей своего тела.

Уметь обозначить словами положение того или иного предмета по отношению к себе (впереди меня — стол, позади меня — шкаф, справа от меня — дверь, а слева — окно, вверху от меня — потолок, а внизу — пол).

Знать значение слов ближе — дальше, близко — далеко; пользоваться этими словами (кисточки я положил дальше от себя, а карандаши ближе; направо я наклеил квадрат, налево—' прямоугольник, а круг расположил посередине и др.).

Ориентировка во времени. Закреплять и расширять у детей представление о сутках и их составных частях. Знать, что сутками называется утро, день, вечер и ночь вместе. В сутках четыре части: утро, день, вечер, ночь; знать их последовательность.

Познакомить со сменой суток и выражениями: сегодня, вчера, завтра.

Познакомить со значением слов: быстрее — медленнее, быстро — медленно.

Примерные занятия с множествами и по счету в группе детей пятого года жизни

Формирование представления о множестве.

С детьми четырех лет целесообразно начинать работу так же, как и с детьми трех лет, с формирования представления о множестве. Важно познакомить их с тем, что множество может состоять из частей, научить выделять эти части. Например, в группе много детей, но среди них есть мальчики и девочки. Кого же среди всех детей больше (меньше) — мальчиков или девочек — или их поровну в группе? Можно предложить детям разделиться на две группы — мальчиков и девочек — и встать в два ряда друг против друга. Сравнение рядов покажет, у кого же нет пары: против нескольких мальчиков не стоят девочки. «Значит, мальчиков больше»,— делают вывод сами дети. Итак, в группе детей много, но в это «много» входят девочки и мальчики, и оказалось, что мальчиков больше, чем девочек, части этого «много» неравны.

В группе много разной мебели, например столов и стульев, но при сравнении выяснилось, что стульев больше, а столов меньше. Следовательно, части тоже оказались неравными.

Можно провести и такое занятие. Детям, сидящим за столами, раздаются кружки — каждому трех цветов, в разном соотношении. Например, одному больше всего красных, меньше зеленых и еще меньше синих, другому красных и зеленых поровну, а синих меньше и т. д., т. е. у всех детей будут разные части множества кружков. «Итак, кружков у каждого много, но из каких частей состоит их множество?» — «Из трех частей: красной, зеленой и синей части».— «А можно ли узнать, какая из этих частей больше или меньше? Или все части равны?»

Детям предлагают подумать, как это можно выяснить. Дети припоминают то, что делали ранее. Они уже научились раскладывать предметы в ряд правой рукой, слева направо. Умеют точно расположить кружки друг под другом. Задание детям посильно, и они стараются тщательно его выполнить. Кружки одинакового цвета располагаются рядами так, чтобы каждый кружок одного ряда был под кружком другого ряда. При опросе оказывается, что у всех детей" вышло по-разному: у кого крас-

ных больше, синих поменьше, а зеленых мало; у кого, наоборот, больше всего синих, а красных и зеленых меньше, но их поровну и т. д. В конце такого занятия детям предлагается снова смешать кружки вместе: «Их опять много,— говорит воспитательница.—Но вы знаете, что это множество состоит из разных частей — из кружков красного, синего и зеленого цвета».

Конечно, вначале такое занятие можно упростить, предложив составить множество кружков из двух цветов, и у всех детей красная часть кружков будет больше, чем синяя, и т. д. (упрощение или усложнение задания будет зависеть от уровня

подготовленности детей).

Теперь можно уже отойти от прежней договоренности, о том, что множество должно состоять лишь из однородных предметов (см. стр. 56). Дети учатся видеть, с одной стороны, все целое, обладающее общим признаком, и с другой — его части, которые в свою очередь обладают своими признаками, несущественными для множества в целом; это тоже множества, они входят как части в состав большего множества. Сопоставление элементов двух множеств создает прочную наглядно-чувственную основу для перехода к обучению детей счету с помощью слов-числительных.

Идея конкретного множества близка и может быть доступна самым маленьким детям, если ее сделать предметом их внимания. В самом деле, у них много игрушек, однако это «много» — разное по своему составу. Выделить эти составные части и показать детям взаимосвязь частей с целым очень важно и ценно не только для математического, но и для общего умственного развития детей. Это более ценно, чем спешить учить детей счету, хотя значение обучения счету мы ни в какой мере не снижаем.

Днфференцировка

множеств

и наименование

каждого из них

числительными

(итоговым числом)

на основе счета

воспитателя.

Работу по обучению счету рекомендуется начать со сравнения численностей множеств и различения большей и меньшей из них. Целесообразно, чтобы эти множества различались по своему количественному составу одним элементом. Каждое из множеств дети определяют: одно как большее, а другое как меньшее по численности. Воспитательница указывает, что эти множества могут быть сосчитаны и можно определить число элементов каждого, что дети сами могут научиться считать.

Обучение счету включает как бы две стороны. Одна — это различение большего и меньшего множества и определение количества их элементов числом, которое устанавливается на основе счета элементов, а другая — это сам процесс счета. Если различение множеств и называ-

ние их числом есть цель, то счет — это средство добиться цели, процесс. Целесообразно, чтобы сначала дети усвоили цель счета. Надо раскрыть перед ними эту цель, а затем вооружить надлежащими средствами.

Но поскольку цель и средства взаимосвязаны, а одновременное усвоение их вызывает известные затруднения (они сразу не дифференцируются детьми), эти стороны счетной деятельности временно можно разделить между воспитателем и детьми: процесс счета осуществляет воспитатель, а дети на основе счета воспитателя и умения различать численности множеств называют лишь итоговое число: говорят, сколько элементов всего в том или другом множестве.

Внимание детей в этот период фиксируется прежде всего на сравнении численностей множеств и на основной цели счетной деятельности — итоговом числе.

Для сравнения используются разные множества, выраженные смежными числами. Остановимся на примерных занятиях подобного рода.

Воспитательница, как обычно, на двух свободных полосках раскладывает предметы: три грибка — на нижней полоске и две редиски — на верхней полоске, располагая каждую редиску над грибком. Она объясняет детям, что теперь они будут не только различать, где больше и где меньше предметов, но и говорить, где сколько. Но так как они еще не умеют считать, она будет делать это сама, а дети будут называть, где же сколько. Воспитательница считает грибки, а затем редиски, пользуясь теми приемами, которым будет в дальнейшем обучать детей. «Одна, две — всего две редиски»,— подчеркивает она голосом итоговое число. «Сколько же всего редисок?» — «Две редиски»,— отвечают дети. «Узнаем теперь, сколько грибков: один, два, три, всего три грибка»,— говорит воспитательница и делает ударение на итоге счета. «Сколько же грибков?» — «Три... три... три...»,— раздаются голоса. «Чего три?» — уточняет воспитательница. «Три грибка»,— говорят дети. «А вы запомнили, сколько я сосчитала редисок? (Далеко не все дети сразу запомнили, хотя слышатся отдельные голоса). Я еще раз сосчитаю, а вы запомните, сколько редисок и сколько грибков». Воспитательница считает. Слышны голоса: «Две редиски... три грибка...» — «А посмотрите, чего больше?» — «Грибков».— «А сколько их?» — «Три грибка»,— «А чего меньше?» — «Редисок».— «А сколько их?» — «Две».—■ «Чего две?» — «Две редиски».— «Правильно,— обобщает сама воспитательница,— редисок две, их меньше, а грибков три — их больше. Чего же больше? Подумайте: две редиски или три грибка?» — «Три грибка больше»,— отвечают некоторые дети.

Добавив одну редиску, воспитательница спрашивает: «А что можно сказать теперь про редиски и грибки?» — «Их по-

ровну»,— говорят дети, видя равенство числа элементов. «По скольку же редисок и грибков?» — «По три».— «Я проверю, верно ли, что их поровну, по три?» Воспитательница считает и делает обобщение: «Всего три редиски». Затем также считает грибки и обобщает: «Всего три грибка. Правильно сказали некоторые дети, что редисок и грибков по три, редисок теперь стало столько же, сколько грибков, их три и грибков три. А как же это получилось? Почему их стало поровну, по три, когда редисок было меньше, всего две?» — «Вы положили еще одну редиску, и стало поровну».— «По скольку стало грибков и редисок?» — «По три».— «Почему же грибков осталось по-прежнему три?» — «А вы ничего к ним не добавляли»,— говорят дети. Это очень важный вывод, к которому они приходят сами на основе сравнения двух множеств. Они видят, что с добавлением одного предмета изменяется их количество, а значит, и число.

Далее воспитательница берет другие группы предметов и раскладывает их на тех же двух полосках. Она предлагает детям выяснить, каких предметов больше и каких меньше, вновь считает оба множества, советуя детям запомнить итоговое число. Затем просит детей показать, где два предмета, а где три, образуя ассоциативные связи между «меньшим множеством» и словом-числительным два и между «большим множеством» и словом-числительным три. Поскольку дети ранее много раз сравнивали множества, еще не считая их элементы, и глаз ребенка научился легко различать множества, ассоциативные связи между множествами и числом образуются сравнительно легко, но они возникают не путем лишь восприятия множества и наименования его числом, а на основе того действия счета, которое производит воспитательница. Название числа как показателя мощности множества становится для детей актом суждения, а не простого запоминания, подобно тому как это происходит при усвоении названия того или иного предмета.

Таким образом, усвоение детьми итогового числа на основе счета воспитательницы опирается, с одной стороны, на различение детьми множеств, путем сопоставления элементов, а с другой стороны, на новый способ сосчиты-в а н и я воспитательницей элементов множеств при помощи слов-числительных. Новые знания дети приобретают, опираясь на ранее усвоенные.

Следовательно, при обучении детей счету на первых занятиях нх внимание направляется на сравнение и различение множеств и наименование их словом-числительным — как итоговым числом на основе счета воспитательницы. Дети при этом усваивают, что не все называемые воспитательницей слова-числительные равнозначны. Только последнее названное ею число является итоговым и относится ко всему множеству в

целом. Это весьма важный вывод, который делают дети, и подвести их к нему должен воспитатель.

Например, пересчитав две елки, а под ними стоящие в ряд три грибка, воспитательница спрашивает детей, чего больше: грибов или елок. Дети правильно говорят, что грибов больше, их три, а елок меньше, их две. Запомнив, что елок две, а грибов три, дети смогут ответить на такие вопросы воспитательницы: «Почему же елок меньше, если они по размеру больше грибков (елки высокие, а грибки низкие)?» Дети показывают, что грибов больше, так как один грибок стоит без елки, елок не хватает, их меньше. Значит, два меньше, чем три. «А можно ли сказать, что грибков два? Послушайте, я еще раз посчитаю грибки». Считая, воспитательница называет среди трех числительных н числительное два. Слышны голоса детей: «Нельзя». Но они не могут еще дать объяснение. Вопрос воспитательницы заставляет детей задуматься: некоторые говорят, что надо убрать один грибок, другие говорят, что сначала два, а потом три, значит, три гриба. Не все дети еще до конца понимают, почему, сосчитав один, два, три, нельзя сказать: «А всего —два». Для этого слова-чнслнтельные должны стать понятием числа. Но сама постановка вопроса уже наталкивает ребенка на вывод, что только последнее названное слово-числительное обобщает все множество; оно становится итоговым числом — показателем общего количества элементов; к тому же на основе сравнения они видят, что самих предметов больше во множестве, именуемом три.

Таких занятий, где процесс счета выполняется воспитательницей, не нужно проводить очень много: дети сами начинают выражать желание посчитать множества предметов. Они вторят при счете воспитательнице, как бы помогая ей; заявляют, что они уже сами умеют считать: «Я сам!», «Я умею считать сама» и т. п. Воспитательница поддерживает интерес детей, начинает вызывать тех, кто уже запомнил порядок слов-числительных, однако главным на этом этапе обучения является соотнесение итогового числа со всем множеством.

Нет никакой необходимости спешить в обучении детей процессу сосчитывания: важнее подготовить их к этому этапу. А чтобы навыки счета стали более прочными и сознательными, нужно, чтобы представления детей о множествах, способах их поэлементного сравнения, представления о количественных отношениях множеств, выражаемых разными числами, были содержательными.

Обучение детей счетной операции.

Следующая задача — обучение детей операции счета и углубление их представления о счете как. специфической деятельности людей. Зачем люди считают, что они хотят узнать? Мама считает деньги, когда идет в магазин, она хочет узнать, хватит ли их на покупку. Воспитательница сосчитала конфеты, а потом раздала

их детям поровну и т. д. На таких житейских примерах, на основе собственных наблюдений дети могут быть подведены к тому, что в деятельности счета всегда есть цель —узнать, сколько всего, а сам счет —только процесс для достижения этой цели. Научиться считать, это значит научиться определять общее количество чего-нибудь, например, сколько из большой стопки тарелок надо отсчитать дежурному, чтобы накрыть к обеду тот или иной стол; знать, сколько мячей взяли на прогулку, чтобы вернуть их все в детский сад, и др.

Осознание значения счета как деятельности очень важно — это повысит интерес детей к его усвоению.

Обучать счету можно на таких же занятиях, как указывалось выше (на основе сравнения двух равномощных множеств или когда одно из них «больше другого» на один элемент).

На что важно обратить внимание детей на этом этапе обучения? Основные элементы счета следующие:

а) называние числительных по порядку;

б) соотнесение каждого числительного только с одним предметом множества;

в) усвоение значения итогового числа, т. е. понимание того, что последнее числительное, названное при счете и отнесенное к последнему объекту, в то же время относится ко всему пересчитанному множеству и является показателем общего количества элементов множества.

Цель счетной деятельности — найти итоговое число, а средством достижения этой цели является называние числительных по порядку и соотнесение их к каждому элементу множества. Следовательно, надо продолжать учить детей различать итог счета от процесса сосчитывай и я.

Какие же методические приемы способствуют этому?

При обучении детей операции счета с помощью числительных особую роль играют движения. Счетная операция непременно должна сопровождаться на первых этапах показом рукой на каждый предмет. Движение показа или легкое передвижение предмета, сопровождаемое громким называнием слов-числительных, помогает раздробить множество, более четко выделить каждый элемент. Не меньшее значение имеет и обобщающий жест в виде кругового движения, показывающего, что последнее числительное относится ко всему множеству в целом и является итоговым числом.

Конечно, характер движений постепенно должен изменяться, например, по окончании счета предметы в целом можно передавать другому лицу, сопровождая называнием их общего количества («Вот тебе пять петушков»), или передвигать, переносить [(«Здесь всего четыре елочки») и т. п.

Другим приемом, подчеркивающим значимость итогового числа, является называние его вместе с пересчитываемыми предметами. Например, дети считают зайчиков, против каждого из

которых расположены морковки. «Один, два, три — всего три»,— говорят дети. Воспитательница спрашивает: «Кого три?» — «Три зайчика»,— отвечают дети. «А морковок сколько?» Дети считают: «Одна, две, три — всего три морковки». Наименование предметов вместе с итоговым числом подчеркивает его особое значение, выделяя его из процесса счета.

Упражняясь в сравнении множеств, дети видят, что при их равенстве, как бы эти множества ни были выражены, всегда получаются одинаковые итоговые числа; а если в одной из групп больше на один предмет, получаются смежные числа. Так постепенно дети начинают понимать различия между числами, «Вот два флажка, а здесь три флажка»,— показывает ребенок на каждую из полосок. И тут же, по собственной инициативе передвинув флажок на полоску с двумя флажками, он радостно заявляет: «А теперь здесь стало два, а здесь три флажка. Я сам передвинул его сюда».

Смена наглядного материала приводит детей и к такому важному выводу, что хотя множества бывают составлены из разных предметов (зайцы и морковь, яблоки и вишни и т. д.) разного размера (крупные и мелкие), эти множества могут быть равны; а равенство всегда выражено одним и тем же числом. Так постепенно число становится для детей показателем мощности множества. При этом дети практически убеждаются, хотя и не сразу, что число два всегда больше, чем один, а число один меньше двух, т. е. начинают понимать взаимосвязь между смежными числами — данное число может быть больше одного числа и в то же время меньше другого. А это подводит детей к пониманию относительности понятий больше и меньше, что очень важно для умственного развития.

Следует упражнять детей в преобразовании множеств, например ставить перед ними задачу, как из множества в три предмета сделать множество в два предмета, и наоборот.

В этих упражнениях дети видят, что с добавлением лишь одного элемента к ранее созданному множеству его мощность увеличивается и называется уже иным числом, последующим, а если из прежнего множества удалить один предмет, она станет меньше и будет называться другим — предшествующим числом. При сравнении множеств и назывании их числами необходимо особо подчеркнуть эти взаимно-обратные отношения: два больше одного, но меньше трех; три больше двух, но меньше четырех; пять больше четырех, но меньше шести и т. д. Наглядное сравнение элементов двух множеств, именуемых разными, но смежными числами, будет постепенно подводить детей к пониманию разностных отношений.

Обучение счету должно проводиться на равных и неравных множествах, выраженных числами 1 и 1; 1 и 2; 2 и 2; 2 и 3; 3 и 3; 3 и 4; 4 и 4: 4 и 5: 5 и 5.

Сначала целесообразно ограничиться первыми тремя числами, особенно на первом этапе, до обучения процессу счета, а несколько позднее обучать счету на числах всего первого пятка; при этом особо важно подчеркнуть значение последнего названного числа как итогового.

. Упражнения в счетной операции.

Варианты занятий могут быть разнообразными, но вначале надо опираться на приемы, хорошо известные детям.

Приведем ряд примерных занятий.

Детям даются карточки с двумя свободными полосками для раскладывания на них мелких предметов (кружки, квадраты, треугольники, игрушки и др.) (см. стр- 348). На своем столе воспитательница ставит, например, три елки, предлагает детям сосчитать их, затем просит на верхней полоске выложить столько же красных кружков, сколько у нее стоит елочек. После выполнения данного задания детям предлагается на нижней полоске расположить столько же грибов, сколько кружков на верхней полоске, и сказать, сколько же грибов они выложили. Обращая внимание на елочки, кружки и грибки, воспитательница спрашивает, что можно сказать об их количестве. Дети обычно отвечают: «Елочек, грибов и кружков одинаково».— «А как иначе, более точно, можно сказать об этом?» — ставит вопрос воспитательница, наводя детей на мысль о равенстве. «Все поровну»,— отвечают дети. Или: «Грибов и кружков столько же, сколько елочек».

Вначале дети не сразу делают это обобщение; после вопроса воспитательницы они снова начинают пересчитывать каждое из множеств и лишь на этой основе говорят: «Везде по три». Так наглядно устанавливается взаимно-однозначное соответствие, равномощность множеств, которая отражается в одинаковом числе.

Что в этом занятии нового? Дети считают елочки на столе воспитательницы на расстоянии. Но они сами должны создать равномощное множество из кружков, т. е. знать, что значит «столько же». Вслед за этим дети выкладывают на нижней полоске столько же грибков и находят равенство между численно-стями всех трех множеств, сосчитав их элементы.

Множества, состоящие из сюжетных игрушек, могут заменяться множествами из геометрических фигур: треугольников, кружков, квадратов разного цвета. Меняться должно и расположение количеств на полосках, например, на верхней полоске располагается то больше, то меньше кружков, то одного цвета, то другого; важно, чтобы дети видели, что количество, число не связаны с пространственным расположением или цветом предметов— элементов множества. К тому же смена заданий приучает детей внимательно вслушиваться в указания воспитателя, связывать числа с наименованиями предметов, с их количествами и пространственным расположением совокупностей. Попутно воспи-

тательница обращает внимание детей и на геометрические фигуры, которые служат материалом для счета; например, она предлагает выбрать из коробки треугольники и разложить их на полосках. Такая смена материалов и характера заданий, с одной стороны, необходима для избежания шаблона в действиях детей, а с другой — очень полезна для развития восприятия детей, которое направляется одновременно и на количество, и на форму, и на пространственное расположение предметов.

На одном из занятий детям может быть предложено выкладывать множества не по образцу, а лишь по названному числу. Усложнение здесь состоит в том, что дети должны уже четко представить себе количественную значимость числа. «На верхней полоске положите три синих треугольника, а на нижней четыре красных кружка». Воспитатель следит, чтобы количество было связано с указанными геометрическими фигурами, с их цветом и правильным расположением на полосках. Очень важно, чтобы кружки и треугольники располагались точно друг под другом.

Конечно, все это запомнить удается не сразу: дети не всегда точно связывают количество с предметами, предметы с их цветом и расположением. Поэтому при наличии большого количества ошибок задание следует упростить, например, дать только кружки двух цветов, т. е. ввести меньше признаков, тогда детям надо будет запомнить лишь количество и цвет кружков, а также место расположения данного множества. Если ошибки всего у двух-трех детей, то спешить с исправлением их в процессе работы не следует. Целесообразнее, прослушав два-три правильных ответа, вызвать для ответа и того ребенка, который допустил ошибку. «Послушаем, дети, как выполнил задание Коля. Правильно ли он положил кружки?». Часто ребенок, описывая вслух, как он сделал, сам замечает свою ошибку. «Вы сказали три синих треугольника, а я взял четыре, а кружков красных три. Я ошибся». Если ребенок сам не обнаруживает ошибки, другие дети могут указать на нее.

Подобные занятия приучают детей учиться слушать ответы друг друга, сопоставлять, сравнивать. Постепенно дети усваивают связи между числом, наименованием предметов, их качествами и расположением множеств.

Овладев умениями считать, дети пользуются приобретенными навыками во всех случаях, когда требуется определить количество каких-либо предметов.

В процессе обучения дети должны также усвоить, что множества предметов, выраженные одним и тем же числом, могут быть расположены по-разному. Например, на одной карточке элементы множества расположены на большом расстоянии друг от друга, а на другой — сравнительно близко, хотя количество элементов в том и другом случае одинаково. Считая, дети обнаруживают их равенство. Для проверки данного ра-

венства можно предложить детям закрыть рисунки кружков на одной карточке треугольниками, затем переложить эти треугольники на кружки другой карточки. Так дети практически убеждаются в равномощности множеств. Это утверждает их в значении счета кзк верного средства определения количества.

При проведении занятий можно разнообразить не только материал, но и методические приемы.

Например, в разных местах комнаты расставляются группы игрушек в разном количестве. Нескольким детям дается карточка с нарисованными на ней в ряд предметами или геометрическими фигурами. Им предлагается сосчитать количество предметов на карточке, найти соответствующую по количеству группу предметов и подложить к ней карточку, а затем рассказать, какие это предметы и сколько их в данной группе.

Другой вариант этого занятия. Вызванному ребенку дается не карточка, а группа мелких игрушек, которые он должен сам сосчитать; затем найти в том же количестве группу игрушек, расставленных в комнате, и, подложив к ним свои игрушки, рассказать детям, чего сколько. Чтобы научить детей аргументировать свою правоту, воспитательница спрашивает: «А как ты докажешь, что нашел на столе столько же игрушек, сколько их было у тебя?» Если ребенок сам не догадается, кто-либо из детей поможет ему расставить принесенные игрушки под найденной группой один к одному.

Более сложным вариантом задания будет нахождение количества игрушек по заданному числу. Такое задание могут выполнять одновременно несколько детей: один ищет четыре, другой — три, третий — пять и т. д., т. е. каждый должен найти соответствующую группу лишь по названному числу, не имея количественного образца. Это труднее для ребенка, потому что он должен прочно запомнить число и представить соответствующее количество. Например, ему дано задание найти три игрушки (конкретное наименование предметов не дается). В поисках ответа он подходит к группе из четырех предметов, считает их и отходит, так как помнит, что он должен отыскать три предмета. Продолжая поиски, он останавливается у пяти предметов, считает их и снова отходит. Но бывает так, что счет разных групп вытеснил задание, и ребенок забывает, сколько ему надо отыскать игрушек. Поэтому важно предупредить детей о необходимости запомнить число. Однако, если нужно, воспитательница или другие дети напоминают ребенку о заданном числе.

Что нового в данном типе занятий? Ребенку надо ориентироваться в количестве предметов, не находящихся непосредственно перед ним. Раньше у ребенка в руках был образец, который напоминал ему о количестве (карточка с нарисованными предметами или мелкие игрушки), а теперь он должен помнить только заданное ему число. В поисках же соответствующего Количества он встречается с разными совокупностями, которые

отвлекают его внимание, и не сразу находит нужное. Это затруднение упражняет его волю, воспитывает целеустремленность, сосредоточенность, упражняет память.

Подобные занятия проводились и во второй младшей группе, когда дети отыскивали «один» и «много» в специально организованной обстановке, но теперь содержание их усложнено.

Обучение приемам

Отсчитывания

Предметов.