Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функціонально-істиннісні відношення між судженнями.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
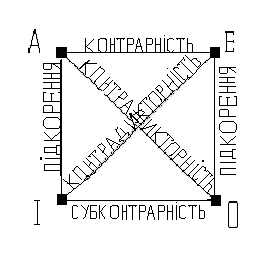
Між судженнями мають місце логічні відношення, насамперед, за їх істиннісними значеннями. Це стосується як простих, так і складних суджень. Відношення між простими судженнями визначаються, з одного боку, їх логічною формою: характером суб’єкта, предиката і логічних операторів, а з другого — їх смислом. Спочатку розглянемо, які відношення існують між атрибутивними судженнями. За своїм змістом атрибутивні судження можуть перебувати у відношеннях порівнюваності і непорівнюваності. Непорівнювані судження мають або різні суб’єкти, або різні предикати, або одночасно різні суб’єкти і різні предикати. Наприклад, у судженнях: «Всі автомобілі — це транспортні засоби, що рухаються по суходолу» і «Собака є живою істотою» різними є суб’єкти і предикати. У непорівнюваних судженнях істинність або хибність одного судження не залежить від істинності або хибності іншого. Тому їх подальший логічний аналіз не здійснюється. Порівнювані судження мають однакові суб’єкти і предикати, але можуть відрізнятися одне від одного за кількістю і якістю. Їх можна зіставляти між собою за матеріальним (істиннісним) значенням. За своєю логічною формою порівнювані судження поділяються на сумісні і несумісні. Сумісні судження містять одну й ту саму думку (повністю або частково). Між ними виникають такі логічні відношення: еквівалентності, підпорядкування, часткового збігу (перетину). Еквівалентні (рівнозначні) судження можуть бути лише або разом істинними, або разом хибними. В еквівалентних судженнях суб’єкти і предикати є тотожними за смислом поняттями (хоча слова, якими ці поняття позначаються, можуть бути різними). Наприклад: «Всі прокурори — юристи» і «Всі судові обвинувачі мають юридичну освіту». Несумісні судження містять різні якості (одне судження стверджувальне, інше — заперечне). Між несумісними судженнями можуть існувати логічні відношення: контрарності (протилежності), субконт-контрарності (перетину) і контрадикторності (суперечності). Відношення підпорядкування, часткового збігу, контрарності (протилежності) і контрадикторності (суперечності) спостерігаються між судженнями видів: А, Е, І, О. їх часто відображують у вигляді логічного квадрата. Логічний квадрат – це штучна схема, яку запропонували ще середньовічні схоласти. Дамо схему логічного квадрату:
Між судженнями видів А — І, Е — О існують відношення підкорення (підпорядкування). У цих суджень якість термінів однакова, а кількість — різна. Тут існує лише одна закономірність. З істинності підпорядковуючого судження (А для І) та (Е для О) випливає істинність підпорядкованого йому судження (І для А) та (О для Е). Адже існує правило: «все, що є істинним для цілого класу предметів буде істинним для частини цього класу». Наприклад: Всі собаки — живі істоти (істинне, виду А). Деякі собаки — живі істоти (істинне, виду І). Всі дерева – не тварини (істинне, виду Е). Деякі дерева – не тварини (істинне, виду О). Між судженнями видів І — О існує відношення субконтрарності (часткової сумісності). Це означає, що вони не можуть бути одночасно хибними, але можуть бути одночасно істинними. Тобто із хибності одного із них випливає істинність іншого, але не навпаки. Наприклад: Деякі грабіжники — не злочинці (хибне, виду О). Деякі грабіжники — злочинці (істинне, виду І). Деякі люди є студентами (істинне, виду І). Деякі люди не є студентами (істинне, виду О). Між судженнями видів А — Е існує відношення контрарності (протилежності). Це означає, що вони не можуть бути одночасно істинними, але можуть бути одночасно хибними. Наприклад: Всі люди мають автомобілі (хибне, виду А). Всі люди не мають автомобілів (хибне, виду Е). Між судженнями видів А — О, Е — І (діагоналі квадрата) наявні відношення контрадикторності (суперечності). Це означає, що вони не можуть бути одночасно істинними і не можуть бути одночасно хибними. Наприклад: Всі люди є юристами (хибне, виду А). Деякі люди не є юристами (істинне, виду О). Всі тигри не є собаками (істинне, виду Е). Деякі тигри є собаками (хибне, виду І). Подамо наочно типи відношень, що існують між простими атрибутивними судженнями видів А, Е, І, О у таблиці.
Релятивні судження мають багато спільного з атрибутивними (зокрема, їхні суб’єкти теж мають кількість і якість). Тому між релятивними судженнями також існують відношення: повної або часткової сумісності, підпорядкування, протилежності, суперечності, логічної незалежності тощо, наприклад, загально-одиничне стверджувальне судження («Всі х R у1», «Всі українські міста менші ніж Київ») перебуває у відношенні підпорядкування до частково-одиничного стверджувального судження («Деякі х R у1», «Деякі українські міста менші ніж Київ»). У зв’язку з обмеженістю обсягу посібника систематично ці відношення ми розглядати не будемо. На відміну від атрибутивних, релятивні судження мають не одномісний предикат, а n-місний (2-місний і більше), тому відношення між релятивними судженнями мають свою специфіку, щодо атрибутивних. Розглянемо специфічні для релятивних суджень відношення: симетричності й несиметричності, транзитивності і нетранзитивності, рефлексивності і нерефлексивності, які виникають залежно від характеру відношення «R » між суб’єктами: «х» та «у». Симетричними (від грецьк. sуттеtrіа — співмірність) називають відношення між суб’єктами: «х» та «у», коли немає значення, який із них йде першим, а який наступним. Тобто зміна порядку їх розташування не може впливати на смислове й матеріальне (істиннісне) значення таких суджень. Відношення симетрії має місце у судженнях про рівність («5 + 7 = 4 + 8»), подібність («іспанська мова подібна до італійської»), одночасність («Микола їде в метро і в цей самий час Василь читає книгу») тощо. Деякі відношення можуть бути або не бути симетричними залежно від типу суб’єктів. Наприклад, відношення «братерство» (між братами воно є симетричним, а між братом і сестрою – ні. Наприклад, у судженні «Микола є братом Андрія» має місце відношення симетричності, оскільки вони однакові між собою як брати, тому той же самий смисл має судження «Андрій є братом Миколи»). Але, якщо ми кажемо, що «Микола є братом Тетяни», то тут відношення не є симетричним. Адже ми не можемо сказати, що «Тетяна є братом Миколи» (вона є його сестрою). Несиметричними називають відношення між суб’єктами: «х» та «у», коли важливий порядок їх розташування, бо зміна порядку може вплинути на смислове або матеріальне значення таких суджень. Наприклад, якщо ми стверджуємо, що судження «Степан є батьком Миколи» є істинним, то це не означає, що ми стверджуємо істинність судження «Микола є батьком Степана» (Микола — не батько Степана, а його син). Несиметричними будуть відношення: «більше», «менше», «важче», «легше», «раніше», «пізніше» та ін. Транзитивні (перехідні) (від лат. trаnsіtus — перехід) відношення мають місце між двома (або більше) суб’єктами тоді, коли з одного відношення між суб’єктами: «х» та «у», та іншого відношення між суб’єктами: «у» та «z», ми можемо перейти до відношення між суб’єктами: «х» та «z», зберігаючи те ж саме відношення. Наприклад, якщо «х»еквівалентне «у», а «у»(в свою чергу) еквівалентне «z», то це значить, що «х»еквівалентне «z». Це можуть бути також відношення між різними математичними величинами: відношення «більше», «менше», «важче», легше» та ін. Наприклад, з відношень: «8>6» і «6>4», ми можемо зробити перехід до відношення: «8>4». Транзитивними також будуть відношення між відрізками часу («раніше», пізніше», «одночасно»), частинами простору («вище», «нижче») тощо. У нетранзитивних (неперехідних) судженнях ми не можемо з одного відношення між суб’єктами: «х» та «у», та іншого відношення між суб’єктами: «у» та «z», перейти до відношення між суб’єктами: «х» та «z», зберігаючи те ж саме відношення. Наприклад, якщо істинним буде судження «Ніканор — батько Романа» і також істина — «Роман є батьком Марії», то це не значить, що істинним буде судження «Ніканор — батько Марії», оскільки у нашому прикладі Ніканор буде дідом Марії. Рефлексивні (від лат. rеflехіо — відображення) відношення характеризуються тим, що кожний із членів відношення «R»між суб’єктами: «х» та «у»перебуває у такому ж відношенні «R» до самого себе. Рефлексивними є, наприклад, відношення одночасності, рівності та ін. Наприклад, якщо «4x3=12», то «4x3=4x3» і «12=12». Нерефлексивні відношення характеризуються тим, що кожний із членів відношення «R»між суб’єктами: «х» та «у»не перебуває у такому ж відношенні «R» до самого себе. Наприклад, з істинного, судження «2<5», не виходить, що істинними будуть судження: «2<2» та «5<5». Складні судження також можуть перебувати між собою у певних відношеннях. Але для цього прості судження, з яких вони складаються, повинні містити спільні суб’єкти і предикати. Складні судження бувають порівнювані або непорівнювані. У непорівнюваних судженнях, у простих судженнях, з яких вони складаються, різними є всі предикати і суб’єкти, тому такі судження неможливо зіставити за смислом й аналізувати їх співвідношення за істинністю чи хибністю. Наприклад, маємо таке складне судження, в якому між простими відсутній смисловий зв’язок: «Петро вкрав 10 гривень і був затриманий» або «Микола пішов на лекцію з логіки, а після неї поїхав додому». У порівнюваних судженнях, у простих судженнях, з яких вони складаються, можуть бути спільні суб’єкти, але різні предикати, або можуть бути спільні предикати, але різні суб’єкти, і можуть бути спільні і предикати, і суб’єкти. Порівнювані судження бувають сумісні і несумісні, між ними можуть бути ті самі типи відношень, що й між простими атрибутивними. Сумісні судження бувають еквівалентними, частково сумісними і підпорядковуючими. Несумісні судження бувають протилежними (контрарними) і суперечливими (контрадикторними). Еквівалентні судження бувають або одночасно істинними, або одночасно хибними. За допомогою еквіваленції часто формулюють закони логіки та перетворюють одні судження на інші. Підпорядковуючі судження характеризуються тим, що за умови істинності підпорядковуючого судження підпорядковане завжди буде істинним, але не навпаки. Частково сумісні судження не можуть бути одночасно хибними. Протилежні (контрарні) судження не можуть бути одночасно істинними. Суперечливі (контрадикторні) судження не можуть бути одночасно істинними і не можуть бути одночасно хибними. Наприклад, судження «А» («люди є живими і мислячими істотами») і «ùА» («невірно, що люди є живими і мислячими істотами») є між собою суперечливими. Відобразимо відношення, які існують між складними судженнями: «Р» і «Q», у вигляді таблиці (закреслені рядки означають те, що такі судження не можуть набувати цих істиннісних значень одночасно).
6. Логічні операції над судженнями:
В цьому пункті ми розглянемо трансформацію простих і складних суджень. Трансформація суджень потрібна тоді, коли необхідно з’ясувати їх точний логічний смисл. Ця мета досягається за допомогою таких логічних операцій, як обернення, перетворення, протиставлення суб’єкту і протиставлення предикату.
а) трансформація простих атрибутивних суджень Обернення (конверсія) — це логічна операція над судженнями, що полягає у перестановці місцями суб’єкта і предиката. У результаті такої операції над простими атрибутивними судженнями виникають такі наслідки: Загально-стверджувальні судження (виду «А») можуть обернутися або на частково-стверджувальні (виду «І»). Наприклад, судження «Всі адвокати (S) — юристи (Р)» обертається на судження «деякі юристи (S) — адвокати (Р)». Це так зване обернення з обмеженням. Або ж загально-стверджувальні судження (виду «А») обертаються на загально-стверджувальні (виду «А»). Наприклад, судження «Всі неділі (S) є сьомими днями тижня (Р)» обертається на загально-стверджувальне судження «Всі сьомі дні тижня (S) є неділями (Р)». Це так зване чисте обернення. Частково-стверджувальні судження можуть обернутися на частково-стверджувальні. Наприклад, судження «Деякі автомобілісти (S) обіймають відповідальні державні посади (Р)», обертається на судження «Деякі відповідальні держслужбовці (S) є автомобілістами (Р)». Або ж частково-стверджувальні судження обертаються на загально-стверджувальні судження. Наприклад, «Деякі злочинці (S) — грабіжники (Р)», обертається на судження «Всі грабіжники (S) є злочинцями (Р)». Загально-заперечні судження обертаються на загально-заперечні. Наприклад, «Всі тигри (S) — не мавпи (Р)» обертається на судження «Всі мавпи (S) — не тигри (Р)». Частково-заперечні судження не обертаються. Перетворення (обверсія) — це логічна операція над судженнями, яка полягає у зміні його якості на протилежну. Її можливість ґрунтується на тій обставині, що подвійне заперечення дає ствердження. За допомогою такої операції над судженнями можна отримати наступні результати: Загально-стверджувальні судження (судження виду «А») перетворюються на загально-заперечні судження (виду «Е»). Формула «Всі S є Р» = «Жоден S не є не Р». Наприклад: «Всі тигри — хижаки» = «Жоден тигр не є нехижак». Навпаки, загально-заперечні судження (судження виду «Е») перетворюються на загально-стверджувальні судження (виду «А»). Формула «Жоден S не є не Р» = «Всі S — Р». Наприклад: «Жодний фокстер’єр (S) не є несобакою (Р)» = «Всі фокстер’єри (S) — собаки (Р)». Частково-стверджувальні судження (судження виду «І») перетворюються на частково-заперечні судження (судження виду «О»). Формула: «Деякі S є Р» = «Деякі S не є не Р». Наприклад: «Деякі студенти (S) є автомобілістами (Р)» = «Деякі студенти не є неавтомобілістами». Навпаки, частково-заперечні судження (судження виду «О») перетворюються на частково-стверджувальні судження (судження виду «І»). Формула: «Деякі S не є Р» = «Деякі S є не Р». Наприклад: «Деякі вчені не є фізиками» = «Деякі вчені є нефізиками». Протиставленням суб’єкту називають трансформацію суджень, коли над судженням спочатку роблять операцію обернення, а потім операцію перетворення. Наведемо приклад такої операції. Маємо таке судження: «Всі футболісти — спортсмени», в результаті обернення отримаємо судження: «Деякі спортсмени — футболісти», а в результаті наступного перетворення отримаємо судження: «Деякі спортсмени не є нефутболістами». Протиставленням предикату називають трансформацію суджень, коли над судженням спочатку роблять операцію перетворення, а потім операцію обернення. Наведемо приклад такої операції. Маємо таке судження: «Жоден студент не є не людиною», в результаті операції перетворення отримаємо судження: «Всі студенти — люди», а в результаті операції обернення отримаємо судження: «Деякі люди — студенти».
б) трансформація простих релятивних суджень Ці судження, як і прості атрибутивні, підлягають таким основним логічним операціям, як обернення і перетворення. Трансформація релятивних суджень потрібна тоді, коли необхідно з’ясувати їх точний логічний смисл того відношення, на якому вони ґрунтуються. Тобто тоді, коли необхідно знати, чи є воно симетричним або несиметричним, транзитивним або нетранзитивним, рефлексивним або нерефлексивним. Обернення. Якщо відношення «R»є симетричним, то обернення зведеться до простої перестановки місцями суб’єктів цього судження: «х» та «у».Саме ж відношення «R»залишається тим самим. Прикладом може служити всім відоме правило арифметики: «Від перестановки місцями доданків сума не змінюється» (5+7=7+5). Але якщо відношення «R»не є симетричним, то обернення передбачає не лише перестановку місцями суб’єктів цього судження: «х» та «у», а й заміну самого відношення «R»іншим (як правило, протилежним за смислом). Важливо, щоб смисл судження залишався тим самим, а змінювалась би лише його логічна форма. Наприклад, «Київ більший від Житомира = Житомир менший від Києва». Якщо відношення «R»є транзитивним, то обернення судження передбачає обов’язкову заміну цього відношення на протилежне йому за смислом. Наприклад, «Якщо Київ більший від Житомира, а Житомир більший від Радомишля, то Київ більший від Радомишля». І, відповідно, якщо «Київ більший від Радомишля», то «Радомишль менший від Києва». Але якщо відношення «R»не є транзитивним, то обернення судження передбачає не просто заміну цього відношення на протилежне йому, а пошук якогось нового відповідного відношення. Ми вже наводили приклад: якщо «Ніканор — батько Романа» і «Роман — батько Марії», то це значить, що «Ніканор буде дідом Марії». Таким чином, можна вивести закономірність: «Батько мого батька — мені не батько, а дід, отже, я йому не син (дочка), а онук (онука)». Перетворення також має специфіку, якщо його застосовувати до релятивних суджень. У випадку із симетричними судженнями, в результаті їх перетворення отримаємо судження з подвійним запереченням висхідного. А подвійне заперечення у логіці дорівнює ствердженню. Саме ж відношення «R»залишиться незмінним. Наприклад, «6+3=2+7» — це те ж саме, що й «неправильно, що неправильно, коли 6+3=2+7». Але якщо відношення «R»не є симетричним, то перетворення судження передбачає не лише його подвійне заперечення (що дорівнює простому ствердженню), а й заміну самого відношення «R»іншим (як правило, протилежним). Наприклад, якщо правильно, що Дмитро народився раніше за Степана, то неправильно, що неправильно те, що Степан народився пізніше за Дмитра. Над релятивними судженнями можна проводити й інші типи логічних операцій (протиставлення суб’єкту і протиставлення предикату тощо), але оскільки вони зводяться до розглянутих вище (є лише їх комбінаціями), ми не аналізуватимемо їх.
в) трансформація складних суджень Через рівнозначність (еквівалентність) ми можемо із одних складних суджень отримувати інші. Розглянемо основні типи таких перетворень. Кон’юнкцію можна перетворити на звичайну (не строгу) диз’юнкцію, оскільки заперечення кон’юнкції еквівалентне диз’юнкції заперечень. Формула: ~(АÙВ)«(~АÚ~В). Наприклад, «Якщо і тільки якщо неправда, що Сергій є киянином і українцем, то неправильно, що Сергій є киянином, або неправильно, що Сергій є українцем». Диз’юнкцію можна перетворити на кон’юнкцію, оскільки заперечення диз’юнкції еквівалентне кон’юнкції заперечень. Формула: ~(АÚВ)«(~АÙ~В). Наприклад, «Якщо і тільки якщо неправда, що сьогодні субота або неділя, то неправда, що сьогодні субота, і неправда, що сьогодні неділя». Імплікацію можна перетворити на кон’юнкцію, оскільки імплікація еквівалентна запереченню кон’юнкції антецедента (умови імплікації) і запереченню консеквента (наслідку імплікації). Формула: (А®В)«~(АÙ~В). Наприклад, судження «Якщо і тільки якщо вірно, що, коли Семен підготується, то складе іспит з логіки, то невірно, що Семен підготується й не складе іспит з логіки». Імплікацію можна перетворити на диз’юнкцію, оскільки імплікація еквівалентна диз’юнкції заперечення антецедента (умови імплікації) і консеквента (наслідку імплікації). Формула: (А®В)«(~АÚВ). Наприклад, «Якщо і тільки якщо сьогодні Іван складе іспит з логіки, то поїде відпочивати буде істинним лише тоді, коли не вірно, що сьогодні Іван складе іспит з логіки або поїде відпочивати». Можливі й інші перетворення складних суджень (наприклад, кон’юнкцію і диз’юнкцію можна перетворити на імплікацію). Завдяки перетворенню одних складних суджень на інші (еквівалентні їм) ми можемо будувати безпосередні умовиводи, також можна спрощувати складні судження, використовуючи одні логічні сполучники замість інших. Цю можливість широко використовують у сучасній математичній логіці (насамперед у логіці висловлювань). Еквівалентність суджень встановлюється (і перевіряється) за допомогою методу таблиць істинності.
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 1153; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |