Опосередковані дедуктивні умовиводи із простих суджень.

 

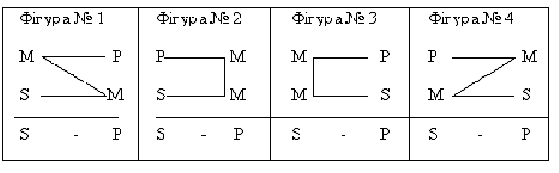
Опосередковані дедуктивні умовиводи будуються або з простих (атрибутивних або релятивних) суджень, або з складних суджень, або є їх комбінаціями. Розглянемо спочатку ті, що складаються лише із простих атрибутивних суджень. У свою чергу, такі умовиводи, залежно від кількості засновків (двох або більше) поділяються на простий категоричний силогізм (ПКС) і складний категоричний силогізм (СКС) або полісилогізм.

а) логічна характеристика простого категоричного силогізму (ПКС)

Опосередковані дедуктивні умовиводи почав досліджувати ще Аристотель. Насамперед йому належить заслуга у виокремленні і дослідженні простого категоричного силогізму (надалі завжди будемо записувати скорочено - ПКС). Слово «силогізм» із грецької мови перекладається як вивід, умовивід або міркування. Слово «категоричний» означає, що ми можемо точно визначити значення істинності суджень, з яких він складається (істина або хиба), слово «простий» позначає ту обставину, що він складається із простих (елементарних) суджень і є у структурному плані порівняно простим стосовно до інших умовиводів.

Отже, ПКС є системою трьох взаємопов’язаних суджень виду: А (Всі S є P), Е (Всі S не є P), І (Деякі S є P), О (Деякі S є P).

Розглянемо загальну структуру ПКС:

1. Перший засновок (судження виду А або Е, або І, або О).

2. Другий засновок (судження виду А або Е, або І, або О).

3. Висновок (судження виду А або Е, або І, або О).

Детальне розуміння ПКС передбачає розуміння змісту наступних понять: термін, фігура, модус силогізму.

Під термінами ПКС мається на увазі суб’єкти і предикати засновків і висновку умовиводу. Для прикладу розглянемо наступний силогізм:

1. Всі лауреати нобелевської премії – видатні особистості.

2. Деякі люди є лауреатами нобелевської премії.

3. Деякі люди – видатні особистості.

Більшим терміном є предикат висновку (у нашому прикладі – слова «видатні особистості»).

М еншим терміном є суб’єкт висновку (у нашому прикладі – слово «люди»).

Середнім терміном є той термін, який входить лише у засновки, і якого немає у висновку (у нашому прикладі – слова «лауреати нобелівської премії»).

Більшим засновком ПКС є той засновок, що містить більший термін.

Меншим засновком ПКС є той засновок, що містить менший термін.

Більший і менший засновки ПКС можна міняти місцями, що не вплине на істиннісне значення висновку.

В залежності від розташування середнього терміну, розрізняють 4 фігури ПКС:

Перша фігура характеризується тим, що середній термін у ній займає місце суб’єкта у більшому засновку і місце предиката у меншому засновку.

Друга фігура характеризується тим, що середній термін у ній займає місце предиката у більшому і у меншому засновках.

Третя фігура характеризується тим, що середній термін у ній займає місце суб’єкта у більшому і у меншому засновках.

Четверта фігура характеризується тим, що середній термін у ній займає місце предиката у більшому засновку і місце суб’єкта у меншому засновку.

Представимо загальну схему для всіх чотирьох фігур ПКС:

 

Де S – суб’єкт засновку;

Р – предикат засновку;

M – середній термін.

Ми бачимо із схеми, що висновок ПКС у всіх чотирьох фігурах полишається незмінним: S - Р.

Окрім фігур виділяють і модуси (від лат. слова modus – спосіб, різновид) ПКС, тобто такі їх схеми, в яких фіксується не лише фігура, а і конкретний вид (А, Е, І або О) засновків і висновків.

Візьмемо для прикладу модус ЕІО 1. Перша літера у ньому (Е) вказує на вид більшого засновку, друга (І) - на вид меншого засновку, а третя (О) – на вид висновку. Цифра вказує на вид фігури. Наведемо приклад конкретного міркування, яке відповідало б даному модусу:

Представимо для початку його схему:

1. Всі М не є Р

2. Деякі S є М

3. Деякі S не є Р

Тепер підставивши замість символів конкретні значення (необхідно пам’ятати, що слово «деякі» береться не у значенні «лише деякі, а не всі», а у значенні «деякі, але, можливо, і всі»), отримаємо такий умовивід:

1. Всі крокодили не є тиграми.

2. Деякі тварини є крокодилами.

3. Деякі тварини не є тиграми.

Аналогічним чином можна було б проілюструвати й інші модуси ПКС.

Висновок логічно правильного модусу ПКС є логічно достовірним, за умови наявності істинних засновків. Іншими словами, ми гарантовано отримаємо істинний висновок у логічно правильному модусі ПКС, якщо його засновки будуть представлені істинними судженнями. Висновок у логічно неправильному модусі ПКС, може бути як істинним так і хибним, навіть якщо його засновки будуть представлені істинними судженнями.

Розглянемо для прикладу 2 модуси ПКС: ААА 1, ААА 2. Спробуємо визначити, який із них є логічно правильним, а який є логічно неправильним:

Розпишемо спочатку структуру модусу ААА 1, а потім підставимо замість символів конкретні значення:

1. Всі М є Р (1. Всі вчені є людьми.)

2. Всі S є М (2. Всі фізики є вченими.)

3. Всі S є Р (3. Всі фізики є людьми.)

Для більшої наочності ми можемо представити дану структуру у вигляді кіл Ейлера:

 

Ми можемо побачити, що даний модус ПКС відповідає принципу побудови дедуктивних умовиводів, оскільки у ньому рух знання відбувався від загального до часткового. Отже, даний модус ПКС є логічно правильним.

Натомість модус ААА 2 є логічно неправильним, щоб довести дане положення розпишемо його структуру і підставимо у неї конкретні значення:

1. Всі Р є М (1. Всі студенти є людьми.)

2. Всі S є М (2. Всі викладачі є людьми.)

3. Всі S є Р (3. Всі викладачі є студентами.)

Також можемо представити його схему, використовуючи кола Ейлера:

 

Ми бачимо, що висновок даного умовиводу не є логічно достовірним навіть за умови наявності істинних засновків. Він може бути як істинним, так і (переважно) хибним, залежно від того, які значення ми будемо підставляти у структуру замість символів. Отже, даний модус ПКС є логічно неправильним.

Логічно неправильні модуси ПКС порушують принцип побудови дедуктивних міркувань (від більш загального – до менш загального), а також правила побудови ПКС. Таких правил нараховують сім:

1. У силогізмі повинні бути лише 3 (не більше, і не менше) терміни.

2. Середній термін повинен бути розподілений хоча б одному із засновків.

3. Якщо більший або менший терміни не розподілені у засновках, то вони не можуть бути розподіленими у висновку.

4. Із двох заперечних засновків не можливо зробити певного висновку.

5. Якщо один із засновків заперечний, то висновок повинен бути заперечним.

6. Із двох часткових засновків певного висновку зробити не можливо.

7. Якщо один із засновків частковий, то і висновок повинен бути частковим.

Існують 256 теоретично можливих модусів ПКС, але, як ми вже вияснили, далеко не всі вони є логічно правильними, оскільки не відповідають принципу побудови дедуктивних міркувань (від більш загального – до менш загального), а також порушують правила побудови ПКС. Всього нараховують 24 логічно правильних модусів ПКС, 19 з яких є «сильними», а 5 – «слабкими». Слабкий модус відрізняється від аналогічного йому сильного тим, що у його висновку замість кванторного слова «всі» наявне кванторне слово «деякі».

Представимо таблицю для правильних модусів ПКС, які гарантують отримання істинних висновків із істинних засновків:

 

	1 фігура ПКС	2 фігура ПКС	3 фігура ПКС	4 фігура ПКС
сильні модуси	ААА; ЕАЕ; АІІ; ЕІО.	ЕАЕ; АЕЕ; ЕІО; АОО	ААІ; ІАІ; АІІ; ЕАО; ОАО; ЕІО.	ААІ; АЕЕ; ІАІ; ЕАО; ЕІО.
слабкі модуси	ЕАО; ААІ.	АЕО; ЕАО.		АЕО

 

б) складні, скорочені і складноскорочені силогізми побудовані із простих категоричних суджень: полісилогізми, ентимеми, епіхейреми, сорити

Окрім ПКС існують й інші дедуктивні умовиводи, які складаються із простих атрибутивних категоричних суджень. Це складні категоричні силогізми (полісилогізми), скорочені (ентимеми) або складноскорочені силогізми (епіхейреми і сорити).

Складним категоричним силогізмом (або полісилогізмом від гр. poly – багато) називають поєднання двох або більше ПКС, в якому висновок одного ПКС (т. зв. просилогізму) є одночасно засновком іншого ПКС (т. зв. епісилогізму).

 

Наприклад:

1. Всі розумні істоти повинні вміти логічно міркувати.

2. Всі люди – розумні істоти.