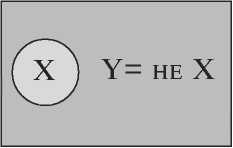Лекція 1. Предмет, значення, історія логіки як науки

Лекція 1. Предмет, значення, історія логіки як науки

План:

Предмет і значення логіки як науки.

Мислення і мова.

3. Історія розвитку логіки як науки:

а) розвиток логічних знань в Античну добу;

б) Середньовічна (схоластична) логіка;

в) логіка у Новий час;

г) прогрес логіки у ХІХ-ХХ століттях;

д) розвиток логіки в Україні.

 

Мислення і мова.

Абстрактно-теоретичне мислення людини суттєво відрізняється від чуттєво-емпіричних форм відображення дійсності: відчуття, сприйняття, уявлення. Чуттєві форми властиві не лише людині, а й іншим живим істотам.

Відчуття – перша елементарна форма чуттєвого відображення реальності. Предмети і явища навколишньої дійсності впливають на сенсорний апарат людини, викликаючи у неї п’ять видів відчуттів: зорові, дотикові, слухові, смакові і нюхові. На їх основі виникають сприйняття, які не є лише їх механічною сукупністю.

Сприйняття – це цілісні синтетичні образи зовнішніх речей. На базі відчуттів і сприйняттів виникають уявлення.

Уявлення з’являються на основі минулих сприйняттів предметів, образи яких збереглися у пам’яті людини.

Людина може уявити собі (у своїх фантазіях) і те, що ніколи не існувало (наприклад, химер, кентаврів або русалок). Проте, як вказав ще англійський філософ Дж.Локк, елементи, з яких складаються такі уявлення-фантазії, беруться людиною з попереднього досвіду (той же кентавр є фантастичною істотою, в якій поєднались ознаки і коней, і людей (він одночасно є напівлюдиною і напівконем), а коней і людей ми можемо спостерігати у навколишній дійсності).

Як правило відчуття нас не підводять і дають точну інформацію про стан справ у навколишній дійсності. Але інколи даних відчуттів самих по собі виявляється недостатньо. Наприклад, якщо ми бачимо зображення рибок на телевізійному екрані, то це не означає, що там насправді знаходяться вказані живі істоти. Крім того, частина відчуттів залежить від стану органів чуттів певної людини і організму у цілому. Буває ж так, що сьогодні певна їжа або вино здається нам приємним на смак, а наступного дня – гіркими. Самі по собі їжа і вино не змінилися, змінилися ми, змінився стан нашого організму.

Людина відрізняється від тварин, насамперед тим, що у своєму відношенні до дійсності, покладається не лише на свої відчуття, але й на мислення. Шимпанзе, можна навчити осмислено використовувати певну кількість слів мови глухонімих. Користуючись такою мовою, шимпанзе може побудувати навіть цілу фразу, наприклад, попросити апельсин або банан. Використання мови є яскравим свідченням того, що певні зародки абстрактного мислення наявні і у вищих тварин, але це все-таки зародки і не більше. Тварини мислять чуттєвими образами (певними комплексами відчуттів), між якими встановлюються асоціативно-психологічні зв’язки. Проте відчуття, сприйняття і уявлення відображають лише зовнішні ознаки та властивості речей. Сутність речей здатна пізнати завдяки своєму мисленню лише людина. Сумнівно, наприклад, що навіть вищі тварини зможуть зрозуміти, що є спільного між механічними, електронними, пісочними, сонячними і т. п. годинниками. Але будь-яка людина, що здатна мислити абстрактно (відволікаючись від зовнішніх чуттєво даних характеристик предметів), легко усвідомить ту обставину, що всі ці предмети мають спільну властивість – вони є хронометрами (приладами призначеними для вимірювання часу).

Люди (так само як і інші вищі живі істоти) можуть думати і не використовуючи слова – мислити образами (на практиці, переважно, так і відбувається), але люди не можуть безпосередньо передавати свої образи іншим людям подібно до того, як з одного комп’ютера можна передати зображення на інший. Тому, передаючи свої думки, ми неодмінно використовуємо мову, яка є свого роду матеріальною оболонкою думки. Саме за допомогою мови відбувається перехід від чуттєвих форм відображення дійсності до абстрактного мислення, здійснюється формування узагальненої думки. Позначаючи словами певні предмети, ми відволікаємось від їх особливостей, від нескінченої кількості їх властивостей. Сутність абстракції і полягає в тому, що відволікаючись від другорядних, ми концентруємо увагу на головних властивостях об’єктів.

Логіку не цікавить мислення окремої людини, логіку цікавить мислення узагальнене і правильне. Мислення однієї людини для іншої людини є свого роду «чорною скринею». Ми не можемо простежити процес формування і розгортання людського мислення безпосередньо. Мислення одного індивіда (суб’єктивне) стає доступним для сприйняття іншого (інтерсуб’єктивним) тоді, коли воно оформлене у мові. Римський оратор Цицерон порівнював мову із тілом, а мислення із душею. Жива людина – це єдність тіла і душі. Мова без мислення – це труп. Мислення без мови – це дух, який не можна вловити.

Мови є звуковими або письмовими (графічними) інформаційними знаковими системами. Мови бувають усними і письмовими. Вони дають можливість закріпити і зберігати людські знання, передавати їх із покоління в покоління.

Існувало і існує більше восьми тисяч природних (національних) мов. Окрім природних, існують штучні мови, які використовуються для виконання спеціальних завдань в окремих науках (наприклад, мовою алгебри ми можемо передати певне обчислення: 6 + 4 = 10). Штучні мови необхідні, насамперед, для того щоб наочно представити структуру того чи іншого предмета або явища. Наприклад, маємо слово «вода» і хімічну формулу «H₂O» у якій наочно показано, що молекула звичайної води складається із одного атому кисню і двох атомів водню, на відміну від молекул важкої і легкої води, у яких атомів водню, відповідно, три (для важкої) і один (для легкої).

Національні мови, на відміну від штучних мов наук, мають ту перевагу, що вони є більш універсальними. Видатний логік Г.Фреге порівнював штучні мови із національними за аналогією із мікроскопом і людським оком. Навряд чи хтось із людей відмовився б від своїх очей на користь мікроскопу, оскільки у повсякденному житті від нього користь незначна. Але мікроскоп стає незамінним, коли необхідно роздивитися структуру певного мінералу або провести мікробіологічний аналіз. Так само, і потреба у використанні штучної мови виникає, насамперед, тоді, коли необхідно розглянути логічну структуру того чи іншого судження або умовиводу. Штучна мова – це свого роду «логічний мікроскоп», за допомогою якого логіки проводять свої дослідження.

Для того, щоб розробити формалізовану логічну теорію, необхідно розробити алфавіт для штучної мови, висхідні положення теорії запровадити у вигляді аксіом, визначити основні правила виведення інших положень із аксіом (наприклад, modus ponens).

Штучна мова для логіки є найголовнішим засобом для аналізу думок, розкриття їх структури. Основний метод логіки – формалізація заснований на широкому впровадженні штучної мови.

 

 

Лекція 2. Поняття як форма мислення

План:

Логічна характеристика поняття, як форми абстрактно-теоретичного мислення.

2. Види понять.

Відношення між поняттями.

4. Логічні операції над поняттями:

а) визначення понять;

б) обмеження і узагальнення понять;

в) поділ понять.

 

 

Види понять.

 

У логіці розрізняють види понять, насамперед, за обсягом: за кількістю елементів обсягу, за характером елементів обсягу й за типом елементів обсягу. Крім того виділяють види понять і за характером ознак, що складають зміст поняття.

За кількістю елементів обсягу поняття поділяють на пусті і непусті.

Пусті (порожні, нульові) — це поняття, в обсязі яких немає жодного елемента. Тобто в реальній дійсності (словосполучення «реальна дійсність» не є тавтологією, оскільки дійсність може бути не лише реальною, але й, наприклад, віртуальною) не існує предмета, який би мав вказану ознаку. Інакше кажучи, обсяг таких понять дорівнює нулю. Прикладами таких понять можуть бути «дев’ятий день тижня», «квадратне коло», «планета Сонячної системи, орбіта якої розташована між орбітами Землі і Марса» тощо. Порожні поняття іноді поділяють на логічно порожні і фізично порожні. Логічно порожні поняття містять ознаки, які внутрішньо суперечливими (наприклад, «число, яке одночасно ділиться і не ділиться на 2»), відповідно існування предметів, які б містили ці ознаки є принципово неможливим. Фізично порожні поняття не містять суперечливих ознак, тому їх обсяг є потенційно непустим, і в реальності могли б існувати предмети, які відповідали б цим ознакам (наприклад, «українське місто із кількість населення більш, ніж шість мільйонів людей»).

Непусті (непорожні) поняття у своєму обсязі містять елементи, тобто в реальній дійсності існують предмети, які мають вказану у понятті сукупність ознак. Непусті поняття поділяють на одиничні й загальні.

Одиничні — це поняття, в обсязі яких існує лише один елемент (наприклад, «засновник логіки» тощо). Дуже часто одиничні поняття є іменами предметів, наприклад, «річка Дніпро», «Ейфелева вежа» тощо. Тим самим, вони виконують функцію іменування предметів, адже лише одиничні поняття відповідають першому принципу теорії іменування.

Загальні — це поняття, обсяг яких складається з двох або більше предметів (наприклад, «автомобіль», «злочинець», «планета» і т. ін.). Загальні поняття, у свою чергу, поділяють на загальні реєструючі і загальні нереєструючі.

У загальних реєструючих поняттях ми можемо чітко зазначити кількість предметів обсягу. Наприклад, обсяг поняття «область України» є загальним і складається з 24 елементів; обсяг поняття «студент групи ОБ 21» станом на 11.04.2011 складається з 29 елементів тощо.

У загальних нереєструючих поняттях ми не можемо чітко зазначити кількість предметів, що входять до їх обсягу. Як правило, ця кількість постійно змінюється, що робить недоцільним такий обрахунок. Наприклад, навіть якщо ми порахуємо кількість беріз, обсяг поняття «береза» буде змінюватися настільки швидко, що вже через місяць їхня кількість буде вже зовсім іншою.

За характером елементів обсягу поняття поділяються на збірні й незбірні.

Збірні — це поняття, в обсязі яких узагальнюються не окремі предмети, а множини предметів, що мисляться як окремі елементи (одиниці) обсягу («група студентів», «ліс», «банда» тощо). Відповідно, якщо нам буде необхідно встановити обсяг поняття «група студентів фінансового факультету НУДПСУ», ми будемо рахувати не окремих студентів, а встановлювати кількість їхніх груп на відповідному факультеті.

Незбірними називають поняття, в обсязі яких узагальнюються окремі предмети («парта», «студент» тощо). Слід мати на увазі, що предмети складаються з частин, проте встановлюючи кількість предметів, ми абстрагуємося від цієї обставини і рахуємо не частини предметів, а самі ці предмети.

За типом елементів обсягу поняття поділяються на конкретні й абстрактні.

Конкретні — це поняття, в обсязі яких узагальнюються такі предмети (або такі упорядковані множини предметів), одиниці обсягу яких ми здатні сприйняти органами наших чуттів («парта», «чашка», «рослина» і т. ін.).

Абстрактні — це поняття, в обсязі яких узагальнюються властивості предметів, які самі по собі (поза предметами) не сприймаються органами чуттів людини («сила», «успішність», «розум» і т. ін.). Ми можемо побачити розумну або сильну людину, а не розум чи силу самі по собі.

За характером ознак поняття поділяють на позитивні і негативні, а також на співвідносні й неспіввідносні.

Говорячи про позитивність чи негативність понять, слід мати на увазі, що ці характеристики самим предметам чи явищам не належать. Ці характеристики розкривають ставлення суб’єктів пізнання до предметів чи явищ навколишньої дійсності. Один і той же предмет навіть в один і той же час може викликати у різних людей різне ставлення до себе. Хтось скаже, що цей предмет є хорошим, а хтось відмітить його негативні якості.

Позитивні поняття містять такі характеристики як «старанний», «гарний», «розумний» і т. ін. Приписуючи їх певним предметам, ми отримаємо поняття «старанний вчений», «гарний автомобіль», «розумний студент» тощо.

Негативні поняття розкривають погане ставлення суб’єктів до певних предметів чи явищ («потворний будинок» «жахливий день» та ін.), або вказують на відсутність у цих предметів позитивних характеристик («безвідповідальність», «нерозумність» і т. ін.).

Співвідносними називають поняття, зміст яких не має автономного смислу, тобто таке поняття стає осмисленим лише тоді, коли воно використовується разом з іншими поняттями у певному контексті, наприклад, «причина» (необхідно вказати, причина чого саме: наприклад, причина перемоги ФК «Шахтар» у кубку УЄФА в 2009 р. і т. ін.), «батьки» (треба вказати, чиї це батьки).

Неспіввідносними є поняття, зміст яких має автономний смисл («університет», «Чорне море» та ін.). Слід зазначити, що абсолютно неспіввідносних понять не існує. Адже, навіть наукові терміни, чий зміст є чітко визначеним, мають смислові відтінки, які розкривається лише у контексті їх використання. Більш того, навіть власні імена можуть набувати іншого значення. Наприклад, можна назвати іменем «Чорне море» кінотеатр, ресторан і т. ін. Відповідно, про неспіввідносність понять ми можемо говорити лише у тому чи іншому контексті.

 

 

Відношення між поняттями.

 

Поняття призначені всебічно відображати об’єктивний світ, в якому взаємозалежність і взаємозумовленість явищ мають універсальний характер. Відображаючи об’єктивний взаємозв’язок речей, поняття й самі вступають у різні відношення між собою. Ці відношення розрізняють за змістом і за обсягом.

За змістом поняття вступають у відношення непорівнюваності і порівнюваності.

Непорівнювані між собою поняття у своїх змістах не містять спільних ознак, наприклад, «право» і «атом». Але цей поділ має умовний характер, оскільки міра непорівнюваності буває різною. Вказані вище непорівнювані поняття можна об’єднати у таких філософських категоріях, як «матеріальне явище», «предмет дослідження науки» тощо. Справді, непорівнюваними між собою є найбільш загальні категорії філософії. Такі категорії часто розглядаються у парах: «матерія» і «свідомість» («ідея» і «дух»); «буття» і «небуття», «форма» і «зміст» тощо.

Змісти порівнюваних понять мають спільні ознаки, за якими вони порівнюються (звідси й їхня назва). Наприклад, поняття «мавпа» і «тигр» мають спільні ознаки: жива істота, ссавець, наявність лап і шкіри і т. ін. Порівнюючи між собою мавпу й тигра, ми починаємо краще розуміти їхню специфіку. Порівнювані поняття можуть бути сумісні або несумісні.

У відношенні сумісності перебувають поняття, ознаки яких допускають можливість повного (наприклад, «третій місяць року» і «місяць березень») або часткового (наприклад, «рослина» і «хижак») збігу їхніх обсягів. Інакше кажучи, це відношення існує між поняттями, що містять спільні елементи у своїх обсягах. Відношення сумісності понять має три підвиди: відношення рівнозначності (тотожності), підпорядкування (субординації) і перетину (часткового збігу).

У відношення рівнозначності перебувають поняття «X» і «У», обсяги яких повністю збігаються (наприклад, «X» — «сучасна гривня», «У» — «грошова одиниця сучасної України» або «амурський тигр» і «вид тигрів, що у дикій природі зустрічаються винятково на Далекому Сході Росії»). Змісти рівнозначних понять не співпадають, кожне з них відображає певний бік (властивість) одного й того ж самого предмета (або множини предметів). Зобразимо це відношення у вигляді наступної схеми:

 

Підпорядкування (субординація) це відношення між поняттями «X» і «У», в яких зміст першого (підпорядковуючого) становить частину змісту другого (підпорядкованого), а обсяг другого повністю входить в обсяг першого (наприклад: «X» (підпорядковуюче) — «злочин», «У» (підпорядковане) — «злочин проти майна»; «Х» - «будинок», «У» - «цегляний будинок» тощо). Подамо це відношення у вигляді схеми:

 

 

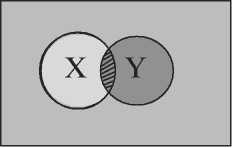
Два поняття «X», «У» знаходяться у відношенні перетину, якщо їхні змісти містять такі ознаки, які не виключають одна одну, але й не збігаються, тому їхні обсяги можуть часто (але не завжди) мати спільні елементи. Інакше кажучи, обсяги понять «X», «У» знаходяться у відношенні перетину, коли існують предмети, які мають лише ознаку «Х», одночасно існують предмети, які мають лише ознаку «У» і одночасно існують ще й предмети, які мають разом ознаки «Х» та «У» (наприклад, «X» — «автомобіліст», «У» — «вчений»; або «Х» - «цегляний будинок», «У» - «двоповерховий будинок» тощо). Подамо це відношення у вигляді схеми:

 

 

У відношенні несумісності перебувають поняття, в зміст яких входять ознаки, що виключають одна одну, тому їхні обсяги не можуть містити спільних елементів. Відношення несумісності понять має три підвиди: суперечливість (контрадикторність), протилежність (контрарність), співпідпорядкованість (координованість, одночасна підпорядкованість).

У відношенні суперечливості (контрадикторності) перебувають між собою поняття «X», «У», тоді, коли зміст одного з них просто заперечує зміст другого (наприклад, «X» — «річка» і «У» — «не річка»). Обсяг поняття «У» є доповненням до обсягу поняття «X». У такому разі «У» = «не X». В обсяг поняття «У» входять і обсяги понять: «будинок», «атом», «планета» і т. д. до нескінченності, адже і поняття «будинок» і поняття «планета» у своїх обсягах не місять спільних елементів із поняттям «річка». Для двох суперечливих між собою понять неможливо підшукати більш загальне (родове) поняття «Z», оскільки їх обсяги разом вони утворюють так зване універсальне поняття (обсяг якого охоплює собою множину всіх можливих предметів). Відобразимо це відношення у вигляді схеми:

 

 

У відношенні протилежності (контрарності) перебувають між собою поняття «X», «У», тоді, коли зміст одного з них не лише виключає ознаки другого, але й замінює іншими несумісними ознаками. Ці ознаки позначають протилежні між собою сторони або інші протилежні властивості. Протилежними між собою можуть бути лише дві ознаки (наприклад, «високий» - «низький», «більший» - «менший», «важчий» - «легший» і т. ін.) і, відповідно, - лише два поняття. (наприклад, «X» — «високий будинок», «У» — «низький будинок»). У протилежних понять завжди існує родове поняття «Z». У нашому прикладі таким поняттям є «будинок». Протилежні поняття не вичерпують обсяг родового поняття, адже, наприклад, окрім високих і низьких будинків, існують середні за висотою будинки. Часто виникає потреба в уточненні змісту таких понять. Наприклад, високими ми можемо вважати будинки, висота яких становить понад 50 метрів, низькими ті, висота яких буде до 10 метрів, відповідно, середніми будуть вважатися будинки, висота яких буде від 10 до 50 метрів. Відобразимо це відношення у вигляді схеми:

 

Співпідпорядкованими (координованими) є поняття «X», «У», які перебувають на одному рівні загальності й одночасно підпорядковані більш загальному (родовому для них) поняттю «2» (наприклад, «X» — «тигр», «У» — «вовк», «2» — «хижак»). Деякі ознаки понять не то­тожні, тому вони не містять у своєму обсязі спільних елементів. Співпідпорядкованими іншому поняттю можуть бути і два, і більше як два поняття. Відобразимо це відношення у вигляді схеми:

 

Судження – це форма мислення, в якій засобами природної чи штучної мови розкриваються зв’язки предметів із їхніми ознаками (в атрибутивних судженнях) або відношення між предметами (в релятивних судженнях).

Подібно до понять судження не можна плутати із мовними виразами, у яких їх висловлюють. Одне і те ж саме судження: «Я маю кусочок крейди» ми можемо висловити як «У мене є кусочок крейди» (укр.), «I have a piece of chalk» (англ.), «У меня есть кусочек мела» (рос.) і т. д.

Судження мають два види значень: змістовне і смислове.

Змістом судження (у логіці зміст часто називають матерією) є його істиннісне значення. У двозначній логіці висловлювань визнається існування лише таких істиннісних значень як «істина» і «хиба». В інших логічних системах може бути і більша кількість істиннісних значень. Наприклад, у трьохзначній логіці Я.Лукасевича додається значення «невизначено» («невідомо»). Третє значення може бути застосоване, наприклад, щодо оцінки суджень про майбутні події. Крім того, в сучасних багатозначних логічних системах використовуються такі змістовні значення як «правда – неправда», «точно – неточно» і т. ін. У межах даного курсу логіки, ми оперуємо лише двома значеннями істинності: «істина – хиба». Існує декілька гносеологічних теорій істини: кореспондентська, когерентська, іманентська, прагматична та ін. В більшості сучасних наукових теорій використовується кореспондентська теорія істини: «Аристотеля-Тарського». Згідно цій теорії істинним вважається таке судження, яке адекватно (вірно) позначає відповідну йому ситуацію у навколишній (позамовній) дійсності. Зрозуміло, якщо судження неадекватно (невірно) позначає відповідну йому ситуацію у навколишній (позамовній) дійсності, викривлює її, то таке судження оцінюється як хибне.

Наприклад, судження «У травні 31 день» буде істинним, а судження «Всі люди є студентами» буде хибним.

В кореспондентській теорії істини застосовується наступний метод: «А» є істинним тоді і лише тоді, коли А. Наприклад, судження: «Місто Черкаси є обласним центром України» є істинним тоді і лише тоді, коли місто Черкаси є обласним центром України. В першому випадку лапками ми позначили фрагмент мови (судження), а в другому випадку ми вже маємо фрагмент реальної (позамовної) дійсності.

Окрім змістовного (матеріального), судження мають смислове значення, тобто несуть певну інформацію про стан справ у навколишній (позамовній) дійсності. Ми можемо ототожнити два судження за їх матерією, але це не означає, що вони співпадуть за смислом. Наприклад, маємо два істинні судження: «Всі мавпи – живі істоти» і «Україна є європейською державою». Зрозуміло, що дані два судження передають зовсім відмінну інформацію. Матеріальне і смислове значення суджень досліджуються у логічній семантиці.

В більшості сучасних логічних систем термін «судження» не використовується, оскільки він є надто психологічним. Замість цього терміну використовується термін «висловлювання». Відповідно, в сучасній логіці є два основні структурні підрозділи: «логіка висловлювань» і «логіка предикатів». В першому підрозділі висловлювання розглядаються як цілісні («атомарні») структури, подальший логічний аналіз яких непотрібний. Відповідно, в логіці предикатів висловлювання розкладаються на менші структурні компоненти: суб’єкти, предикати, змінні, квантори, дескрипції і т. ін. В межах пропонованого курсу логіки ми будемо дотримуватися традиційного підходу до вивчення її предмету, тому замість терміну «висловлювання» будемо використовувати традиційний термін «судження».

 

Безпосередні умовиводи.

3. Опосередковані дедуктивні умовиводи із простих суджень:

а) логічна характеристика простого категоричного силогізму (ПКС);

б) складні, скорочені і складноскорочені силогізми побудовані із простих категоричних суджень: полісилогізми, ентимеми, епіхейреми, сорити;

в) умовиводи із простих релятивних суджень.

Безпосередні умовиводи.

Безпосередні умовиводи можна робити із простих і складних суджень. Із простих атрибутивних суджень безпосередні умовиводи робляться або завдяки логічним операціям (трансформації суджень), або через їх відношення (у «логічному квадраті»).

Безпосередні умовиводи через трансформацію суджень можна отримати завдяки операціям перетворення суджень або обернення суджень. Схеми таких умовиводів ми детально розглянули у темі «Судження як форма мислення», коли розглядали операції над судженнями, тому тепер обмежимось лише їхньою загальною характеристикою.

Загальне правило для таких умовиводів полягає в тому, що термін, не розподілений в засновку, не може бути розподіленим і у висновку.

Ми можемо отримати наступні умовиводи через обернення суджень:

1). Із загально-стверджувальних суджень-засновків ми можемо отримати або частково-стверджувальні судження-висновки (якщо у висхідних судженнях розподілений лише суб’єкт), або загально-стверджувальні судження-висновки (якщо у висхідних судженнях розподілені і суб’єкт, і предикат).

 

Наприклад:

1. Всі кримінальні злочини є правопорушеннями.

2. Деякі правопорушення є кримінальними злочинами.

 

Зрозуміло, що у першому судженні розподілений лише суб’єкт, тому отримали частково-стверджувальний висновок.

Із частково-стверджувальних суджень-засновків ми можемо отримати або частково-стверджувальні судження-висновки (якщо у висхідних судженнях не розподілені ні суб’єкт, ні предикат), або загально-стверджувальні судження-висновки (якщо у висхідних судженнях розподілений предикат).

Із загально-заперечних суджень-засновків ми можемо отримати лише загально-заперечні судження-висновки, оскільки у висхідних судженнях розподілені і суб’єкт, і предикат.

Із частково-заперечних суджень-засновків шляхом обернення ми не можемо отримати висновок, оскільки у висхідних судженнях не розподілений суб’єкт, отже він не може стати предикатом висновку.

Через операцію перетворення суджень ми можемо отримати наступні умовиводи:

Із загально-стверджувальних суджень-засновків отримаємо загально-заперечні судження-висновки.

Із загально-заперечних суджень-засновків отримаємо загально-стверджувальні судження-висновки.

Із частково-стверджувальних суджень-засновків отримаємо частково-заперечні судження-висновки.

Із частково-заперечних суджень-засновків отримаємо частково-стверджувальні судження-висновки.

У силогізмі за логічним квадратом зв’язок між засновком і висновком (представленими простими категоричними судженнями) відображають відношення контрадикторності, контрарності, субконтрарності і підкорення.

Детально ми розглянемо лише ті силогізми за логічним квадратом, які базуються на відношеннях контрадикторності (суперечності), оскільки саме вони набули найбільшого поширення у науці і практиці. Для решти відношень, ми обмежимось лише загальною характеристикою, тим більше, що їхні схеми ми вже розглядали у попередній темі.

Згадаємо, що за логічним квадратом у відношеннях контрадикторності перебувають судження виду: А-О; Е-І. Такі судження не можуть бути одночасно істинними і одночасно хибними.

Між А-О виникають наступні структури:

1. Якщо А, то не-О. Наприклад, якщо вірно, що всі фізики – вчені, то невірно, що деякі фізики не є вченими.

2. Якщо не-А, то О. Наприклад, якщо невірно, що всі люди є вченими, то вірно, що деякі люди не є вченими.

3. Якщо О, то не-А. Наприклад, якщо вірно, що деякі люди не є студентами, то невірно, що всі люди є студентами.

4. Якщо не-О, то А. Наприклад, якщо невірно, що деякі заочники не є студентами, то вірно, що всі заочники є студентами.

Між Е-І виникають наступні структури:

1. Якщо Е, то не-І. Наприклад, якщо вірно, що всі корови не є хижаками, то невірно, що існують деякі корови, які є хижаками.

2. Якщо не-Е, то І. Наприклад, якщо невірно, що всі люди не палять, то вірно, що деякі люди палять.

3. Якщо І, то не-Е. Наприклад, якщо вірно, що деякі ссавці є хижаками, то невірно, що всі ссавці не є хижаками.

4. Якщо не-І, то Е. Наприклад, якщо невірно, що деякі коти є собаками, то вірно, що жоден кіт не є собакою.

Враховуючи, що кожне судження: А, Е, І, О може перебувати у трьох типах відносин із іншими, відповідно, з кожного із них можна зробити по три висновки. Розглянемо такі типи відносин на прикладі загально-стверджувальних суджень (виду А):

Якщо А істинне (наприклад: всі шимпанзе – мавпи), то отримаємо наступні види суджень:

І істинне (наприклад: деякі шимпанзе – мавпи);

Е хибне (наприклад: всі шимпанзе – не мавпи);

О хибне (наприклад: всі шимпанзе – не мавпи).

Якщо А хибне (наприклад: всі шимпанзе – тигри), то отримаємо наступні види суджень:

І невизначене (може бути істинним або хибним) (у нашому прикладі І буде хибним: деякі шимпанзе – тигри);

Е невизначене (може бути істинним або хибним) (у нашому прикладі Е буде істинним: всі шимпанзе – не тигри);

О істинне (у нашому прикладі: деякі (мається на увазі, що, можливо, і всі) шимпанзе – не тигри).

Наведемо загальну схему всіх можливих відносин, що існують між судженнями: А, Е, І, О за логічним квадратом, користуючись якою, можна буде робити безпосередні умовиводи:

 

	А	Е	І	О
А і - х	-----	х - н	і – н	х – і
Е і - х	х – н	-----	х – і	і – н
І і – х	н – х	х– і	-----	н – і
О і - х	х – і	н - х	н – і	-----

 

Де і – істина;

х – хиба;

н – невизначено.

 

Безпосередні умовиводи можна робити також із простих релятивних суджень за допомогою логічних операцій обернення, перетворення або їхніх комбінацій. Оскільки ми розглянули їхні схеми у попередній темі, то тут ми їх розглядати не будемо. Зазначимо лише, що висновок у таких умовиводах випливає із загального характеру відношення R між суб’єктами х, у. Якщо, наприклад, встановлено, що х більше ніж у, то тим самим встановлено, що у менше ніж х.

 

Наприклад:

5>4

4<5

 

Якщо ж встановлено, що х – батько у, то тим самим встановлено, що у є сином х.

Ми можемо робити безпосередні умовиводи не лише із простих, але також й із складних суджень. Видів таких умовиводів існує необмежена кількість.

Існує загальне правило для таких умовиводів, - з одного складного судження можна вивести безпосередньо інше судження, якщо такі судження є еквівалентними (тобто, якщо їх поєднати за допомогою сполучника еквіваленції, то отримаємо завжди істинне судження). Іншими словами, поєднання таких судження (за допомогою сполучника еквіваленції) є логічними законами (вони є істинними лише завдяки своїй логічній формі). Основні схеми таких міркувань ми розглянули у попередній темі, коли розглядали трансформацію складних суджень.

 

Наприклад, ми можемо отримати наступний умовивід:

1. ~(АÙВ).

2. (~АÚ~В).

 

1. Неправда, що Дмитро працює юристом і, що Сергій працює економістом.

2. Неправда, що Дмитро працює юристом, або неправда, що Сергій працює економістом.

 

У вигляді складного судження наше міркування виглядало б так: ~(АÙВ)«(~АÚ~В). Читалося б воно так: якщо і тільки якщо неправда, що Дмитро працює юристом і що Сергій працює економістом, тоді неправда, що Дмитро працює юристом, або неправда, що Сергій працює економістом.

Недедуктивні умовиводи

а) повна і неповна індукція

Поняття «індукція» має два основних значення: по-перше, індукція — це метод пізнання, який полягає у переході знання від констатації тих або інших одиничних подій (фактів дійсності) до формулювання загальних припущень, що за подібних умов ці явища знову матимуть місце; по-друге, індукцією називають умовивід, в якому з одиничних суджень-засновків виводять часткове або загальне судження-висновок (тобто рух знань відбувається від менш загального знання до більш загального).

Вирізняють два основні види індукції: повну і неповну.

Повна індукція — це індуктивний умовивід, у якому на підставі знання, що певна ознака наявна у кожного окремого предмета даної множини, робиться висновок про наявність цієї ознаки у всіх предметів цієї множини.

Розглянемо формулу повної індукції:

1) S₁ є P

2) S₂ є P

...........................

n) S_n є P

S₁, S₂ … S_n (1£n<∞)

Всі S є Р.

N у цій формулі позначає кількість предметів множини. У формулі є вказівка на ту обставину, що множина має складатись із обмеженої кількості елементів (1£n<∞). в іншому разі ми не зможемо зробити висновок, що певну властивість має кожний об’єкт цієї множини. Наведемо приклад міркування, яке б відповідало вказаній формулі:

Перше вікно в аудиторії 276 ЦМЗ НУДПСУ має білу раму

Друге вікно в аудиторії 276 ЦМЗ НУДПСУ має білу раму

………………………………………………………….

П’яте вікно в аудиторії 276 ЦМЗ НУДПСУ має білу раму

Кількість вікон в аудиторії 276 ЦМЗ НУДПСУ обмежена і дорівнює 5

Усі вікна в аудиторії 276 ЦМЗ НУДПСУ мають білі рами.

Повна індукція є правильним із логічного погляду міркуванням, відповідно, за умови наявності лише істинних засновків, ми завжди отримаємо істинний висновок.

Неповна індукція — це індуктивний умовивід, в якому висновок про наявність певної властивості у всього класу (множини) предметів робиться на підставі знання про наявність цієї властивості лише у деяких предметів цього класу. Кількість предметів множини, як правило, полишається невідомою. На відміну від повної індукції, неповна не гарантує отримання істинного висновку за умови наявності істинних засновків, отже, вона не є логічно правильним умовиводом. Відповідно, висновок неповної індукції є ймовірнісним, тобто він може бути як істинним, так і хибним. Розглянемо формулу таких міркувань:

1) S₁ є P

2) S₂ є P

.........................

m) S_m є Р

S₁, S₂… S_m... S_n (1£m<n)

Всі S є Р

Наведемо приклад міркування, яке б відповідало наведеній схемі. Перед тим, як розглянути приклад, уявимо собі наступну ситуацію. На митницю поступила інформація, що певна вантажівка, яка перевозить розчинну каву (10 000 банок), окрім цього задекларованого вантажу, перевозить заборонені речовини (наприклад, наркотики). Митники можуть зробити повну або часткову перевірку цього вантажу. Якщо вони зроблять повну перевірку і не знайдуть забороненого вантажу, то їхній висновок, що вантаж є чистим буде зроблено за формулою повної індукції. Якщо вони перевірять не 10 000 банок, а менше (хоча б, навіть на одну банку) і зроблять цей же висновок, то їх міркування відповідатиме схемі неповної індукції.

1) Перша банка містить лише розчинну каву

2) Друга банка містить лише розчинну каву

…………………………………………………

100) Сота банка містить лише розчинну каву

Перша, друга... сота банка містять розчинну каву, але є й інші (9 900), які ми не перевіряли

Усі банки містять лише розчинну каву (ймовірно, що висновок істинний).

Ми припустили, що висновок неповної індукції є істинним, але існує ймовірність, що деякі банки можуть містити заборонені речовини. У такому разі виявиться, що висновок умовиводу був хибним. Для того, щоб остаточно визначитися у цьому питанні, необхідно було б перевірити усі банки. Але така перевірка забрала б багато часу, що може виявитися недоцільним. Неповна індукція не претендує на встановлення остаточної істини. її цінність полягає зовсім в іншому: вона є невичерпним джерелом гіпотез про навколишню дійсність. Існують певні математичні закономірності для неповної індукції. Якщо відома кількість предметів у множині, то можна вираху