
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение доходности и риска при формировании портфеля ценных бумаг.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Портфель - это набор финансовых активов, которыми располагает инвестор. Ожидаемая доходность портфеля определяется как средневзвешенная ожидаемая доходность входящих в него бумаг, то есть:
где E(r p) - ожидаемая доходность портфеля за определенный период1; E(r 1), E(r 2); E(r n) - ожидаемая доходность соответственно первой, второй и п-й бумаги; она рассчитывается как средняя арифметическая доходности бумаги за предыдущие периоды времени; Ɵ1\Ɵ2\Ɵп - удельный вес в портфеле первой, второй и п- й бумаги.
Удельный вес актива в портфеле определяется как отношение её стоимости к стоимости всего портфеля:При этом сумма всех удельных весов, входящих в портфель активов равна единице.
где Ɵi- удельный вес i-го актива; Рi- стоимость i-го актива; Рр- стоимость портфеля. Ожидаемый риск портфеля Марковиц. определил риск при помощи хорошо известной статистической величины - вариации как меры возможных отклонений от ожидаемого (среднего) значения. Использование вариации для измерения риска
вариация учитывает не только размер отклонений возможных значений доходности от среднего, но и вероятность такого отклонения.дисперсия указывает меру неопределенности в ожиданиях инвестора, который оценивает будущую доходность как среднюю по всем возможным значениям. Стандартное отклонение. Поскольку вариация имеет размерность квадрата измеряемой величины, ее принято преобразовывать в стандартное отклонение, т.е. извлекать квадратный корень. Тогда риск (о) получает ту же размерность, что и доходность:
Риск тем больше, чем больше вариация (var) или стандартное отклонение(σ). Ковариация и корреляция. Ковариация демонстрирует степень зависимости двух случайных величин.
Ковариация может принимать положительные, отрицательные значения и равняться нулю.
18.5 где covxy - ковариация доходности активов X и Y. Связь между ковариацией и корреляцией.
где сorrxу - коэффициент корреляции переменных X и Y; σх - стандартное отклонение переменной X; σy- стандартное отклонение переменной Y.
18.12 Отсюда очевидно, что портфель активов с некоррелируемыми доходностями способен снизить риск.
Выводы для портфеля из двух активов. • если портфель состоит из активов с корреляцией +1, то возможно лишь усреднить, но не уменьшить совокупный риск; • если портфель состоит из активов с корреляцией меньше +1, его риск уменьшается по мере уменьшения корреляции доходностей активов, при этом сохраняется неизменный уровня ожидаемой доходности портфеля; • если портфель состоит из активов с корреляцией -1, можно сформировать портфель без риска; • при формировании портфеля следует подбирать активы с минимально возможной корреляцией.
18.13
где σ2р - риск портфеля; Ɵi - удельный вес i-roактива в портфеле; Ɵj- удельный вес j-roактива в портфеле; covij- ковариация доходностей i-roи j-roактивов.
Знак двойной суммы означает, что, раскрывая формулу 18.13, сначала следует взять значение i=1 и умножить на него все значения j от 1 до п. Затем повторить данную операцию, но уже для i=2, и т.д. В итоге получим п 2 слагаемых:
Доминирующий портфель. Портфель (актив) имеющий более высокий уровень доходности при том же уровне риска или более низкий риск при той же ожидаемой доходности, чем остальные портфели (активы), называется доминирующим. 70. Показатели эффективности управления портфелем ценных бумаг.
Трудно получить однозначный вывод, если сравнивать портфели лишь только на основе их абсолютных значений. Например, доходность одного портфеля составила 60%, а второго 70%. На первый взгляд, вывод однозначен: управление второго менеджера оказалось более предпочтительным. Но так ли это, если знать, что второй менеджер шёл на риски, в два раза превышающие риски первого менеджера? Ответ может быть только отрицательным. Поэтому для оценки эффективности управления портфелем используются относительные показатели, учитывающие не только доходность, но и риск портфеля. С 1960-е годов для акций наиболее распространенными в этой области были три показателя, или индекса: индекс Трейнора, индекс Шарпа и индекс Дженсена. Для облигаций предусмотрены особые индексы. Сначала рассмотрим индекс для облигаций Индекс для облигаций. В качестве меры риска в нем учитывается относительная дюрация: Коэффициент эффективности портфеля облигаций (rp-rf)/(Dp/Dm) где Dp/'Dm- отношение дюрации портфеля облигаций к дюрации рыночного портфеля облигаций. Для акций набор индексов более разнообразен. Индекс Трейнора представляет меру полученной избыточной доходности на единицу риска. При этом избыточный доход определяется как разность между доходностью портфеля и безрисковой ставкой доходности за рассматриваемый период. Мерой риска в данном индексе является «бета» портфеля:
где rp- доходность портфеля за рассматриваемый период; rf- ставка без риска за данный период. Индекс Шарпа, как и индекс Трейнора, является мерой соотношения доходность/риск. В числители этого индекса находятся те же величины, что и в индексе Трейнора. В качестве же меры риска используется стандартное отклонение:
Индексы Шарпа и Трейнора приводят к получению примерно одинаковых рейтингов, если инвестор имеет дело с хорошо диверсифицированными портфелями. В противном случае индексы могут существенно друг от друга отличаться. Индекс Шарпа при измерении риска учитывает стандартное отклонение. В связи с этим его следует использовать при оценке портфеля с малой диверсификацией. Индекс Трейнора лучше использовать при оценке широко диверсифицированного портфеля. При определении эффективности управления портфелем, инвестор должен произвести два сопоставления: найти наилучший портфель среди данного множества, сравнить активный портфель с результатами рынка Индекс Дженсена (JensenIndex). При построении индекса Дженсена используется модель определения цен фиксированных активов (САРМ). С её помощью определяется, получил ли инвестиционный менеджер более высокие или низкие по сравнению с выбранным рыночным индексом результаты. «Эмпирическим» аналогом САРМ является уравнение:
где е - случайная ошибка модели.
На словах это выражение толкуется так: Избыточная доходность = «Бета» * Избыточная доходность относительно индекса рынка + Случайная ошибка. Если полученная менеджером избыточная доходность не превосходит ту, которая получается по данной формуле, то это значит, что «добавленной стоимости» получено не было. И вот здесь, чтобы определить степень отклонения полученного результата от эталонного, описываемого «бетой», Дженсен ввел в уравнение дополнительный фактор. Коэффициент «альфа» служит мерой эффективности управления портфелем данным менеджером.
Здесь свободный член «альфа» (ар) выражает часть доходности, которая была получена исключительно за счёт действий инвестиционного менеджера, то есть: Избыточная доходность = Доходность от действий менеджера + «Бета» * Избыточная доходность относительно индекса рынка + Случайная ошибка. Менеджер пассивной стратегии не стремится получить доходность выше рыночной; тем самым он ориентируется на результаты, которые находятся на ожидаемой линии SML. Если при этом фактическая альфа не равна нулю, то менеджер недостаточно точно спрогнозировал будущую рыночную конъюнктуру. Как известно, CARM является моделью одного временного периода с одним значением гfи Е(rт). Если же рассматривать продолжительный период Т, состоящий из нескольких отрезков времени ti, то для каждого периода будет меняться и конъюнктура. То есть для каждого временного периода пассивный менеджер должен строить свою линию SML с собственными значениями rfи E(rm). На базе значений rfи E(rm) для каждого отрезка времени ti можно рассчитать ожидаемую SML для периода Т, на основе средних значений за период Т.
Тем самым ар, полученная как отклонение реальной доходности портфеля от его предполагаемой доходности, отразит способность пассивного менеджера предвидеть будущую конъюнктуру. Для активного менеджера положительная альфа в рамках периода t (в рамках одного периода при неизменной конъюнктуре) свидетельствует о его способности обнаружить недооцененные ценные бумаги. Для длительного периода Т (множество периодов t) положительная альфа может быть как результатом адекватного выбора активов, так и времени сделок с ними. Для облигаций коэффициент альфа определяется на основе линии SML для облигаций с использованием относительной дюрации в качестве значения беты. Как и индекс Тейнора, индекс Дженсена строится на предположении о полной диверсификации портфеля, при которой с портфелем связан только систематический риск. Статическая оценка коэффициента «альфа» довольно чувствительная к изменению «бета» портфеля. Чтобы избавиться от этой зависимости, коэффициент «альфа» можно разделить на ожидаемую доходность портфеля, что позволит отразить систематический риск.
[1] выписка предоставляется только при наличии операций по счету, а также по просьбе клиента (но это уже может быть платная услуга), в обязательном порядке выписка формируется по состоянию на 1 января, и остаток сверяется с данными бухгалтерского учета клиента.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 927; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.213.208 (0.009 с.) |

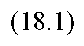


 Компактно формула (18.1) записывается следующим образом:
Компактно формула (18.1) записывается следующим образом:

 Вариация, или дисперсия, случайной величины служит мерой разброса её значений вокруг среднего значения. Для доходности (как случайной величины) вариация, оценивающая «степень отклонения» возможных конкретных значений от средней или ожидаемой доходности, служит мерой риска, связанного с данной доходностью. Формула для определения вариации доходности актива записывается следующим образом:
Вариация, или дисперсия, случайной величины служит мерой разброса её значений вокруг среднего значения. Для доходности (как случайной величины) вариация, оценивающая «степень отклонения» возможных конкретных значений от средней или ожидаемой доходности, служит мерой риска, связанного с данной доходностью. Формула для определения вариации доходности актива записывается следующим образом:
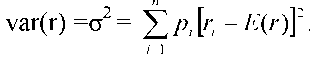

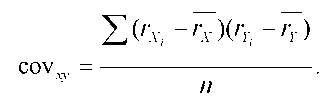

 Риск портфеля двух активов с некоррелируемыми доходностями. В случае отсутствия корреляции между доходностями активов формула принимает вид:
Риск портфеля двух активов с некоррелируемыми доходностями. В случае отсутствия корреляции между доходностями активов формула принимает вид: Как известно, можно получит портфель с минимальным риском при отсутствии корреляции доходностей двух активов. Для этого следует продифференцировать уравнение 18.12 поƟxи приравнять его к нулю при том, что Ɵ у = 1 –Ɵx:
Как известно, можно получит портфель с минимальным риском при отсутствии корреляции доходностей двух активов. Для этого следует продифференцировать уравнение 18.12 поƟxи приравнять его к нулю при том, что Ɵ у = 1 –Ɵx: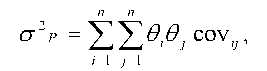 Риск портфеля из нескольких активов. Теперь выясним, как определяется риск портфеля, состоящего из нескольких активов. Он рассчитывается по формуле:
Риск портфеля из нескольких активов. Теперь выясним, как определяется риск портфеля, состоящего из нескольких активов. Он рассчитывается по формуле:



 Используя заданные в форме временных рядов данные по доходности портфеля и рыночного индекса, получим систему уравнений регрессии:
Используя заданные в форме временных рядов данные по доходности портфеля и рыночного индекса, получим систему уравнений регрессии:



