
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Допустимость риска в управлении портфелем ценных бумаг.Содержание книги
Похожие статьи вашей тематики
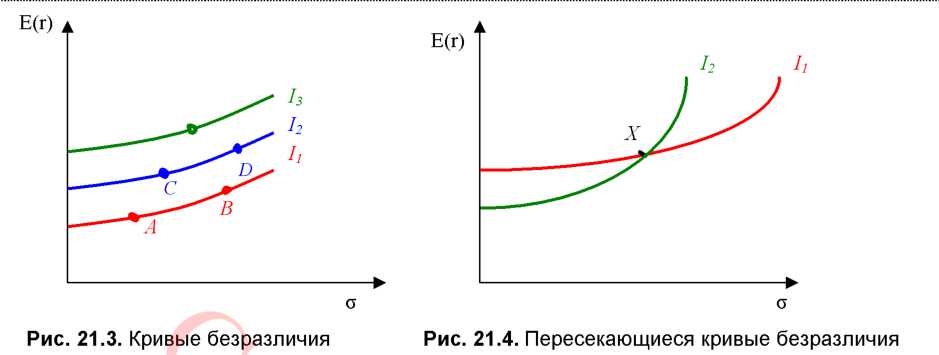
Поиск на нашем сайте Рациональный инвестор стремится получить от своих действий максимум полезности, то есть максимум ожидаемой доходности при минимальном риске. Метод, который будет применён для выбора наиболее желаемого портфеля, использует так называемые кривые безразличия. Эти кривые отражают отношения инвестора к риску и доходности и, таким образом, могут быть представлены в виде графика, где по горизонтальной оси откладывается риск, мерой которого стандартное отклонение, а по вертикальной оси - вознаграждение, мерой которого является ожидаемая доходность. На рис. 21.3 изображены кривые безразличия инвестора. Каждая кривая представляет все комбинации портфелей, которые обеспечивают заданный уровень предпочтений инвестора. кривые безразличия не могут пересекаться (рис. 21.4.).
Любой портфель, лежащий на кривой безразличия, которая находится выше и левее, более привлекательна, чем любой портфель, лежащий на кривой безразличия, которая находится ниже и правее.каждый инвестор имеет бесконечное число кривых безразличия. Избегание риска. В качестве общего допущения следует исходить из того, что каждый инвестор стремится избегать риска, то есть выбирает портфель с меньшим стандартным отклонением.различные инвесторы имеют различные графики кривых безразличия, инвестор с высокой степенью избегания риска имеет кривые безразличия с более крутым положительным наклоном. У инвестора, абсолютно безразличного к риску, эти линии расположены горизонтально, а у азартного инвестора обладают отрицательным наклоном. Коэффициент неприятия риска демонстрирует наклон кривой безразличия к оси абсцисс, т.е. измеряет риск в единицах ожидаемой доходности. Коэффициент показывает, сколько единиц ожидаемой доходности приходится на единицу риска. Чем больше величина Rа, тем менее расположен к риску инвестор и тем большего вознаграждения потребует он при увеличения риска. Коэффициент неприятия риска имеет вид:
Величина, обратная Rа, называется коэффициентом допустимости риска - Rt. сколько единиц риска готов допустить инвестор при возрастании ожидаемой доходности на одну единицу (сколько единиц риска приходится на единицу ожидаемой доходности):
С увеличением RТ сокращается вознаграждение в единицах ожидаемой доходности, на которое претендует инвестор, т.е. такой инвестор более склонен к риску. Заменим в формуле 21.4 Ra на RТ.
где Ɵа- удельный вес портфеля акций в формируемом портфеле; Ɵ0 - удельный вес портфеля облигаций в портфеле; σ 2а - дисперсия доходности портфеля акций; σ 2о ~ дисперсия доходности портфеля облигаций; covao- ковариация доходностей портфелей акций и облигаций.
21.11 При этом в своей деятельности инвестор, принимая инвестиционное решение, должен минимизировать вероятность того, что доходность его портфеля окажется ниже поставленной цели.
Если исходить из того, что доходность портфеля подчиняется нормальному распределению1, то управляющий портфелем должен сформировать портфель так, чтобы между его ожидаемой доходностью и доходностью по взятым обязательствам перед клиентом, располагалось максимально возможное значение стандартных отклонений (</) доходности портфеля, т.е. следует максимизировать величину d:
где r - уровень доходности по обязательствам управляющего портфелем.
Формула 21.14 является функцией полезности инвестора, пересекающая ось ординат в точке r(рис. 21.7). В результате получен веер функций полезности, проходящих через точку r. При этом более высоко расположенная функция приносит большую полезность. Оптимальный портфель расположен в точке В.производным инструментам (о чём речь пойдёт в параграфе 21.3), по которым можно достичь нулевой ошибки слежения.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 752; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |


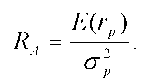
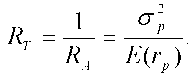
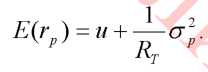 21.6
21.6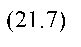
 Инвестор должен найти доступную наиболее высоко расположенную кривую безразличия, то есть найти значение и, принадлежащее кривой безразличия и касательную к эффективной границе. Доходность в точке и называется гарантированная эквивалентная доходность:
Инвестор должен найти доступную наиболее высоко расположенную кривую безразличия, то есть найти значение и, принадлежащее кривой безразличия и касательную к эффективной границе. Доходность в точке и называется гарантированная эквивалентная доходность: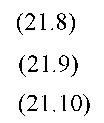
 Величину и следует максимизировать. Для этого нужно определить, какое количество различных активов следует включить в портфель при данном значении Rt. Тогда инвестор должен максимизировать и в случае если:
Величину и следует максимизировать. Для этого нужно определить, какое количество различных активов следует включить в портфель при данном значении Rt. Тогда инвестор должен максимизировать и в случае если: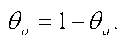 На основании формулы 21.10 выразим удельный вес формулы облигаций:
На основании формулы 21.10 выразим удельный вес формулы облигаций:
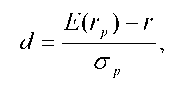 21.13
21.13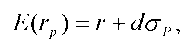
 Запишем выражение 21.13 в следующем виде:
Запишем выражение 21.13 в следующем виде:


