
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эффективный набор портфелей ценных бумаг.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Правила построения границы эффективных портфелей Марковица позволяют находить оптимальный портфель для любого количества ценных бумаг. Однако для определения весов каждого актива необходимо выполнять большой объем вычислений. В самом деле, если портфель объединяет n активов, то для построения границы эффективных портфелей необходимо предварительно вычислить n значений ожидаемых (средних арифметических) доходностей Е(ri) каждого актива, n величин дельта2 дисперсий всех доходностей и п(п — 1) / 2 выражений ковариаций дельта. активов в портфеле.
При увеличении числа активов в портфеле количество необходимых ковариаций становится непомерно большим. Например, если инвестор желает сформировать портфель из 30 акций, ему необходимо вычислить 435 ковариаций, 30 ожидаемых и 30 дисперсий, т.е. около 500 величин. При 100 активов в портфеле необходимое количество исходных данных превысит 5000. В 1963 г. Уильям Шарп предложил новый метод построения эффективных портфелей, позволяющий существенно сократить объемы необходимых вычислений. В дальнейшем этот метод модифицировался и в настоящее время известен как одноиндексная модель. Шарпа.
В основе модели лежит метод линейного регрессионного анализа, позволяющий связать две случайные зависимые переменные величины X и Y линейным выражением типа:
Переменной X считается величина какого-то рыночного показателя: темпы валового внутреннего продукта, уровень инфляции, индекс цен потребительских товаров и т.п. Сам Шарп в качестве такой переменной рассматривал доходность рыночного портфеля rm,вычисленную на основе индекса S&P500. В российских условиях, естественно, можно использовать данные отечественных индексов: РТС или ММВБ.Уравнение модели может иметь, например, следующий вид:
где E(rj) - ожидаемая доходность актива; у, - доходность актива в отсутствии влияния на него рыночных факторов; Bi- коэффициент бета актива; Е(rт) - ожидаемая доходность рыночного портфеля; £, - независимая случайная ошибка, свидетельствующая о том, что значения Е(ri) и Е(rт)
отклоняются от линейной зависимости 20.16. Она показывает специфический риск актива, который нельзя объяснить действием рыночных сил.
где Е(rр) - ожидаемая доходность портфеля; BР - бета портфеля; ур - доходность портфеля в отсутствии влияния рыночных факторов. В графическом виде данная модель изображена на рис. 20.14. Она демонстрирует зависимость между доходностью рынка (rт) и доходностью актива (ri) и представляет собой прямую, которая получила наименование линией характеристики или характеристической линии.
Доходность рынка здесь - независимая переменная. Наклон линии характеристики определяется коэффициентом бета, а пересечение с осью ординат - значением показателяyi. Бета определяется по формуле:
yi- находится по формуле
где ri - средняя доходность i-го актива за предыдущие периоды времени; rm - средняя доходность рынка за предыдущие периоды времени.
На данном рисунке бета положительна, поэтому наклон линии характеристики соответственно положительный: при увеличении доходности рынка доходность актива повышается, а при понижении - падает. Однако, как уже было изображено на рис. 20.5, наклон рынка теоретически может быть любым. А если построить график модели для самого рыночного портфеля относительно рыночного портфеля, то значение у него равно нулю, а беты, соответственно, +1
Набор эффективных портфелей Одно из главных достоинств модели Шарпа состоит в том, что она позволяет значительно сократить объёмы вычислений при определении оптимального портфеля, давая при этом результаты, близко совпадающие с получаемыми по модели Марковица. Это достигается на основе ряда преобразовании. Ковариация i-го и j -го активов на основе уравнения Шарапа равна:
Экономичность модели Шарпа можно проиллюстрировать на таком примере: при формировании портфеля из 30 активов для определения границы эффективных портфелей потребуется 3 • 30 + 2 = 92 исходных данных по модели Шарпа и 495 (то есть, в 5 раз больше) по модели Марковица. Однако при использовании формулы 20.20 следует помнить, что экономия в вычислениях происходит за счет уменьшения точности оценки.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 474; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.143.118 (0.007 с.) |



 Если уравнение 20.16 применить к широко диверсифицированному портфелю, то значения случайных переменных е,, погасят друг друга и ими можно пренебречь. То есть, модель Шарпа принимает вид:
Если уравнение 20.16 применить к широко диверсифицированному портфелю, то значения случайных переменных е,, погасят друг друга и ими можно пренебречь. То есть, модель Шарпа принимает вид:
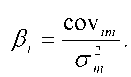





 Для определения риска портфеля подставим формулу 20.19 в формулу, предложенную Марковитцем:
Для определения риска портфеля подставим формулу 20.19 в формулу, предложенную Марковитцем:



