
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плоское напряженное состояниеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В общем случае при переходе из одной точки в другую главные напряжения изменяются непрерывно по величине и направлению. Случай, когда одно из главных напряжений становится равным нулю, называют плоским (двухосным) напряженным состоянием в точке. В соседних точках тела напряженное состояние может быть пространственным (трехосным). Встречаются и такие случаи, когда во всех точках тела напряженное состояние плоское и при этом площадки с нулевым главным напряжением параллельны друг другу. В таком случае все тело испытывает плоское напряженное состояние. Примером может служить пластинка, подверженная воздействию поверхностной и (или) объемной нагрузки, распределенной равномерно по толщине. При этом равны нулю главные напряжения на площадках в плоскости пластинки, а два других отличны от нуля и, вообще говоря, изменяются при переходе из одной точки в другую. Три независимые скалярные величины, соответствующие составляющим напряжений, определяют тензор напряжений:
Для определения главных напряжений представляет интерес исследование напряжений, действующих лишь на площадках, перпендикулярных к главной площадке с нулевым главным напряжением. Рассмотрим прямую призму с основанием ВС D высотой dz (рис.4.2). Уравнения равновесия запишем в виде проекции сил на направления σ α и τ α: σ α dzds – (σ y dzds cosα) cosα– (τ dzds cosα)sinα –– (σ x dzds sinα) sinα – (τ dzds sinα) cosα = 0, τ α dzds + (σ y dzds cosα) sinα – (τ dzds cosα) cosα –– (σ x dzds sinα) cosα + (τ dzds sinα) sinα= 0. После сокращения на dzds и преобразо-вания получим σ α = σ x sin2α + σ y cos2α+τsin2α; τ α = Чтобы определить положение главных площадок, следует либо приравнять нулю производную d σ α/ d α, либо положить равными нулю касательные напряжения τ α ввиду их отсутствия на главных площадках. В обоих случаях получаем следующее уравнение для угла наклона главных площадок (α0):
откуда tg2α0= 2τ /(σу– σх), чему соответствуют углы α0′ и α0′+ 90°, которые определяют две взаимно перпендикулярные площадки. Исследуя вторую производную d 2 σ α/ d α2, можно убедиться, что на главной площадке под углом α0′ при σ y >σ x действует максимальное главное напряжение σ1,а на площадке под углом α0′+ 90° действует минимальное главное напряжение σ2. Для определения главных (экстремальных нормальных) напряжений отразим значение угла α0 в выражении σ α, используя при этом формулы для sin2α0, соs2α0, соs2α0, sin2α0, приведенные в п.3.4. В итоге
Если одно из напряжений σ x или σ y равно нулю, то формула примет вид
Экстремальные касательные напряжения можно выразить через главные напряжения: ±
Они действуют на площадках, наклоненных к главным под углом 45° и направлены от σmin к σmax (рис.4.3). В общем случае на этих площадках σ α ≠ 0. Если оси х и у совмещены с главными осями 1 и 2, то σ α = σ1sin2α + σ2cos2α; τα=
В случае σ1 = σ2 = σ на всех площадках, проходящих через исследуемую точку, τ α = 0, σ α = σ. Такое напряженное состояние называется равномерным двухосным растяжением (или сжатием). Рис. 4.3 При одноосном напряженном состоянии (σ2 = σ3 = 0) имеем σ α = σ1sin2α; τ α = Экстремальные касательные напряжения равны ± σ1 /2. 4.3. Перемещения и деформации Твердое тело, как правило, закреплено. В таком случае перемещение точки тела вызывается только его деформированием. Это перемещение характеризуется вектором Элементарный параллелепипед, вырезанный в окрестности какой-либо точки, деформируется таким образом, что изменяется длина его ребер и искажаются первоначально прямые углы между гранями, т.е. изменяются объем и форма.
угловое перемещение (угол поворота) ∆α малым по сравнению с единицей, так что cos∆α ≈ 1. Величина ∆λ = ∆ l ' – ∆ l представляет собой абсолютное изменение первоначальной длины отрезка АВ. Величина ∆λ/∆ l есть средняя линейная деформация вдоль оси n в точке А. Уменьшая размеры отрезка, в пределе получаем
Безразмерная величина ε n есть истинная линейная деформация вдоль оси n в точке А. Полагая, что λ − непрерывная функция l, получим
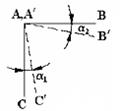
ε n = ∂ λ /∂ l. Если λ зависит от одной переменной l, то ε n = d λ / dl. Для определения деформации сдвига в точке А в плоскости mn возьмем на этой плоскости два малых отрезка АВ и АС, пересекающихся в точке А под углом 90°. После деформирования тела они обратятся в отрезки А'В' и А'С' с иным углом пересечения и расположатся в другой плоскости m ' n ', составляющей с первоначальной угол ∆α. Принимая, как и раньше, cos∆α ≈ 1, определим деформацию сдвига как разность величин углов В'А'С' и ВАС. Наложим угол В'А'С' на угол ВАС (рис.4.5) и установим углы поворота отрезков относительно своих первоначальных положений – α1 и α2. Величина α1 + α2 = γ mn и есть деформация сдвига в точке А в плоскости mn.
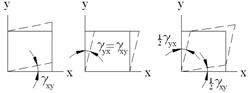
Полагая деформации малыми, мы можем в дальнейшем пренебрегать ими по сравнению с едини-цей, а также их высокими степенями по сравнению с первой степенью. Рис. 4.5 Деформированное состояние в точке – состояние тела в окрестности данной точки, определяемое совокупностью деформаций всех линейных элементов, проходящих через данную точку. В случае малых деформаций оно полностью определяется линейными деформациями трех взаимно перпендикулярных линейных элементов тела, проходящих через данную точку, и тремя деформациями сдвига этих линейных элементов. Соответствующие шесть независимых скалярных величин определяют тензор деформаций:
Здесь   (при γ yx =γ xy),…Последнее оправдывается идентичностью трех ситуаций для грани деформированного параллелепипе-да, что видно, например, из рис. 4.6 (в плоскости xy). (при γ yx =γ xy),…Последнее оправдывается идентичностью трех ситуаций для грани деформированного параллелепипе-да, что видно, например, из рис. 4.6 (в плоскости xy).
Рис. 4.6
Главные оси деформации – три взаимно перпендикулярные прямые, прохо-дящие через данную точку тела и совпадающие по направлениям с такими тре-мялинейными элементами тела, которые остаются взаимно перпендикулярны-ми и после деформации. Линейные деформации по направлениям этих осей на- зываются главными деформациями и обозначаются ε1, ε2, ε3 (ε1 ≥ ε2 ≥ ε3). Кинематические граничные условия на части поверхности тела с заданным вектором перемещений
4.4 Практикум Примеры 1. По двум взаимно перпендикулярным площадкам действуют только касатель-ные напряжения τ (чистый сдвиг). Определить положение главных площадок и величины главных напряжений.
Поскольку между главными напряжениями существует соотношение σ1 σ1>τ; σ2>τ; σ3>-τ; tg2αо= Повернув, на αо= - 45
Решение. Следует помнить, что в формулах: σгл.= 1) σα > σβ алгебраически, 2) Знак τα определяется на площадке, где действует большее нормальное напряжение (σα), а учитывая, что Q= если поперечные силы Q > 0, т.е. стремятся повернуть площадку “по часовой стрелке”,
3) если αо > 0, то поворот совершают “против часовой стрелки” от вектора σα > 0, с учётом сказанного: σα= + 60 МПа; σβ= -140 МПа; τα= - 40 МПа. σгл.= σ1= + 67.7 МПа; σ2=0; σ3= -147.7 МПа (касательные напряжения в главных площадках отсутствуют). tg2αо= αо =10.6 (поворот против часовой стрелки).
Вопросы для повторения
1.Дайте определение понятия «напряжение». Какие виды напряжения различают? 2.Что называют касательным и нормальным напряжением? 3.Какова размерность напряжений? 4.Что обозначают индексы касательного напряжения? 5.Какова зависимость между полным, нормальным и касательным напряжением в точке данного сечения? 6.Как связаны напряжение и внутренние силовые факторы? 7.Какие виды деформаций связаны с каждым из внутренних силовых фак-торов? 8.Чем характеризуют напряженное состояние в точке? 9.Как формулируется закон парности касательных напряжений? 10. Какие площадки называют главными? 11.Чему равны касательные напряжения на главных площадках? 12.Как обозначают главные напряжения? Каково между ними соотноше-ние? 13.Как изменяются величины 14.Дайте определение линейного, плоского, объемного напряженного сос-тояний используя понятия «главные площадки». 15.Как определить экстремальную величину касательных напряжений, зная напряжения σх, σу, τ в случае плоского напряженного состояния? 16.Как ориентированы площадки, в которых действуют τэкстр, по отноше-нию к главным? 17.Какие деформации называют линейными и какие угловыми?
Тесты для повторения 1. Как изменится угол αо, если горизонтальная компонента нормального напря-жения изменит направление на противоположное (при условии, что σх >σу)?
(б) возрастёт, но сохранит знак; (в) уменьшится и изменит знак; (г) возрастёт и изменит знак. Ответ: (а), поскольку в первом случае tg2 αо= 2. Для случая линейного напряжённого состояния (частный случай объёмного, когда два главных напряжения равны нулю) число главных площадок равно: (а) 1; (б) 2; (в) 3; (г) бесконечное множество. Ответ: (г), поскольку площадка, перпендикулярная действующему главному напряжению определена в пространстве, а две взаимно перпендикулярны пер-вой и одновременно перпендикулярны между собой, то они могут иметь беско-нечное число положений.
3. Как изменится сумма нормальных напряжений на любых двух взаимно пер-пендикулярных площадках при плоском напряжённом состоянии, если площад-ки повернуть по часовой стрелке относительно главных?
(а) возрастёт; (б) не изменится; (в) уменьшится; (г) станет равным нулю.
Ответ: (б), поскольку сумма нормальных напряжений в двух взаимно перпен- дикулярных площадках равна сумме главных напряжений, то для любой пары взаимно перпендикулярных площадок это сохраняется.
4. Для случая чистого сдвига наименьшее из трёх главных напряжений равно: (а) σ3 = τ; (б) σ3 = 0; (в) σ3 = -τ; (г) σ3 = σ1. Ответ: (в), так как в главных площадках при плоском напряжённом состоянии σгл= ± τ, т.е. σ3 равно наименьшему значению (алгебраически). 5. Чему равны экстремальные значения касательных напряжений, если извест-но, что одно главное растягивающее напряжение равно 40 МПа, а второе, сжи-мающее равно 60 МПа?
(а) 50 МПа (б) -10 МПа; (в) 40 МПа; (г) –20 МПа. Ответ: (а), поскольку установлено, что τα= Контрольные тесты
(а) ΜZ=; (б) MY=; (в) QY=; (г) QZ =. (д) =
2. Сколько независимых скалярных величин, соответствующих составляю-щим напряжений по трем взаимно ортогональным площадкам определяют тен-зор напряжений? (а) 4; (б) 6; (в) 9; (г) 12.
3. По какой из приведенных формул определяют главные напряжения при плоском напряженном состоянии? (а)σx·sin2α+σy·cos2α+τsin2α; (б) (в) 4. По какой из приведенных формул определяют величину угла αо и его знак (σα >σβ)?
(а) tg2 αо = (в) tg2 αо =
5. В площадках чистого сдвига касательные напряжения τ: (а) равны σ; (б) экстремальны; (в) равны нулю; (г) равны 6. Сколько главных площадок можно выделить вблизи точки в общем слу-чае (объемное напряженное состояние)?
(а) одну; (б) шесть; (в) три; (г) бесконечное множество.
7. В случае плоского равноосного растяжения, сколько главных площадок можно выделить?
(а) две; (б) три; (в) одну; (г) бесконечное множество.
8. Для указанных плоских напряженных состояний (а,б,в,г) – установите соответствие для главных напряжений (д,е,ж,з) и угла αо (и,к,л,м)
(д) (34.1; 5.9) (е) (100.7; -40.7) (ж) 31.2; -51,2) (з) (25; -25) (и) –22.5 (к) –26.5
|
|||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 441; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.181.90 (0.008 с.) |

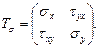

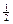 (σ x – σ y)sin2α + τcos2α. Рис. 4.2
(σ x – σ y)sin2α + τcos2α. Рис. 4.2 (σ x – σ y) sin2α0 + τcos2α0 = 0,
(σ x – σ y) sin2α0 + τcos2α0 = 0,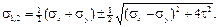
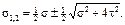
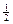 (σ1− σ2), что соответствует выражению
(σ1− σ2), что соответствует выражению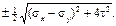
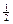 (σ1 − σ2)sin2α.
(σ1 − σ2)sin2α. При α = 45° и σ2 = −σ1 = −σ имеем τ α = σ, σ α = 0. Такое напряженное состояние называется чистым сдвигом, а площадки – площадками чистого сдви-га.
При α = 45° и σ2 = −σ1 = −σ имеем τ α = σ, σ α = 0. Такое напряженное состояние называется чистым сдвигом, а площадки – площадками чистого сдви-га.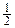 σ1sin2α.
σ1sin2α. с проекциями u, v, w на оси x, у, z, являющимися функциями координат: u = u (x, у, z), v = v (x, у, z), w = w (x, у, z). В силу сплошности тела эти функции и их частные производные требуемого порядка по x, у, z непрерывны, кроме, возможно, особых точек, линий или поверхностей.
с проекциями u, v, w на оси x, у, z, являющимися функциями координат: u = u (x, у, z), v = v (x, у, z), w = w (x, у, z). В силу сплошности тела эти функции и их частные производные требуемого порядка по x, у, z непрерывны, кроме, возможно, особых точек, линий или поверхностей.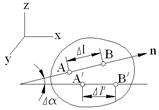 Для определения линейной деформации в точке А вдоль оси n (рис.4.4) возьмем в теле на этой оси малый отрезок АВ. После деформирования тела он обратится в отрезок А'В', составляющий с отрезком АВ угол ∆α, и будет иметь длину ∆ l '. Исходя из незначительного изменения геометрических характеристик тела в результате деформирования, можно считать Рис. 4.4
Для определения линейной деформации в точке А вдоль оси n (рис.4.4) возьмем в теле на этой оси малый отрезок АВ. После деформирования тела он обратится в отрезок А'В', составляющий с отрезком АВ угол ∆α, и будет иметь длину ∆ l '. Исходя из незначительного изменения геометрических характеристик тела в результате деформирования, можно считать Рис. 4.4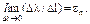
 Положительными принимают линейную деформа-цию, соответствующую растяжению, и деформацию сдвига, отвечающую уменьшению первоначального угла пересечения отрезков.
Положительными принимают линейную деформа-цию, соответствующую растяжению, и деформацию сдвига, отвечающую уменьшению первоначального угла пересечения отрезков.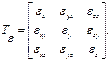
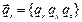 имеют вид
имеют вид 
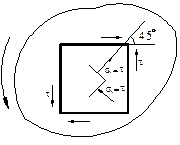 Решение: σгл.=0±
Решение: σгл.=0±  = ±
= ± 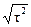 = ± τ.
= ± τ.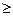 σ2
σ2 
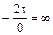 ; 2αоarctg
; 2αоarctg 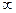 = 90
= 90 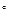 ; αо=45
; αо=45 
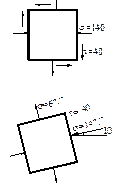 2. Определить величину и направление главных напряжений для случая плоского напряжённого состояния, показанного на рисунке:
2. Определить величину и направление главных напряжений для случая плоского напряжённого состояния, показанного на рисунке: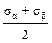 ±
± 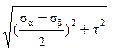 и tg2αо= -
и tg2αо= - 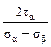
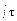 dx знак τ > 0 будет в случае,
dx знак τ > 0 будет в случае,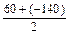 ±
± 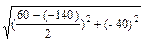 = - 40 ± 107.7.
= - 40 ± 107.7.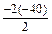 =
= 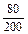 = 0.4; 2αо= arctg0.4 = 21.2
= 0.4; 2αо= arctg0.4 = 21.2 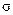 и
и  при повороте площадки на угол
при повороте площадки на угол  в случае плоского напряженного состояния?
в случае плоского напряженного состояния?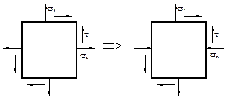 (а) уменьшится, но сохранит знак;
(а) уменьшится, но сохранит знак; 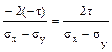 , а во втором tg2 αо=
, а во втором tg2 αо= 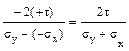 .
.
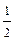 (σα-σβ)∙ sin2α, то экстремальное значение τ примет при sin2α =1(α=45
(σα-σβ)∙ sin2α, то экстремальное значение τ примет при sin2α =1(α=45  ), а величина τэкстр.=
), а величина τэкстр.= 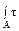 ХZdA;
ХZdA;  (е) =
(е) = 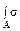 Х ZdA; (ж) =
Х ZdA; (ж) = 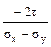 ;
;  .
.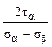 ; (б) tg2 αо =
; (б) tg2 αо = 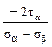 ;
;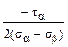 ; (г) tg2 αо =
; (г) tg2 αо = 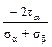 ;
;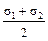 .
.



