
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения равновесия для внутренних усилий в поперечных сечениях стержнейСтр 1 из 23Следующая ⇒
В общем случае нагрузка на стержень может быть задана интенсивностью сил с составляющими
Рис. 2.3
Из условий
Из условий
откуда, пренебрегая бесконечно малыми второго порядка, находим
Подставляя выражения
Интегрируя полученные шесть уравнений, находим выражения для внутренних усилий:
Постоянные интегрирования С i (i =1,2,...,6) определяются из граничных условий для рассматриваемых внутренних усилий. Поскольку дифференциальные уравнения выражают равновесие любого бесконечно малого элемента стержня, то удовлетворение им означает выполнение условий равновесия стержня в целом. Дифференциальные зависимости используются для проверки результатов, полученных с помощью алгебраических уравнений равновесия. Они позволяют, например, по эпюре
можно установить, что при М z = const имеем Qy = 0(при М y =const имеем Q z = 0). Переменная величина При определении внутренних усилий из уравнений равновесия целесообразно нагрузку на поверхности переносить в соответствующие точки на оси стержня с соблюдением условий статической эквивалентности. Полученная таким образом силовая схема является составной частью так называемой расчетной схемы (системы), когда брус представляется его осью. Практикум Примеры: 1. Построить эпюры поперечных сил и изгибающих моментов для балки (рис.2.4, а). а б в
Рис. 2.4 Решение. Определяем реакции опор А и В: ∑ МА = 20 – 10 ∙ 4 ∙ 2 – 30 ∙ 2 + R В ∙ 6 = 0 ; R В = 20 кН; ∑ МВ = 20 – R А ∙ 6 + 10 ∙ 4 ∙ 4 + 30 ∙ 4 = 0; R А = 50 кН. Проверка: ∑ Y = 50 – 10 ∙ 4 – 30 + 20 = 0. На 1 участке (0 ≤ х ≤ 2м): Qy = 50 – 10 x (прямая с граничными значениями 50 кН при х = 0 и 30 кН при х = 2 м); М z = –20 + 50 x – 0,5 ∙ 10 x 2 (парабола с граничными значениями –20 кН∙м при х = 0 и 60 кН∙м при х = 2 м).
На 2 участке (2 ≤ х ≤ 4 м): Qy = 50 – 10 x – 30 (прямая с граничными значениями 0 при х = 2 м и –20кН при х = 4 м); М z = –20 + 50 x – 0,5 ∙ 10 x 2 – 30 (х – 2) (парабола с граничными значениями 60 кН∙м при х = 2 м и 40 кН∙м при х = 4 м). На 3 участке (4 ≤ х ≤ 6м): Qy = 50 – 10 ∙ 4 – 30 = –20кН (прямая, параллельная оси х); М z = –20 + 50 x – 10 ∙ 4 (х –2) – 30 (х –2) = 120 – 20 х (прямая с граничными значениями 40 кН∙м при х = 4 м и 0 при х = 6 м). Qy = –20 кН и Mz = 0 при x = 6 м отражают граничные условия на опоре В. Эпюры Qy и Mz показаны на рис.2.4, б, в.
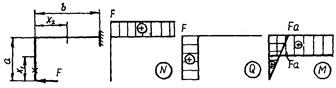
Пример 2.2. Построить эпюры N, Q и М для ломаного бруса (рис.2.5, а).
а б в г Рис. 2.5 Решение. Брус имеет два участка. Первый участок – вертикальный элемент бруса (0 ≤ х 1≤ а). Условимся нижнюю его часть считать левой частью (отмечена крестиком). Внутренние усилия в сечении с абсциссой х 1 равны: N = 0, Q = F, M = Fx 1. При x 1 = 0 М = 0, при х 1 = а М = F а. Второй участок − горизонтальный элемент бруса (0 ≤ х 2≤ b). В сечении с абсциссой х 2 внутренние усилия вычисляем из условий равновесия левой части: N = F, Q = 0, М = F а. По полученным значениям строим эпюры N, Q и М (рис.2.5, б−г). Вопросы для повторения
1. Что называют внутренними усилиями? 2. Как определяют внутренние усилия? 3. Какие правила знаков приняты для каждого из внутренних усилий? 4. Являются ли реакции опор внутренними усилиями? 5. Зачем строят график распределения внутренних усилий (эпюру)? 6. В чем суть метода сечений? 7. Какая особая точка в сечении принимается за центр приведения внутренних сил? 8. Какую из отсеченных частей более целесообразно рассматривать в равновесии? Почему? 9. Какие внутренние усилия возникают в поперечных сечениях бруса в случае действия на него плоской системы сил? 10. Как вычисляются продольная и поперечная силы в сечении? 11. Как вычисляется изгибающий момент? 12. Какие типы опор применяются для закрепления балок к основанию? 13. Какие внешние реактивные силы возникают в различных опорах? 14. Какие уравнения используют для определения опорных реакций?
15. Как проверить правильность определения реакций?
16. Каких правил придерживаются при построении эпюр? 17. Можно ли для двухопорной балки определить внутренние усилия без вычисления реакций опор? 18. Почему при построении эпюр Q, M для балки, защемлённой одним концом, можно не определять реакции опоры? 19. Какая дифференциальная зависимость связывает q, Q и M?
Тесты для повторения 1. Сколько уравнений статики необходимо составить для определения реакций двухопорной балки? (а) два; (б) три; (в) четыре; (г) шесть. Ответ: (б), поскольку в общем случае для плоской системы сил можно составить три независимых уравнения статики, из которых и определяют три неизвестных реакций опор. Четвёртое уравнение используют для проверки пра-вильности решения.
(а) Q = q; (б) Q = q x; (в) Q= -q x; (г) Q= q x -q l 2. Ответ: (б) поскольку поперечная сила в сече-
3. Для той же расчётной схемы аналитическое выражение для изгибающего момента Mz: (а) Ответ: (в), поскольку в соответствии с правилами знаков Me=q l 2 даёт положительную компоненту, а составляющая момента от распределённой наг-рузки
4. Для расчётной схемы аналитическое выра-жение для поперечной силы на левом участке имеет вид: (а) q x -F; (б) q l +F; (в) -q x -F; (г) q l -F. Ответ: (г),поскольку накопившееся на правом участке составляющая попере- чной силы от равномерно распределённой нагрузки q l входит со знаком плюс, а сила F даёт отрицательную компоненту.
5. В расчётной схеме п.4 выражение для изгибающего момента M z: (а) –q l ( Ответ: (а), поскольку компонента от сосредоточенной силы F даёт составляющую (+F x), а накопившаяся на правом участке сила q l, будучи заме-нена равнодействующей, приложенной посередине правого участка, даёт соста-вляющую q l (
6. Что возникает на эпюре поперечных сил Q в сечении, где приложена сосредоточенная сила F? (а) прежде постоянные значение эпюры Q становится переменным; (б) скачок на величину силы F и в направлении (в) изменяется наклон прямой линии эпюры Q; (г) не отмечается изменений. Ответ: (б), поскольку в отличие от предшествующего участка в аналитической зависимости для Q возникает ещё одна составляющая, равная F, то на эпюре в этом сечении скачок на величину F, и в направлении этой силы (если движемся слева).
7. Что возникает на эпюре изгибающих моментов М в сечении, где приложена сосредоточенная сила F?
(а) изменений нет; (б) эпюра моментов претерпевает скачок на величину F; (в) эпюра моментов становится линейной; (г) излом эпюры М на “острие” вектора Ответ: (г), поскольку Q =
8. Что возникает на эпюре поперечных сил в сечении, где приложена внешняя пара сил Ме? (а) скачок на величину Ме; (б) эпюра М меняет значение на противоположное; (в) изменений нет; (г) изменяется наклон эпюры. Ответ: (в), поскольку пара сил не проектируется на ось, то и на эпюре Q изменений нет.
9. Что возникает на эпюре изгибающих моментов М в сечении, где приложена внешняя пара сил Ме? (а) изменений нет; (б) отмечается изменение угла наклона касательной к эпюре М; (в) скачок на величину Ме в сторону сжимаемого этой парой “волокна”; (г) скачок на величину Ме в сторону растягиваемого этой парой “волокна”. Ответ: (г), поскольку в аналитической зависимости для изгибающего момента при переходе сечения, где приложена Ме возникает новое слагаемое, то на эпюре – скачок на величину Ме в ту сторону, какое “волокно” дорастягивает Ме (в соответствии с правилом знаков).
10. Если переходим с участка, на котором заканчивается действие равномерно распределённой нагрузки q, то на эпюре изгибающих моментов М: (а) происходит изменение угла наклона линейной эпюры; (б) криволинейная эпюра изменяет кривизну на противоположную; (в) эпюра М остаётся неизменной по характеру; (г) прежде криволинейная эпюра становится линейной. Ответ: (г), поскольку в аналитической зависимости при переходе на участок, где q =0, исчезает слагаемое, содержащая компоненту
11. На участке, где имеется равномерно распределённая нагрузка и эпюра изги-бающих моментов изменяется по квадратичной зависимости, то наличие экстремума (Мэкстр.) обусловлено: (а) изменением знака функции М(х); (б) равенством нулю поперечной силы в пределах участка; (в) равенством нулю производной (г)изменением характера функции М(х). Ответ: (б), поскольку равной нулю функция М(х) имеет экстремум.
12. Условием определения (в пределах участка) положения сечения, где М = Мэкстр. является:
(а) Ответ: (в), поскольку именно в сечении, где Q=0, а следовательно и касатель-ная функции М(х), тангенс угла наклона которой равен производной
Контрольные тесты
1. Построить эпюры Q, M и определить Qмax, Mмax.
(1.1) Qмax [кH]: (а) 10; (б)35 (в)40; (г)55. Mмax [кHм] (д) 40; (е) 41.5; (ж)20; (з) 37.5.
(1.2) Qмax [кH]: (а) 20; (б)30; (в)40; (г)50. Mмax [кHм] (д) 20; (е) 30; (ж)40; (з) 50.
(1.3) Qмax [кH]: (а) 20; (б)35; (в)45; (г)50. Mмax [кHм] (д) 52.5; (е) 63.5; (ж)40; (з) 42.5.
(1.4) Qмax [кH]: (а) 15; (б)20; (в)25; (г)40. Mмax [кHм] (д) 10; (е) 20; (ж)30; (з) 40.
(1.5) Qмax [кH]: (а) 20; (б)30; (в)40; (г)60. Mмax [kH м] (д) 20; (е) 30; (ж)40; (з) 60.
3. Для расчётных схем а, б, в, г найдите соответствующие эпюры (д, е, ж, з) поперечных сил и эпюры (и, к, л, м) изгибающих моментов (длина каждого участка – l, Ме=q l 2).
[4.1] (а) 30; (б) 35; (в) 40; (г) 45. [4.4] (а) 30; (б) 35; (в) 40; (г) 45. [4.2] (а) 70; (б) 76.25; (в) 78.25; (г) 90.25. [4.5] (а) 12.5; (б) 20; (в) 25; (г) 30. [4.3] (а) 15; (б) 30; (в) 45; (г) 60.
|
|||||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 197; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.51.3 (0.059 с.) |
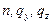 , и интенсивностью моментов с составляющими
, и интенсивностью моментов с составляющими 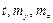 . Возможна также нагрузка, сосредоточенная в отдельных точках. Для бесконечно малой части стержня (рис.2.3) составим дифференциальные уравнения равновесия.
. Возможна также нагрузка, сосредоточенная в отдельных точках. Для бесконечно малой части стержня (рис.2.3) составим дифференциальные уравнения равновесия.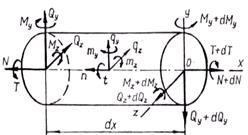
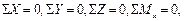 следуют уравнения:
следуют уравнения: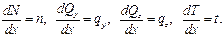
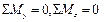 получаем:
получаем: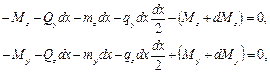
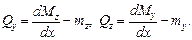
 в соответствующие дифференциальные уравнения, получаем
в соответствующие дифференциальные уравнения, получаем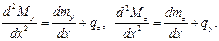

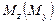 определить характер эпюры
определить характер эпюры 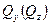 . В частности, на участках, где
. В частности, на участках, где 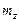 =0 (
=0 (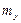 =0), т.е. при соблюдении зависимостей
=0), т.е. при соблюдении зависимостей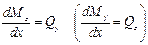
 достигает экстремальных значений в точках, где Qy = 0(Qz = 0).
достигает экстремальных значений в точках, где Qy = 0(Qz = 0).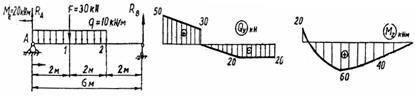
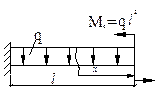 2. Для расчётной системы аналитическое выражение для поперечной силы:
2. Для расчётной системы аналитическое выражение для поперечной силы:  нии равна сумме проекций сил на ось “y”, приложенных к рассматриваемой части балки (qx). Ответ (в) не соответствует правилу знаков для поперечной силы, а в ответе (г) присутствует Me= q l 2, но пара сил не даёт проекцию на ось.
нии равна сумме проекций сил на ось “y”, приложенных к рассматриваемой части балки (qx). Ответ (в) не соответствует правилу знаков для поперечной силы, а в ответе (г) присутствует Me= q l 2, но пара сил не даёт проекцию на ось.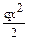 +q l 2; (б)
+q l 2; (б) 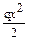 не растягивает нижнее волокно, следовательно даёт отрицатель-ную составляющую.
не растягивает нижнее волокно, следовательно даёт отрицатель-ную составляющую.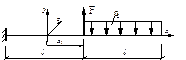
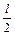 + x)+F x; (б) -
+ x)+F x; (б) - 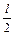 + x) со знаком “минус”.
+ x) со знаком “минус”.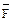 (если движемся слева);
(если движемся слева);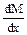 , а эпюре Q в этом сечении скачкообразно изменяет своё значение (см. п.6), то изменяется и угол наклона касательной (проходит излом на “острие” вектора F).
, а эпюре Q в этом сечении скачкообразно изменяет своё значение (см. п.6), то изменяется и угол наклона касательной (проходит излом на “острие” вектора F).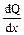 ;
;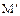 =
= 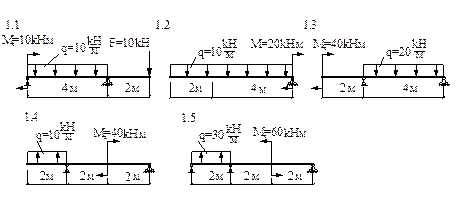
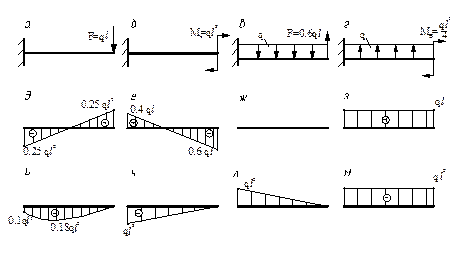 2. Для расчётных схем а, б, в, г найдите соответствующие эпюры (д, е, ж, з) поперечных сил и эпюры (и, к, л, м) изгибающих моментов (длина балки – l).
2. Для расчётных схем а, б, в, г найдите соответствующие эпюры (д, е, ж, з) поперечных сил и эпюры (и, к, л, м) изгибающих моментов (длина балки – l).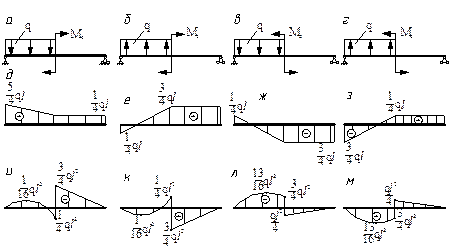
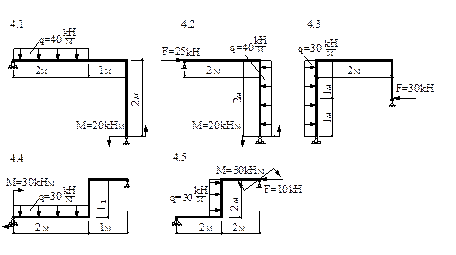 4. Построить эпюры изгибающих моментов и определить Ммах:
4. Построить эпюры изгибающих моментов и определить Ммах:


