
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поверочные и проектные расчетыСодержание книги
Поиск на нашем сайте
Смысл поверочного расчета по методу допускаемых напряжений состоит в сопоставлении фактических напряжений в опасном сечении бруса с допускаемыми:
Здесь и в дальнейших поверочных и проектных расчетах внутренние усилия берутся по модулю. Это неравенство называется условием безопасной прочности при растяжении (сжатии). Фактические напряжения не должны отклоняться от допускаемых более, чем на 5%. Большее перенапряжение недопустимо с точки зрения безопасной прочности, а недонапряжение приводит к перерасходу материала. Обратные задачи решаются при заданном допускаемом напряжении. В первом случае заданными считаются также размеры поперечного сечения, а определяется допускаемая продольная сила:
Во втором случае при известной нагрузке определяется площадь поперечного сечения
после чего вычисляют его размеры. Если их количество больше единицы, необходимы дополнительные соотношения между ними (например, отношение высоты прямоугольника к ширине). Наиболее экономичным является брус равного сопротивления. Он имеет переменную по длине площадь поперечного сечения, подобранную так, что напряжения во всех сечениях одинаковы: σ x = σ adm.
A 0 = F/ σ adm. Чтобы установить закон изменения площади сечения по высоте бруса, возьмем два смежных сечения. Приращение площади dA (x) при переходе от одного сечения к другому должно воспринять вес ρ gA (x) dx элемента бруса между сече-ниями при том же напряжении: Рис. 7.4 откуда
После интегрирования получаем
Подставим значение А (х) = Ао при х = 0: l n А 0 + С = 0, и С =– l n A 0. Окончательно А (х) = A 0exp[(ρ gx)/σ adm ]. Криволинейность границы бруса удорожает его изготовление. На практике чаще применяют стержни ступенчатые или в виде усеченного конуса. Приведенный проектный расчет является приближенным. Предполагалось, что по всему сечению бруса передаются только нормальные напряжения; на самом деле у краев сечения напряжения будут направлены по касательной к боковой поверхности. Установлено, что формулу напряжений для бруса постоянного сечения можно применять с достаточной точностью для бруса переменного сечения, если угол конусности α ≤ 12º. Важно заметить, что, рассматривая условия безопасной прочности, мы не предполагали отклонения от определенной начальной формы равновесия стержня. Эта проблема будет рассматриваться в гл. 13. Помимо условия прочности, требуется выполнение условия жесткости: N /(EA) ≤ ε adm. Решения обратных задач имеют вид: Nadm ≤ EA ε adm, A ≥ N /(E ε adm), E ≥ N /(A ε adm). Легко заметить, что первые две формулы в случае совпадения величин E ε adm и σ adm будут тождественны соответствующим формулам, полученным из условия прочности, а в случае несовпадения –отличаться на постоянный множитель. Третья формула определяет новый тип проектной задачи – подбор материала с необходимыми упругими свойствами. При расчете по предельным состояниям вместоσ adm принимаются расчетныесопротивления растяжению(Rt) или сжатию (Rc). 7.6 Практикум Примеры
1. Для стального бруса (Е=2 мальных напряжений в поперечных сечениях бруса и перемещения этих сече- ние.
NDL=0; NBC=60 кH; NAB=60+120=180 кH. По полученным значениям строим эпюру продольных сил N (рис.б) В поперечных сечениях бруса воз-никают нормальные напряжения. σDL= σCD= =12 σВС= По полученным значениям строим эпюру нормальных напряжений σ (рис.в). Поперечные сечения бруса под действием внешних сил смещаются впра-во относительно неподвижного сечения А. Величина на участке АВ при (0
на участке ВС при (0
на участке АВ при (0
Участок DL не деформируется (NDL=0, следовательно Во всех полученных выражениях переменная х входит в первой степени, а следовательно зависимость между Поскольку
2.1 Стержень изготовлен из плас-тичной стали: σadm=160 МПа, F=40 кН. Подобрать площади поперечных сечений для каждого из участков. Решение. Условие безопасной прочности σ = А1 А2 Для второго участка, где N2 <0 берём абсолютное значение силы 120 кН и делим на допускаемое напряжение σadm=160 МПа, которое для пластичных ма- териалов имеет одинаковое значение и в случае растяжения, и в случае сжатия. Принимаем: А1=12.5 см2; А2=7.5 см2; А3=5 см2.
2.2 Стержень изготовлен из чугуна: σadm t=120 МПа; σadmс=310 МПа; F=50 кН; А1=25 см2; А2 =; А3=? Проверить прочность стержня. Дать рекомендации по изменению поперечных сечений (рациональные сечения). Решение. Определим напряжения на каждом участке σ1 σ3= На втором участке σ2= На третьем участке σ3=125 МПа
2.3 Стержень изготовлен из пластичной стали: σadm=160 МПа; А1=30 см2; А2=15 см2; А3=20 см2. Определить допускаемое зна-чение нагрузки F. Решение. Следует сравнить напряжения на каждом из трёх участков и из усло-вия безопасной прочности σмах= σ 1 На втором участке нормальные напряжения наибольшие по абсолютному зна-чению, поэтому, наибольшее значение силы Fмах. =8·104 Н = 80 кН. Допускаемая величина силы Fadm= 80 кН. При таком значении силы на втором участке нормальные напряжения равны σadm, а на первом и втором участке они соответственно составляют 83.5% и 50% от σadm. Вопросы для повторения
3. Как вычисляется значение продольной силы N в произвольном поперечном сечении бруса?
5. Как распределены нормальные напряжения σх в поперечных сечениях центрального растянутого бруса и чему они равны? 6. В каких сечениях растянутого бруса возникают наибольшие нормальные напряжения?
8. Как формулируется закон Гука? Запишите формулы абсолютной и относительной продольной деформации бруса?
10. Как учитывается собственный вес бруса в аналитическом выражении для продольной силы? 11. Как объяснить наличие множителя 1/2 в формуле удлинения вертикального бруса постоянного сечения от собственного веса?
13. Как назначаются допускаемые напряжения для пластичных и хрупких материалов?
15. Какие три характерных вида задач встречаются при расчете на прочность конструкции? 16. Почему считается возможным отклонение до 5% фактического напряжения от допустимого? 17. Почему необходимо выполнять условие жесткости? Приведите приме-ры. 18. При проведении расчета на прочность по предельным состояниям с чем сравнивают фактические напряжения?
Контрольные тесты
1. В поперечном сечении растянутого бруса возникают напряжения, которые называются …
3. Безопасная прочность бруса при растяжении определяется по формуле… 4. Допустимые напряжения для пластичных материалов определяют по формуле … 5. Допустимые напряжения при растяжении хрупких материалов определяют по формуле … 6. Опасным поперечным сечением бруса является сечение, в котором действуют наибольшие … 7. Центральным растяжением называют такой вид деформации, при котором в поперечном сечении возникает только одно внутреннее усилие - … 8. С увеличением жесткости поперечного сечения бруса абсолютное удлинение … 9. Площадь поперечного сечения бруса из условия безопасной прочности при растяжении определяется по формуле … 10. Значение продольной силы в поперечном сечении бруса вычисляют из условия …
16. Отличие расчета на прочность по предельным состояниям от расчета по допустимым напряжениям состоит в … СДВИГ 8.1 Основные положения
Исследуя в п.4.2 плоское напряженное состояние, мы установили, что если главные напряжения равны по величине и противоположны по знаку, то площадки, наклоненные к главным под углом 45°, являются площадками чистого сдвига (рис. 8.1).
Чистый сдвиг прямоугольного призматического бруса вызывается поперечными силами по четырем его граням. На рис. 8.2 показан чистый сдвиг в плоскости ху. Зададим следующие условия: 1) отсутствуют линейные деформации, а следовательно, нормальные напряжения и соответствующие им внутренние усилия в поперечных сечениях бруса (продольная сила и изгибающие моменты); 2) отсутствует деформация сдвига γ zx, а следовательно, τ zx =τ xz = 0, Qz = 0; 3) сечение остается плоским, т.е. γ xy = const; 4) физический закон − закон Гука при сдвиге; из него вытекает, что τ yx = τ xy = const; как следствие, крутящий момент при совмещении центра приведения с центром тяжести обращается в нуль; 5) задана величина поперечной силы Qy. Рис. 8.1 Рис. 8.2
Для определения напряжений, деформаций и перемещений привлекаем зависимости по трем законам деформирования для τ xy и γ xy:
За основное неизвестное принимаем деформацию сдвига γ xy. При малых величинах γ xy можно пренебречь перемещениями v и принять γ xy = ∂ u /∂ y. Так как u – функция одной переменной у, то γ xy =du/dy, откуда
Из условия неподвижности нижней грани (u = 0 при y = 0) вытекает С = 0, и следовательно, u = γ xy y. Интегральное уравнение при τ xy = const принимает вид Qy = τ xy A, откуда τ xy = Qy /A. Обращаясь к физическому закону, находим γ xy = Qy / (GA), и окончательное выражение для перемещений u = (Qyy) / (GA). Анализируя полученное решение, проведем некоторые параллели между сдвигом и растяжением (сжатием): 1. На торцах на основании статического граничного условия постоянное напряжение трансформируется в равномерно распределенную нагрузку YP = τ xy, которая и соответствует рассмотренной деформации чистого сдвига. На основании свойства парности касательных напряжений по двум взаимно перпендикулярным площадкам на соответствующих продольных гранях также имеет место равномерно распределенная нагрузка Х P = τ yx = τ xy (в этом отличие сдвига от растяжения). Равнодействующие Qx и Qy связаны между собой соотношением Qy / Qx = h / l. 2. Напряжение τ xy прямо пропорционально Qy и обратно пропорционально А. Следовательно, при заданной поперечной силе напряжение можно уменьшить путем увеличения площади поперечного сечения. 3. Деформация сдвига обратно пропорциональна величине GA, называемой жесткостью при сдвиге.
8.2. Практические расчёты соединений, работающих на сдвиг.
Для многих соединений, таких как свар-ные, болтовые заклёпочные, работающих в сложных напряжённых состояниях оценка работоспособности может быть проведена простыми, но довольно надёжными расчё-тами на сдвиг. Изучив начальную стадию разрушения Рис. 8.3 наблюдать, что происходит срез тела заклё- пки по плоскостям соприкосновения листов. Количество площадок среза n наединицу меньше числа соединяемых листов и пропорционально суммарному числу заклёпок в соединении k. Аср= Условия безопасности прочности если расчёт ведём по допускаемым напряжениям. При расчёте по предельным состояниям действующие напряжения среза τ сравнивают с расчётным сопротивлением материала заклёпки на срез Rср. Так выполняют поверочный расчёт. При проектировании заклёпочного соединения диаметр заклёпки назначают, ориентируясь на толщину соединяемых пластин и из условия прочности определяют минимально возможное число заклёпок В заклёпочном соединении может происходить смятие отверстий листов по поверхности контакта. Это особенно важно при проектировании герметич-ных сосудов. В этом случае дополнительно выполняют проверку на смятие. До-полнительно следует проверить на растяжение и полосу, ослабленную отвер-стиями. Расчёт болтовых соединений производят в том же порядке. Расчёт высо-копрочных болтов осуществляют из условия затяжки соединения необходимым моментом затяжки, обеспечивающим требуемое усилие на контактирующих поверхностях обжимаемых листов, на которых возникающие силы трения и во-спринимают срезающие усилия. Высокопрочный болт работает только на рас-тяжение. Площадь его поперечного сечения назначается из условия безо-пасной прочности на растяжение. Сварные соединения менее трудоёмки в исполнении, не приводят к ос-лаблениям элементов, более экономичны. Сварные соединения, как и заклёпоч-ные, условно рассчитывают в предположении равномерного распределения напряжений по сечению шва.
Если сварное соединение довести до разрушения, то наплавленный мате-риал останется на обеих частях пластин (рис. 8.4 а). Рис. 8.4 Срез происходит по площадке m-m, площадке наименьшего сечения, размер которого составляет h где: Rср – расчётное сопротивление материала сварного шва на срез; l шва – расчётная длина шва (в нашем случае l шва=2 l). Для случая когда дополнительно осуществить и сварку по торцу (лобовой шов) длиной b, l шва=2 l +b.
Рис. 8.5 8.3 Практикум Примеры
1.Определить необходимое число заклёпок диаметром 1,2см для соединения “внахлёст” двух пластин толщиной 0,8см и шириной 10см, если известно, что нормальные напряжения в растянутой полосе σ =150МПа и τadm=100МПа. Решение. Если в растянутой пластине напряжения известны, то вызывавшая их сила N=σ Эта сила будет срезающей для односрезных заклёпок, число которых: k Число заклёпок для обеспечения безопасной прочности соединения должно быть не менее 11 шт.
2. Найти необходимую длину фланговых швов, соединяющих равнополочный уголок 63 Решение. Условия безопасной прочности имеет вид:
l шв
тогда l лев=14см, l пр=5.5см.
3. Две тяги соединены штырём, вставленным в проушины, и нагружены силой F=150кH. Определить действительный запас прочности, если: σу=230МПа; τу=180МПа.
Решение. Определим действующие напряжения среза в штыре
Запас прочности по касательным напряже-ниям Определим действующие нормальные напря-жения в ослабленном сечении правой пласти-ны (т.к. суммарная толщина двух левых боль-ше и там напряжения меньше)
Запас прочности по нормальным напряжениям
4. Пуансон диаметром 2см прошивает отверстие в стальной пластине толщиной 0.6см с усилием 130кН. Определить касательные напряжения в пластине и нор-мальные сжимающие напряжения в пуансоне. Решение. Площадь среза представляет собой цилиндрическую поверхность ди-аметром 2см и высотой 0.6см. Аср= π Напряжение в пуансоне
Вопросы для повторения
1.Какой случай плоского напряженного состояния называется чистым сдвигом? 2. Как записывается закон Гука при сдвиге? 3. Какие константы упругости для изотропного материала вам известны? 4. Как связаны эти константы? 5. В чём состоит закон парности касательных напряжений? 6. Как определяют величину τadm? 7. Какие упрощающие гипотезы используют при расчёте на срез? 8. Как связаны поперечная сила Q и касательные напряжения в площадке среза? 9. Как вычисляются действующие касательные напряжения в предполо-жении их равномерного распределения в сечении? 10. Запишите условие безопасной прочности при срезе. 11. Как определить действительный запас прочности, если известны дей-ствующие касательные напряжения и прочностные характеристики материала? 12. Как определить необходимое количество заклёпок, обеспечивающее безопасную прочность соединения? 13. Почему в условии прочности для сварного шва содержится множитель 0.7 катета шва? 14. Какие дополнительные проверки на прочность выполняют при расчёте заклёпочного соединения? 15. Как определяют число срезов заклёпки, соединяющих пакет из m ли-стов? 16. Почему при расчёте сварного соединения можно суммировать длины продольных и поперечных швов?
Тесты для повторения 1. Почему продольные (фланговые) швы предпочтительнее торцевых (лобовых) при ударных нагрузках? (а) их можно выполнить более качественно; (б) протяжённость таких швов неограниченна шириной полосы; (в) потому что фланговые швы разрушаются без значительных пластических деформаций; (г) фланговые швы разрушаются с образованием значительных пластических деформаций. Ответ: (г), предшествующие разрушению значительные пластические деформации могут поглощать значительно большую энергию удара, а при разрушении лобовых швов абсолютные сдвиговые деформации малы. 2. Почему в заклёпочном соединении при большом количестве заклёпок их располагают несколькими рядами, а не в один ряд? (а) заклёпки более равномерно нагружены; (б) ослабление ”живого сечения” полосы меньше; (в) все заклёпки не помещаются в один ряд; (г) на каждую заклёпку в этом случае придётся большая часть нагрузки. Ответ: (б), поскольку в этом случае ослабленная большим количеством отверстий под заклёпки полоса может не обеспечить прочность. 3. Если две пластины соединяются сваркой встык, а толщина пластины t и ширина b, то каким будет правильное условие прочности:
(в) Ответ: (в), поскольку в таком сварном шве площадка разрушения (
4. Две пластины соединены с помощью двух накладок и растянуты силой F. Катет шва h. Какая из формул будет верной при проверке на прочность?
(а) (в) Ответ: (б), поскольку при разрушении соеди-нения образуются две части и общая длина разрушенного шва будет составлять 4а, и пло-щадь среза - 0.7h∙4a.
КРУЧЕНИЕ
Основные понятия
Рис. 9.1 Рис. 9.2
Для получения наглядного представления о деформации возьмем резиновый круглый цилиндрический брус с нанесенной прямоугольной сеткой, составленной семейством концентрических окружностей и образующими. Закрепим один конец и приложим к другому момент Т e (рис.9.1). Полученная в результате деформирования сетка из параллелограммов свидетельствует о наличии сдвига. Окружности остаются неизменными, расстояния между ними не меняются. На основании гипотезы плоских и жестких сечений (см. п. 7.1) каждое поперечное сечение поворачивается в своей плоскости на некоторый угол как жесткое целое. Радиусы всех сечений будут поворачиваться, оставаясь прямолинейными. Тем самым можно предположить, что характер деформаций, наблюдаемых на поверхности, будет таким же и внутри бруса на любой цилиндрической поверхности, концентричной с наружной. Для установления геометрических соотношений рассмотрим элемент бруса (см. рис. 9.1) между сечениями I-I и II-II (сечение I-I условно закреплено) и сконцентрируем внимание на линии АВ ′ и радиусе O В ′, которые до деформации занимали положение АВ и O В (рис. 9.2). Поворот образующей АВ связан с из- менением положения радиуса OB. Угол d
Перемещение точки С на радиусе ОВ связано с поворотом образующей DC цилиндра произвольного радиуса ρ. Сопоставим длину дуги СС′ из двух вычислений: dx γθ x = ρ d откуда γθ x = (d Относительный угол закручивания назовем кривизной кручения и обозначим kt. Таким образом, имеем kt = d
|
|||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 348; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.209.100 (0.01 с.) |

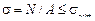 .
.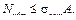
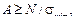
 Возьмем брус, подверженный растяжению силой F и собственным весом (рис. 7.4). Площадь нижнего сечения А 0 определяется из условия F /А 0 = σ adm:
Возьмем брус, подверженный растяжению силой F и собственным весом (рис. 7.4). Площадь нижнего сечения А 0 определяется из условия F /А 0 = σ adm: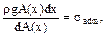
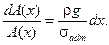
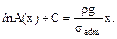
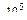 МПа) построить эпюры продольных сил, нор-
МПа) построить эпюры продольных сил, нор- Решение. Продольную силу в поперечном сечении определим проектируя внешние силы, приложенные справа от рассматриваемого сечения на ось бруса:
Решение. Продольную силу в поперечном сечении определим проектируя внешние силы, приложенные справа от рассматриваемого сечения на ось бруса: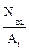 =0;
=0;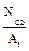 =
= 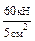 =
= 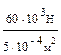 =
=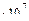 Па=120 МПа;
Па=120 МПа;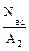 =
=  = 50 МПа; σАВ=
= 50 МПа; σАВ= 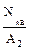 =
= 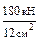 = 150 МПа.
= 150 МПа.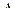 смещения сечения, ра- положенного на расстоянии х от левого конца бруса равна деформации уча-стка длинной х:
смещения сечения, ра- положенного на расстоянии х от левого конца бруса равна деформации уча-стка длинной х: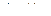 )
)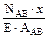 =
= 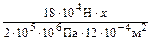 =0.75
=0.75 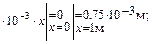
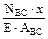 =0.75
=0.75 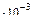 +
+ 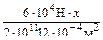
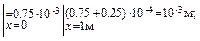
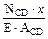 =103+
=103+ 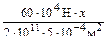 =
= 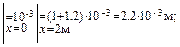
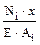 =
= 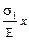 =εi· х, то относительная продольная деформация εi на каждом участке представляет собой коэффициент, соответ-ствующий углу наклона эпюры
=εi· х, то относительная продольная деформация εi на каждом участке представляет собой коэффициент, соответ-ствующий углу наклона эпюры  2. Для металлического бруса, находящегося под действием сил построена эпюра N продольных сил, возника-ющих в его сечениях. Произвести расчёт на прочность стержня в следующих случаях.
2. Для металлического бруса, находящегося под действием сил построена эпюра N продольных сил, возника-ющих в его сечениях. Произвести расчёт на прочность стержня в следующих случаях.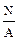
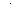 σadm позволяет вычислить минимальную площадь поперечного сечения:
σadm позволяет вычислить минимальную площадь поперечного сечения: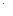
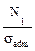 =
= 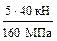 =
= 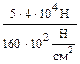 =12.5 см2;
=12.5 см2;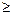
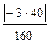 = 7.5 см2; А3
= 7.5 см2; А3 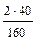 = 5 см2.
= 5 см2.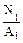 =
= 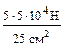 =104
=104 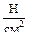 =100 МПа; σ2=
=100 МПа; σ2= 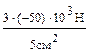 = -300 МПа;
= -300 МПа;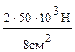 = 125 МПа. Условия безопасности прочности на первом участ-ке σ1=100 МПа
= 125 МПа. Условия безопасности прочности на первом участ-ке σ1=100 МПа 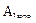
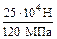 = 20.83 см3 (принимаем 21см2), тогда потребуется меньше материала для изготовления конструкции.
= 20.83 см3 (принимаем 21см2), тогда потребуется меньше материала для изготовления конструкции.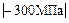
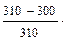 100%
100% 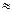 3.2%
3.2%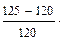 100%
100% 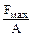
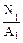 =
= 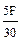 = 0.167 F; σ 2
= 0.167 F; σ 2 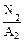 =
= 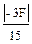 =0.2 F; σ 3
=0.2 F; σ 3 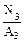 =
= 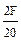 = 0.1 F.
= 0.1 F.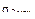
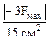 ≤ 160 МПа = σadm Fмах
≤ 160 МПа = σadm Fмах 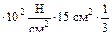 =
=
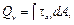 γ xy = ∂ u /∂ y +∂ v /∂ x, τ xy = G γ xy.
γ xy = ∂ u /∂ y +∂ v /∂ x, τ xy = G γ xy.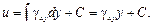

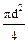
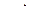 , где d – диаметрзаклёпки.
, где d – диаметрзаклёпки.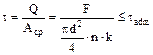 ,
,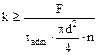
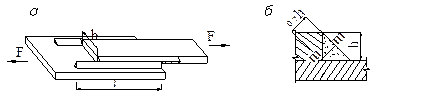
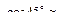 0.7 h, где h – высота катета углового шва. Ус-ловие безопасной прочности запишем в виде
0.7 h, где h – высота катета углового шва. Ус-ловие безопасной прочности запишем в виде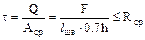 ,
, При проектировании соединения (рис. 8.5), называемого врубкой, следу-ет подобрать размеры площади abcd из условия безопасной прочности матери-ала на скол (срез), а размеры площади cefb – из условия прочности на смятие (сжатие) от действия горизонтальной составляющей силы F.
При проектировании соединения (рис. 8.5), называемого врубкой, следу-ет подобрать размеры площади abcd из условия безопасной прочности матери-ала на скол (срез), а размеры площади cefb – из условия прочности на смятие (сжатие) от действия горизонтальной составляющей силы F.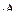 =150МПа
=150МПа 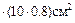 =1.5
=1.5 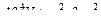 =120кН.
=120кН.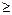
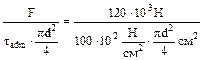 =10.6
=10.6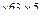 с пластиной если действующее срезающее усилие F=65кН, приняв Rср=96 МПа.
с пластиной если действующее срезающее усилие F=65кН, приняв Rср=96 МПа.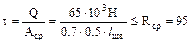 МПа (где h = 0.5см - толщина полки уголка)
МПа (где h = 0.5см - толщина полки уголка)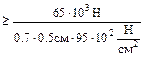 =19.5см.
=19.5см. Для обеспечения одинаковой работы левого и правого швов длины провара следует выбрать обратными расстояниям до центра тяжести сечения уголка от левого и правого шва
Для обеспечения одинаковой работы левого и правого швов длины провара следует выбрать обратными расстояниям до центра тяжести сечения уголка от левого и правого шва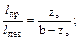
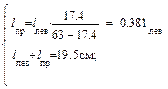
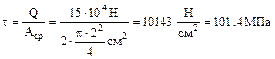

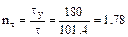
 .
. 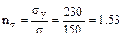 . Решением является 1.53 - меньший из двух.
. Решением является 1.53 - меньший из двух.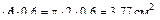
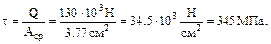
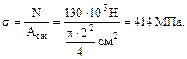
 (а)
(а) 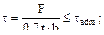 (б)
(б) 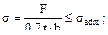
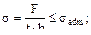 (г)
(г) 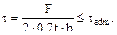
 ) и в ней действуют нормальные напряжения σ.
) и в ней действуют нормальные напряжения σ.
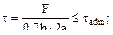 (б)
(б) 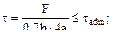
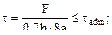 (г)
(г) 

 называется углом закручивания.
называется углом закручивания.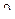 ,
,


