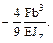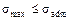Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предельное сопротивление балкиСодержание книги
Поиск на нашем сайте
Для большинства балок касательными напряжениями в поперечных сече-ниях пренебрегают. Отличие от чистого изгиба состоит только в изменении из-гибающего момента от сечения к сечению. Расположение пластических облас-тей можно определить, подставив в зависимость для граничной ординаты у y = f (Mz) выражение М z. Рассмотрим балку прямоугольного сечения в случае, когда диаграмма σ ~ ε обладает участком идеальной пластичности (см. рис.5.3, а). Читатель может убедиться, что ордината на границе упругой и пластической областей равна
Отсюда вытекает соотношение
Примем нагрузку в виде силы F, приложенной посредине балки (рис.10.11). Положив начало координат в точке под силой F, получим в случае исчерпания несущей способности в этом сечении:
А так как
Рис. 10.11 то После подстановки выражения М z в выведенное выше соотношение находим
т.е. границей раздела упругой и пластической областей является парабола. Из условия уу= h / 2 определяется расстояние, на которое простирается пластическая область по длине балки в каждую сторону от линии приложения силы: х = ± l /6. При Mz = Mz (у) получаем kx = ∞, т.е. сечение имеет безгранично нарастающие повороты. Это явление связывают с появлением так называемого пластического шарнира. Последний отличается от конструктивного тем, что, во-первых, удерживает определенный предельный момент Mz ( y ) и не препятст- ствует поворотам, начиная только с тех значений моментов, которые превосхо-дят значение Mz ( y ). Во-вторых, пластический шарнир является односторонним в процессе деформирования и исчезает при перемене знака деформации.
Практикум Следует разобрать примеры решения задач, приведенные в разделе V, контрольное задание №1. Вопросы для повторения
1. Что называют чистым и поперечным изгибом? 2. Какие внутренние усилия возникают в поперечных сечениях балки в общем случае действия на неё плоской системы сил? 3. Какие типы опор применяются? 4. Как формулируется гипотеза плоских сечений? 5. Что представляет собой нейтральный слой и нейтральная ось? 6. Чему равна кривизна оси балки при чистом изгибе? 7. Как изменяются нормальные напряжения по высоте балки при чистом изгибе? 8. Как определить максимальные нормальные напряжения при изгибе? 9. Что называют моментом сопротивления сечения при изгибе и какова его раз-мерность? 10. В каких случаях при поперечном изгибе допустимо нормальные напря-жения определять по формуле, полученной для случая чистого изгиба? 11. По какому закону изменяются касательные напряжения по высоте балки прямоугольного сечения? 12. Какие формы поперечных сечений являются рациональными для балок из пластичного материала? 13. Какой должна быть рациональная форма сечения для балки из хрупкого ма-териала? 14. Как проводится проектировочный расчет для балки заданной формы сече-ния? 15. В каких случаях следует производить дополнительный поверочный расчет по наибольшим касательным напряжениям? 16. Какие перемещения получают поперечные сечения балок при изгибе? 17. Почему при определении прогибов балки можно пользоваться приближен-ным дифференциальным уравнением изогнутой оси балки? 18. Из каких граничных условий определятся постоянные интегрирования при нахождении прогибов балки? 19. Что представляет собой уравнение метода начальных параметров? 20. Что называют композитным брусом? 21. Чем можно объяснить существенное отличие нормальных напряжений в элементах разнородной упругости при изгибе композитного бруса? 22. Чем определяется предельное состояние балки при изгибе?
Тесты для повторения
σА=: (а) 39.9 МПа; (б) 16.3 МПа; (в) 124 МПа; (г) 68.7 МПа. τА=: (д) 4.6 МПа; (е) 3.47 МПа; (ж) 1.45 МПа; (з) 6.33 МПа. Ответ: (а) и (ж). Построив эпюры Мz и Qy установим, что опасным будет сечение в задел-ке, где Мz max=38 кHм и Qy=16 кH. σк= где:
Определить как изменится фактический коэффи-цинт запаса прочности, если изгибающий момент изменит свой знак, при условии, что временное сопротивление на сжатие в четыре раза больше временного сопротивления на растяжение. (а) возрастёт в 2 раза; (б) сохранится таким же; (в) уменьшится в 2 раза; (г) уменьшится в 2.5 ра-за. Ответ: (г). Определим величину момента инерции сечения относительно оси z, установив предварительно положение центра тяжести сечения: УВ= Jz=Σ(Jzi+ Напряжение в точке С σс= Напряжение в точке В σВ= Это напряжение превышает напряжение в точке С в: Первый случай, когда в точке С изгибающий момент вызывал растягивающие напряжения более благоприятен и прочность определялась условием безопас-ной прочности в растянутой зоне (т. С) поскольку соотношение (*) меньше четырёх. Следовательно для второго случая, когда точка В будет работать в растянутой зоне фактический коэффициент запаса прочности уменьшится в 2.5 раза.
(а) σмах < σadm; (б) σмах = σadm; (в) σadm< σмах < σT; (г) σмах > σT. Ответ: (а). Определив моменты сопротивления для положения (1):
Wz=
Установим величину изгибающего момента, который вызвал напряжения 280 МПа.
Mz= σмах
В положении (2)
Wz=
следовательно σмах и напряжения
σмах=51.62 МПа < 4. К балке постоянной жёсткости Е Jz в точке С приложена сила F. Величина прогиба в этом сечении Vc,будет равна:
(в) - Ответ: (в). Определив реакцию RA= EJzV=EJz Начало координат совпадает с левой опорой, следовательно прогиб
второй начальный параметр определим из условия равенства нулю VB=0, при х = 3b. EJzV=0+EJz тогда: EJz Прогиб в точке С, находящейся на расстоянии хс =2b:
EJzVС= - тогда: VС = Контрольные тесты
1. Изгиб называется чистым, если в поперечных сечениях балки из шести внутренних усилий действуют только … 2. При изгибе возникают такие перемещения, как … 3. При поперечном изгибе в поперечных сечениях балки возникают такие напряжения, как … 4. Дифференциальная зависимость между изгибающим моментом и по-перечной силой имеет вид … 5. Когда изгибающий момент на участке с распределенной нагрузкой имеет экстремальное значение, поперечная сила в этом сечении равна … 6. Нормальные напряжения в любой точке поперечного сечения балки определяются по формуле … 7. Наибольшие нормальные напряжения в поперечном сечении балки возникают в … 8. Условие прочности по нормальным напряжениям при изгибе имеет вид … 9. Касательные напряжения при поперечном изгибе в любой точке поперечного сечения балки определяется по формуле... 10. Касательные напряжения при поперечном изгибе достигают максимума на … 11. Условие прочности по касательным напряжениям при изгибе имеет вид … 12. При упругом деформировании нейтральная линия сечения балки проходит через … 13. Момент сопротивления изгибу балки прямоугольного сечения разме-ром h ×в относительно центральной оси, параллельной основанию в равен … 14. При подборе сечения балки, его момент сопротивления должен быть не менее … 15. Моментом сопротивления изгибу поперечного сечения балки назы-вают отношение … 16. Приближенное дифференциальное уравнение упругой линии балки имеет вид … 17. Между прогибом и углом поворота сечения балки существует диф-ференциальная зависимость в виде … 18. При использовании в расчетах прогибов метода начальных пара-метров, сами начальные параметры находят из граничных условий на … 19. Если левый конец балки жестко защемлен, то начальные параметры равны … 20. Условие жесткости при изгибе имеет вид … 11. СЛОЖНОЕ СОПРОТИВЛЕНИЕ 11.1. Общие понятия
Если в поперечном сечении бруса возникают два или более внутренних силовых фактора, учитывать которые обязательно необходимо в расчетах на прочность, то говорят о сложном сопротивлении. Хотя при прямом поперечном изгибе в сечении возникают и Мz и Qу, но в подавляющем большинстве случаев расчеты на прочность и жесткость ведут без учета влияния поперечных сил, то этот случай считают простым соп-ротивлением. Если в поперечном сечении в опасной точке бруса напряженное состояние является линейным (одноосным), хотя и вызывается несколькими внутренними усилиями, то оценку прочности проводят по условию: т.е. использовать теории прочности просто не нужно. Это характерно для косого изгиба, внецентренного растяжения и сжатия. Если в опасной точке бруса возникает плоское напряженное состояние, то оценить прочность можно только по одной из теорий прочности, выбор которой определяется предельным состоянием данного материала в данных конкретных условиях нагружения (температура, скорость нагружения и т.п.). Такие расчеты проводят при изгибе с кручением, сжатии с изгибом и кручени-ем.
|
||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 198; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.57 (0.011 с.) |

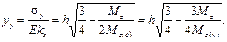

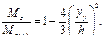
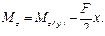
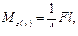
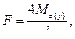
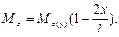
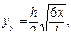
 1. Какова величина нормальных (а -г) и касательных (д -з) напряжений в опас-ном сечении в точке К?
1. Какова величина нормальных (а -г) и касательных (д -з) напряжений в опас-ном сечении в точке К?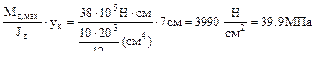 τк=
τк= 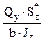 =
= 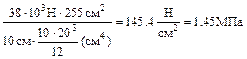 .
.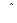 - статический момент площадки, отсекаемой сечением, проведённым через точку К параллельно плоскости (z,x);
- статический момент площадки, отсекаемой сечением, проведённым через точку К параллельно плоскости (z,x); 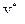 -координата центра тяжести этой площадки; b – ширина сечения.
-координата центра тяжести этой площадки; b – ширина сечения.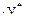 =10
=10 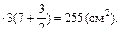
 2. Чугунная балка таврового сечения нагружена изгибающим моментом, дей-ствующим в вертикальной плоскости и растягива-ющим верхние волокна.
2. Чугунная балка таврового сечения нагружена изгибающим моментом, дей-ствующим в вертикальной плоскости и растягива-ющим верхние волокна.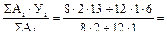 =10 см. Тогда:
=10 см. Тогда: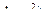 =
= 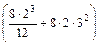 +
+ 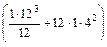 =485см4.
=485см4.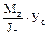 =
= 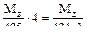 .
.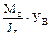 =
= 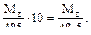
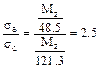 раза. (*)
раза. (*) 3. Под действием нагрузки в вертикальной плоскости в балке, поперечное сечение которой изображено (1), возникает текучесть, σмах=280МПа > σТ = 240 МПа. В каком состоянии окажется та же балка, если её расположить в положении (2), если нормативный коэффициент запаса nadm=1.5?
3. Под действием нагрузки в вертикальной плоскости в балке, поперечное сечение которой изображено (1), возникает текучесть, σмах=280МПа > σТ = 240 МПа. В каком состоянии окажется та же балка, если её расположить в положении (2), если нормативный коэффициент запаса nadm=1.5?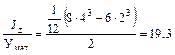 см3
см3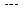 =180 МПа
=180 МПа 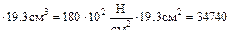 Н
Н 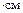
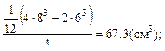
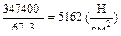 =51.62 МПа,
=51.62 МПа,
 (а) -
(а) - 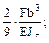 (б) -
(б) - 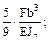
 (г) -
(г) - 
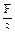 запишем универсальное уравнение ме-тода начальных параметров:
запишем универсальное уравнение ме-тода начальных параметров: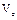 +EJz
+EJz 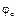 x + RA
x + RA 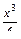 -F
-F 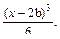
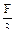
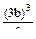 -F
-F 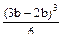
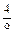 Fb2.
Fb2.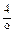 Fb2(2b)+
Fb2(2b)+ 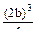 =
=