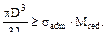Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Чистый изгиб с растяжением (сжатием)Содержание книги
Поиск на нашем сайте Эту деформацию представим себе как сочетание косого изгиба и чистого сжатия, при котором напряжения суммируются алгебраически:
Тождественную схему деформирования наблюдаем в случае приложения продольной нагрузки F со смещением (эксцентриситетом) относительно центра тяжести поперечного сечения, в точке (zF, yF) (рис.11.2, а). Этот случай получил название внецентренного сжатия 1.
После введения радиусов инерции формула принимает вид
Так как в точках нейтральной оси сечения σ x = 0, то уравнение этой оси будет Рис. 11.2
. 1Все выводы, относящиеся к внецентренному сжатию бруса, могут быть применены и к случаю внецентреннего растяжения при замене сжимающей силы -F на +F. После подстановки в уравнение этой прямой линии последовательно значений координат точки на оси у: z 0 = 0 и у 0 = a у и на оси z: у 0 = 0 и z 0 = az получаем отрезки:
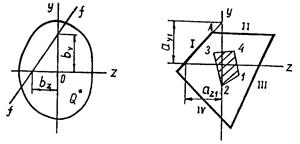
Минусы указывают на то, что нулевая линия и точка приложения силы F (полюс) располагаются по разные стороны от центра тяжести (рис.8.13, б). Докажем следующую теорему: при перемещении полюса по прямой нулевая линия вращается около неподвижной точки. Пусть f – f есть прямая, отсекающая отрезки b у и bz на осях координат (рис.11.3). Примем ее за нулевую линию, тогда координаты соответствующего полюса – точки Q суть
Если, наоборот, силу приложить в точке на линии f – f, то согласно упомянутой выше теореме, напряжение в точке Q окажется равным нулю. Совокупность нулевых линий для всех положений полюса на линии f – f есть пучок прямых, проходящих через точку Q.
Рис. 11.3 Рис.11.4
В частном случае, когда полюс движется по прямой, проходящей через центр тяжести, нулевая линия перемещается параллельно себе, ибо пропорциональное изменение координат у F и zF влечет также пропорциональное изменение отрезков а y и а z. При у F → 0 и zF → 0 нулевая линия уходит в бесконечность, что соответствует наступлению чистого растяжения (сжатия). При у F → ∞ и zF → ∞ а y → 0 и а z → 0, что соответствует наступлению чистого косого изгиба. В окрестности центра тяжести существует область, называемая ядром сечения. Если след силы F (или равнодействующей нескольких сил) находится внутри этой области, то нейтральная линия проходит за пределами сечения, и, следовательно, во всех его точках напряжения будут одного знака. Покажем построение контура ядра сечения. Пусть нулевая линия совпадает со стороной I контура сечения, отсекая на осях у и z отрезки а y 1 и а z 1 (рис.11.4). Тогда координаты точки 1 на контуре ядра сечения:
При совпадении нулевой линии с гранью II таким же способом находим координаты точки 2 (zF 2 и у F 2) на контуре ядра сечения. При вращении нулевой линии вокруг вершины А соответствующая ей точка приложения силы F перемещается вдоль отрезка 1–2. Контур ядра сечения будет многоугольником, число сторон которого равно числу сторон сечения бруса. Читателю предлагается установить, что для прямоугольного сечения с размерами b и h ядро сечения имеет форму ромба с диагоналями, равными b / 3 и h / 3, а для круга радиусом r − концентрический круг радиусом r / 4. Зная контур ядра сечения, можно определить, будут ли напряжения при заданном положении силы F иметь одинаковые или разные знаки в пределах поперечного сечения бруса. Это важно знать для материалов, не обладающих одинаковой прочностью на растяжение и сжатие. Такими являются бетон, чугун, кирпичная кладка и др.
11.4. Изгиб с кручением брусьев круглого сечения Такое сочетание внутренних силовых факторов характерно при расчете валов. Задача является плоской, поскольку понятие «косой изгиб» для бруса круглого поперечного сечения, у которого любая центральная ось является главной- неприменимо. В общем случае действия внешних сил такой брус ис-пытывает сочетание следующих видов деформации: прямого поперечного изгиба, кручения и центрального растяжения (сжатия). На рис. 11.5 показан брус, нагруженный внешними силами, вызывающими все четыре вида дефор-мации. Эпюры внутренних усилий позволяют выявить опасные сечения, а эпюры напряжений – опасные точки в этих сечениях. Касательные напряжения от поперечных сил достигают своего максимума Опасным является сечение в заделке, где одновременно имеют большое значение продольная и поперечная силы, изгибающий и крутящий моменты.
Рис. 11.5 Опасной точкой в этом сечении, будет точка, где σх и τху достигают значитель-ной величины (точка В). В этой точке действует наибольшее нормальное на-пряжение от изгиба Определив главные напряжения по формуле: σгл= находим σred= (при использовании критерия наибольших касательных напряжений m = 4, при использовании критерия удельной энергии изменения формы m = 3). Подставив выражения σα и τху, получаем:
σred=
или с учётом того, что Wр=2 Wz, A= σred= В случае, если вал испытывает изгиб в двух взаимно перпендикулярных плоскостях, то в формулу вместо Мz надо подставить Mtot= Приведенное напряжение σred не должно превышать допускаемого напряжения σadm, определённого при испытаниях при линейном напряжённом состоянии с учётом коэффициента запаса прочности. При заданных размерах и допускаемых напряжениях выполняют поверочный расчёт, Размеры необхо-димые для обеспечения безопасной прочности находят из условия Wz=
|
||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 136; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.164.22 (0.01 с.) |

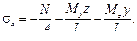
 Применив метод сечений, обнаружим в любом поперечном сечении продольную силу N = – F и изгибающие моменты: Му= FzF и Mz = FyF. Таким образом, напряжения можно представить в другом виде:
Применив метод сечений, обнаружим в любом поперечном сечении продольную силу N = – F и изгибающие моменты: Му= FzF и Mz = FyF. Таким образом, напряжения можно представить в другом виде: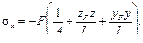
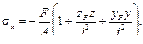
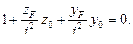
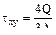 на оси бруса и незначительны для бруса сплошного сечения и ими можно пренебречь, по сравнению с касательными напряжениями от кручения, достигающих своего максимума
на оси бруса и незначительны для бруса сплошного сечения и ими можно пренебречь, по сравнению с касательными напряжениями от кручения, достигающих своего максимума 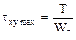 в периферийных точках (точка В).
в периферийных точках (точка В).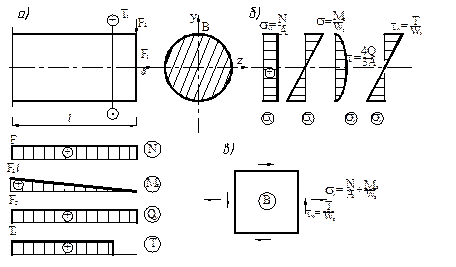
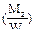 и касательное напряжение от кручения
и касательное напряжение от кручения 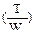 , а также нормальное напряжение от растяжения
, а также нормальное напряжение от растяжения 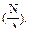
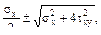
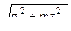
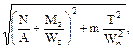
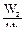 (см. 10.4),
(см. 10.4),