Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Чистый прямой изгиб призматического брусаСодержание книги
Поиск на нашем сайте
Задаются следующие условия: 1) волокна, параллельные оси бруса, испытывают равномерное растяжение или сжатие, переменное по высоте сечения; 2) деформации сдвига, касательные напряжения, поперечные силы и крутящий момент равны нулю; 3) сечения, плоские и нормальные к оси бруса до изгиба, остаются и после изгиба плоскими и нормальными к изогнутой оси бруса (гипотеза плоских сечений); следовательно, все волокна имеют общий взаимный угол поворота поперечных сечений и общий центр кривизны (рис.10.3); dv / dx = kx = const, хотя точные значения кривизны 1/ρ дуг концентрических окружностей неодинаковы; 4) физический закон − закон Гука для одноосного напряженного состояния; 5) из трех внутренних усилий, связанных с нормальными напряжениями, задана величина Mz; N = 0; My = 0. Для определения характеристик изогнутого бруса k х, ε х, σ х и u имеем следующие зависимости:
k х = d 2 v / dx 2, kx = –∂ ε х / ∂ y, σ х= E ε х. За основное неизвестное принимаем k х. Так как ε х – функция одной переменной у, то kx= – d ε х / dy. Следовательно,
Совместим границу между растянутыми и сжатыми волокнами (нейтральный слой) с координатной плоскостью у = 0, т.е. положим ε х = 0 при у = 0. В таком случае С = 0 и ε х = – kxy. Согласно физическому закону σ х = – Ekxy. В результате подстановки σ х в интегральные формулы для внутренних усилий получаем
В правой части третьей формулы принят плюс, так как в данном случае изгибающий момент и кривизна имеют одинаковые знаки. В первой формуле интеграл Во второй формуле интеграл Таким образом, определение оси z как главной центральной оси инерции сечения вносит ясность в расположение нейтрального слоя, который был совмещен с координатной плоскостью у = 0, и в ориентацию плоскости действия момента Mz, перпендикулярной оси z и естественным образом проходящей через вторую главную ось – у (признак прямого изгиба). Переписав третью интегральную формулу в виде Mz = EkxIz, где Iz – осевой момент инерции площади сечения, находим kx = Mz /(EIz). Окончательные выражения деформаций и напряжений имеют следующий вид: ε х = – (М z у)/(EIz), σ х = – (М z у)/ Iz. Минус поставлен для согласования знаков линейной деформации (напряжения) и изгибающего момента. При у > 0 положительному моменту соответствует отрицательное значение деформации (напряжения). Пренебрежение влиянием поперечных деформаций ε y = ε z = – v ε x на прогибы равносильно принятию для всех волокон прогибов, присущих нейтральному осевому волокну. Приравнивая правые части kx = d 2 v / dx 2и k х =М z /(EIz), получаем дифференциальное уравнение изогнутой оси бруса: d 2 v/dx 2 = М z /(EIz). Его интегралы:
При М z = const и Iz = const получаем
С 1, и С 2 находятся из граничных условий для v и
Анализ полученного решения приводит к следующим выводам: 1. Напряжения σ х не меняют своего закона по длине бруса и являются функцией только координаты у. На торцах на основании статического граничного условия они трансформируются в распределенную по закону пло-скости нагрузку Xp (рис.10.4), которая и соответствует Рис.10.4 рассмотренной деформации чистого изгиба. Независи-мость σ х от х справедлива при Iz = const. Таким образом, чистый изгиб возмо-жен лишь в случае призматического бруса. 2. Кривизна и деформация обратно пропорциональны величине Е Iz, называемой жесткостью при изгибе. Поперечный изгиб Силы, действующие перпендикулярно к оси бруса и расположенные в плос-кости, проходящей через эту ось, вызывают деформацию, называемую попереч-ным изгибом. Если плоскость действия упомянутых сил – главная плоскость, то имеет место прямой (плоский) поперечный изгиб. В противном случае изгиб называется косым поперечным. Брус, подверженный преимущественно изгибу, называется балкой 1. По существу поперечный изгиб есть сочетание чистого изгиба и сдвига. В связи с искривлением поперечных сечений из-за неравномерности распределе-ния сдвигов по высоте возникает вопрос о возможности применения формулы нормального напряжения σ х, выведенной для чистого изгиба на основании гипотезы плоских сечений.
. 1Однопролетная балка, имеющая по концам соответственно одну цилиндрическую неподвижную опору и одну цилиндрическую подвижную в направлении оси балки, называется простой. Балка с одним защемленным и другим свободным концом называется консолью. Простая балка, имеющая одну или две части, свешивающиеся за опору, называется консольной. Если, кроме того, сечения взяты далеко от мест приложения нагрузки (на расстоянии, не меньшем половины высоты сечения бруса), то можно, как и в случае чистого изгиба, считать, что волокна не оказывают давления друг на друга. Значит, каждое волокно испытывает одноосное растяжение или сжатие. При действии распределенной нагрузки поперечные силы в двух смежных сечениях будут отличаться на величину, равную qdx. Поэтому искривления сечений будут также несколько отличаться. Кроме того, волокна будут оказывать давление друг на друга. Тщательное исследование вопроса показывает, что если длина бруса l достаточно велика по сравнению с его высотой h (l / h > 5), то и при распределенной нагрузке указанные факторы не оказывают существенного влияния на нормальные напряжения в поперечном сечении и потому в практических расчетах могут не учитываться. а б в
В сечениях под сосредоточенными грузами и вблизи них распределение σ х отклоняется от линейного закона. Это отклонение, носящее местный характер и не сопровождающееся увеличением наибольших напряжений (в крайних волокнах), на практике обычно не принимают во внимание. Таким образом, при поперечном изгибе (в плоскости ху) нормальные напряжения вычисляются по формуле σ х = – [ М z (x)/ Iz ] y. Если проведем два смежных сечения на участке бруса, свободном от нагрузки, то поперечная сила в обоих сечениях будет одинакова, а значит, одинаково и искривление сечений. При этом какой-либо отрезок волокна ab (рис.10.5) переместится в новое положение a ' b ', не претерпев дополнительного удлинения, и следовательно, не меняя величину нормального напряжения. Определим касательные напряжения в поперечном сечении через парные им напряжения, действующие в продольном сечении бруса. Выделим из бруса элемент длиной dx (рис. 10.7 а). Проведём горизонта-льное сечение на расстоянии у от нейтральной оси z, разделившее элемент на две части (рис. 10.7) и рассмотрим равновесие верхней части, имеющей основа-
Рис.10.7 ние шириной b. В соответствии с законом парности касательных напряжений, напряжения действующие в продольном сечении равны напряжениям, действующим в поперечном сечении. С учётом этого в предположении о том, что касательные напряжения в площадке b N*- (N*+dN*)+ откуда где: N*- равнодействующая нормальных сил σ N*= где: S N*= откуда dN*= Тогда можно записать: Эта формула была получена в XIX веке русским ученым и инженером Д.И. Журавским и носит его имя. И хотя эта формула приближенная, так как усредняет напряжение по ширине сечения, но полученные результаты расчета по ней, неплохо согласуются с экспериментальными данными. Для того, чтобы определить касательные напряжения в произвольной точке сечения отстоящей на расстоянии y от оси z следует: - определить из эпюры величину поперечной силы Q, действующей в сечении; - вычислить момент инерции Iz всего сечения; - провести через эту точку плоскость параллельную плоскости xz и определить ширину сечения b; - вычислить статический момент отсеченной площади S Определим в качестве примера касательные напряжения в прямоуголь-ном поперечном сечении (рис. 10.6, в). Статический момент относительно оси z части сечения выше линии 1-1, на которой определяется напряжения запишем в виде: S Он изменяется по закону квадратной параболы. Ширина сечения в для прямоугольного бруса постоянна, то параболическим будет и закон изменения касательных напряжений в сечении (рис.10.6, в). При y = Для балки круглого поперечного сечения на нейтральной оси имеем: τмах =1.33
|
||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 121; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.44.22 (0.011 с.) |

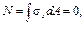
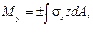
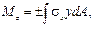
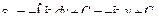
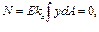
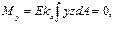
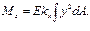
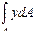 выражает статический момент площади сечения относительно оси z. Равенство его нулю свидетельствует о том, что ось z, в точках которой ε х = 0, проходит через центр тяжести сечения. Согласно физическому закону на этой оси σ х = 0. Следовательно, ось z есть линия нулевых напряжений при изгибе в плоскости ху. Она называется нейтральной осью сечения (нулевой линией). По обе стороны от нее нормальные напряжения имеют противоположные знаки и нарастают по единому линейному закону, образуя зоны растяжения и сжатия.
выражает статический момент площади сечения относительно оси z. Равенство его нулю свидетельствует о том, что ось z, в точках которой ε х = 0, проходит через центр тяжести сечения. Согласно физическому закону на этой оси σ х = 0. Следовательно, ось z есть линия нулевых напряжений при изгибе в плоскости ху. Она называется нейтральной осью сечения (нулевой линией). По обе стороны от нее нормальные напряжения имеют противоположные знаки и нарастают по единому линейному закону, образуя зоны растяжения и сжатия.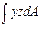 выражает центробежный момент инерции сечения относительно осей у и z. Равенство его нулю свидетельствует о том, что оси у и z – главные оси инерции сечения.
выражает центробежный момент инерции сечения относительно осей у и z. Равенство его нулю свидетельствует о том, что оси у и z – главные оси инерции сечения.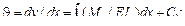
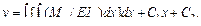
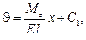
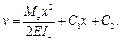
 .
. Следует обратить внимание на то, что волокно изгибается по параболе, а не по дуге окружности. Такой результат согласуется с исходным условием и является следствием использования не точного, а приближенного выражения кривизны изгиба.
Следует обратить внимание на то, что волокно изгибается по параболе, а не по дуге окружности. Такой результат согласуется с исходным условием и является следствием использования не точного, а приближенного выражения кривизны изгиба.
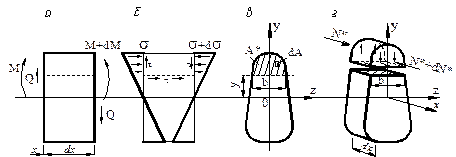
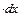 распределены равномерно ис-пользуем условие ΣХ = 0, получим:
распределены равномерно ис-пользуем условие ΣХ = 0, получим: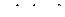
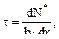
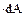 в левом поперечном сече-нии элемента dx в пределах “отсечённой” площадки А* (рис. 10.7 г):
в левом поперечном сече-нии элемента dx в пределах “отсечённой” площадки А* (рис. 10.7 г):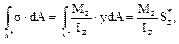
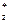 =
= 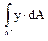 - статический момент “отсечённой” части поперечного сече-ния (заштрихованная площадь на рис. 10.7 в). Следовательно, можно записать:
- статический момент “отсечённой” части поперечного сече-ния (заштрихованная площадь на рис. 10.7 в). Следовательно, можно записать: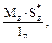
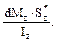
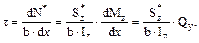
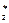 относительно главной центральной оси z и подставить найденные величины в формулу Жура-вского.
относительно главной центральной оси z и подставить найденные величины в формулу Жура-вского. 
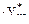 =b
=b 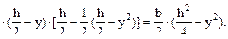
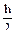 и у = −
и у = −