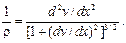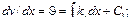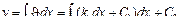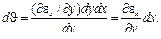Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поверочные и проектные расчетыСодержание книги
Поиск на нашем сайте
Условие безопасной прочности при кручении имеет вид τмах = T / Wp ≤ τ adm. Касательные напряжения действуют не только в поперечных сечениях бруса, но и в продольных, образуя двухосное напряженное состояние – чистый сдвиг. Он не будет однородным, поскольку величина В наклонных же сечениях стержня действуют нормальные и касательные напряжения. Наибольший интерес представляют главные напряжения σ1 = σmax = τ и σ3 = σmin = – τ с углом наклона площадок к оси бруса 45º и 135º. Опыты показывают, что хрупкие материалы при кручении разрушаются по винтовой поверхности, наклоненной к оси вала под углом 45º. Именно перпендикулярно этой поверхности действуют наибольшие растягивающие напряжения. Как видно из сказанного, помимо выполнения основного условия прочности, требуется обращать внимание на дополнительные проверки безопасности напряженного состояния. При заданных величинах τ adm и размерах сечения допускаемый крутящий момент равен Tadm ≤ τ adm WP. Для подбора сечения из условия прочности используется зависимость WP ≥ T /τ adm. Для круглого поперечного сечения WP = (π r 3)/2 = (π d)3/16 ≈ 0,2 d 3, поэтому можно определить непосредственно минимальный диаметр сечения:
Эпюра τ при кручении показывает, что материал бруса рационально используется только в периферийной зоне. Поэтому можно получить значительную экономию материала, удаляя слабо напряженную внутреннюю часть, т.е. изготовляя вал полым. Однако практически это возможно лишь до известного предела, поскольку чрезмерно тонкие стенки неустойчивы. Момент сопротивления трубчатого вала равен
Определение наружного В тонкостенной трубе практически во всех точках стенки возникают одинаковые напряжения, т.е. в этом случае напряженное состояние будет практически однородным. Вот почему опыты с кручением таких труб используют обычно для изучения чистого сдвига и, в частности, для установления предела текучести при сдвиге. При совмещении кручения с другими деформациями проверка прочности ведется по приведенному напряжению: σ red ≤ σ adm. При проектировании валов размеры их сечений назначаются так, чтобы не только удовлетворялось условие прочности, но и обеспечивалась в целях нормальной эксплуатации достаточно малая кривизна кручения. Условие жесткости имеет вид kt = T /(GIP) ≤ kt adm (рад/м), где kt adm – допускаемая кривизна кручения в радианах на единицу длины вала, или
где kt adm задается в градусах на единицу длины вала(допускаемый относитель-ный угол закручивания). Величина kt adm устанавливается техническими условиями. Для разных конструкций и для различных режимов работы вала она колеблется в доволь-но широких пределах: kt adm = (0,26...3,5)10-2 рад/м, или kt adm = (0,15...2,0) град/м. Допускаемый крутящий момент из условия жесткости для сплошного вала равен Tadm ≤ GIPkt adm, или Tadm ≤ (π GIPkt adm)/180. Диаметр вала вычисляется по формулам: а) в случае сплошного сечения
б) в случае кольцевого сечения
или
Модуль сдвига в случае сплошного вала определяется по формуле G ≥ T / (IPkt adm), или G ≥ (180 T)/ (π IPkt adm). Из проектных расчетов по условиям прочности и жесткости берутся наибольшие значения d и G и наименьшая величина Т adm. Диаметр округляется до ближайшей большей стандартной величины.
9.4 Практикум Примеры 1.На участке сплошного круглого вала D=10см действует крутящий момент Т=8 кHм. Проверить прочность и жёсткость вала, если τadm=50 МПа, Кt adm=0.5 Решение. Условие безопасной прочности
Kt= Выразив Kt в размерности Kt=1.02 что превышает величину допускаемого относительного угла закручивания Kt adm=0.5 τмax=40.75МПа < 50МПа, а жёсткость не обеспечена.
2. Стальной вал кольцевого сечения D=10см, d=8см. нагружен моментом, вызвавшим τмах=τadm=70МПа. Что произойдёт, если этот вал заменить сплош-ным круглым валом диаметром 8см. (материал сохранён). Решение. Максимальные касательные напряжения в вале Для кольцевого сечения Wр= τ 3. Для сплошного овала (задача №2) определить появились ли пласти-ческие деформации, если известно, что nadm=1.8? Решение. Для пластичных материалов nadm= τу =70 Действующие напряжения превысили предел текучести, следовательно появились пластические деформации.
Вопросы для повторения 1. Когда в брусе возникают деформации кручения? 2. Как определяют величину крутящего момента, действующего в сече-нии? 3. Какое правило знаков для Т принято при построении эпюр? 4. Как строятся эпюры крутящих моментов? 5. Как определяют угол закручивания на участке вала? 6. Что называют относительным углом закручивания θ (или кривизной кручения kt)? 7. Какие напряжения возникают в поперечном сечении круглого вала при кручении и как они направлены? 8. Какое напряженное состояние возникает в каждой точке вала круглого сечения при кручении? 9. Что называется жесткостью сечения при кручении? 10. Что выражает условие жесткости при кручении? 11. Чем объясняется, что вал кольцевого сечения при кручении экономичнее вала сплошного сечения? 12. Как выполняют расчет вала на прочность? 13. Каким следует проектировать вал, если величины крутящих момен--тов существенно отличаются на его участках? 14. Равен ли полярный момент сопротивления кольцевого сечения раз-ности полярных моментов сопротивления наружного и внутреннего кругов?
Тесты для повторения 1. Касательные напряжения в поперечном сечении вала направлены: (а) к оси вала; (б) перпендикулярно плоскости действия Т; (в) вдоль образующей; (г) перпендикулярно радиусу сечения. Ответ: (г), поскольку б и в не соответствуют формулировке задания и только касательные напряжения, перпендикулярные радиусу создают крутящие мо-менты относительно оси вала.
2. Полярный момент сопротивления Wр определяется как: (а) Ответ: (б), поскольку Wp- геометрическая характеристика плоского сечения, имеющая размерность см3, м3.
3. Наибольшее касательное напряжение при кручении определяеися по формуле: (а) Ответ: (а), поскольку б позволяет определить τ в любой точке сечения вала и только при ρ = ρмах позволит вычислить максимальные τ.
4. Какая из указанных на рисунке площадок (1 и 2 наклонены к оси под углом 45
(а) хрупкого материала;
(б) пластичного материала;
(в) анизотропного (дерево).
Ответы: - в площадке 1 действует σ1 - наибольшее главное растягивающее напряжение, а хрупкие материалы имеют прочность на растяжение минималь-ную (а) - 1;
- в площадках 4 и 3 действуют равные по величине касательные напряжения, но пластичный материал имеет прочность на срез, составляющую от прочности на растяжение только 50-60%, поэтому (б) - 4;
- деревянный вал имеет наименьшую прочность вдоль волокон и разрушается по площадке 3, т.о. (в) - 3.
5. Какое из выражений соответствует величине полярного момента инерции, если С равно отношению внутреннего диаметра кольца к внешнему:
(а)
Ответ: (в), поскольку размерность Јр-см4, а из двух ответов, удовлетворяющих этому требованию только (в) верен.
Контрольные тесты
1. При кручении в поперечных сечениях стержня возникает внутреннее уси- лие … 2. Величина касательного напряжения в любой точке поперечного сечения определяется по формуле… 3. Величина наибольшего касательного напряжения в поперечном сечении равна… 4. Полярный момент сопротивления сплошного круглого вала определяется по формуле… 5. Касательные напряжения в точках на оси скручиваемого стержня равны… 6. При кручении в поперечных сечениях вала возникают … деформации. 7. Диаметр вала сплошного сечения при кручении, определяемый из условия прочности, должен быть не менее … 8. Жесткостью сечения вала называют произведение … 9. Главные площадки при кручении ориентированы относительно поперечного сечения под углом α, равным … 10. Величина главных напряжений при кручении равна … 11. Диаметр вала сплошного сечения, определяемый из условия жесткости при кручении, не должен быть менее величины … 12. Полярный момент сопротивления вала кольцевого сечения равен … 13. Относительный угол закручивания (кривизна кручения) определяется выражением … 14. Брус кольцевого сечения более рационален, чем сплошной круглый брус потому, что … 15. Условие жесткости при кручении имеет вид … 16. Угол закручивания вала на участке определяют по формуле … 17. Угол закручивания вала будет тем больше, чем … будет его жесткость. 18. В качестве вала использовать чрезмерно тонкостенную трубу невозможно, потому что … 19. Если известны материал и диаметр сплошного вала, то величина допускаемого крутящего момента не должна превышать … 20. Если диаметр вала подобран и из условия безопасной прочности и из условия обеспечения жесткости, то необходимо назначить (больший?, мень-ший?) из полученных размеров?
ИЗГИБ
Плоский изгиб волокна
При малых перемещениях длина хорды волокна l 1 мало Рис. 10.1 отличается от первоначальной длины волокна l. Поэтому можно принять l 1= l, т.е. пренебречь продольными перемещениями u (рис.10.1, б). В то же время длина искривленного волокна считается равной длине первоначального прямолинейного волокна. В пределах малых перемещений допустимо считать Поперечные сечения волокна сохраняют прямые углы с касательными к оси волокна после его деформирования. Поэтому углы kxm = ∆ При малых углах поворота (∆ s ≈ ∆ x) kxm = ∆ Устремляя ∆ s и ∆ x к нулю, в пределе получаем kx = d (точное и приближенное значения кривизны изгиба в точке). Очевидно, что
Имеется другое определение кривизны: kx = 1 / ρ – 1 / r 0, где r 0(ρ) – радиус кривизны до (после) деформирования волокна. Для прямого волокна r 0 = ∞ и kx = 1/ρ. Из дифференциальной геометрии известно, что
При малых углах поворота ( 1/ρ ≈ d 2 v / dx 2. Итак, формула kx = d 2 v / dx 2 дает приближенное значение кривизны при изгибе. Величины v,
или
C 1 и C 2 находятся из граничных условий для прогибов и углов поворота. Их смысл легко обнаружить, если положить kx = 0. Тогда С 2 + C 1 x – уравнение прямой линии, в котором С 2 – поперечное поступательное перемещение линии, а С 1 – ее поворот. Установим связь между характеристиками изгиба волокна и компонентами деформации в точке. Рассмотрим изгиб волокна, параллельного оси х, с бесконечно малым поперечным сечением dz x dy (рис. 10.2). Пусть в точке С линейная деформация равна ε x, а в точке А – ε x +(∂ ε x / ∂у) d у.
Рис.10.2 Рис.10.3 Взаимный поворот линейных элементов АС и BD равен
Кривизна волокна
Знак минус поставлен для согласования положительной кривизны и отрицательной производной ∂ ε x / ∂ y.
|
|||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 157; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.192.248 (0.012 с.) |

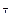 изменяется по радиусу поперечного сечения. Касательные напряжения в продольных сечениях могут быть причиной разрушения анизотропного материала. Древесина, как известно, имеет сравнительно низкую прочность на скалывание вдоль волокон. Поэтому разрушение деревянного образца при кручении начинается с образования продольных трещин.
изменяется по радиусу поперечного сечения. Касательные напряжения в продольных сечениях могут быть причиной разрушения анизотропного материала. Древесина, как известно, имеет сравнительно низкую прочность на скалывание вдоль волокон. Поэтому разрушение деревянного образца при кручении начинается с образования продольных трещин.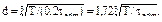
 .
.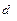 и внутреннего
и внутреннего 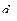 диаметров сечения ведется методом последовательных попыток (либо задаются их соотношением).
диаметров сечения ведется методом последовательных попыток (либо задаются их соотношением).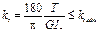 (град/м),
(град/м),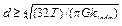 или
или 
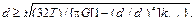
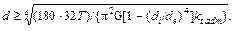
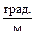 и модуль сдвига G=0.8
и модуль сдвига G=0.8 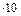 5МПа.
5МПа.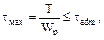 где Wp=
где Wp=  =196 см3,
=196 см3,  что меньше τadm.
что меньше τadm. =1.02
=1.02 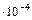
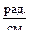 .
.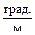 , получим
, получим =0.58
=0.58 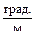 на 16%. Следовательно – прочность вала обеспечена
на 16%. Следовательно – прочность вала обеспечена .
. , а для вала сплошного сечения Wр=
, а для вала сплошного сечения Wр=  . По условию для вала кольцевого сечения τмах=70 МПа, очевидно, что для вала сплошного сечения максимальные напряжения будут больше во столько раз, во сколько его момент сопротивле-ния меньше.
. По условию для вала кольцевого сечения τмах=70 МПа, очевидно, что для вала сплошного сечения максимальные напряжения будут больше во столько раз, во сколько его момент сопротивле-ния меньше. =τ
=τ 
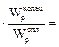 70
70 
 , следовательно
, следовательно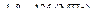 .
.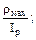 (б)
(б)  (в)
(в) 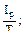 (г)
(г) 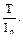
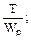 (б)
(б)  (в)
(в) 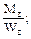 (г)
(г) 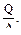
 ) является опасной для:
) является опасной для:
 (б)
(б)  (в)
(в) 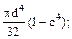 (г)
(г) 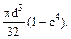
 Рассмотрим волокно ab, параллельное оси х. В результате изгиба прямое волокно искривляется (рис.10.1, а). Изгиб волокна сопровождается попереч-ными перемещениями (прогиба-ми) v и углами поворота (девиа-циями)
Рассмотрим волокно ab, параллельное оси х. В результате изгиба прямое волокно искривляется (рис.10.1, а). Изгиб волокна сопровождается попереч-ными перемещениями (прогиба-ми) v и углами поворота (девиа-циями) 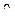 его линейных элемен-тов. Углы
его линейных элемен-тов. Углы 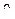 характеризуют в то же время повороты поперечных сечений. Вследствие их неодинаковости образуются взаимные повороты с углами
характеризуют в то же время повороты поперечных сечений. Вследствие их неодинаковости образуются взаимные повороты с углами 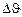 . Отношение
. Отношение  .
.