
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диаграммы сжатия. Особенности разрушения при сжатии
Испытание металлов на сжатие производится на образцах в виде цилиндров, высота которых равна диаметру (обычно 20 мм). Для более длинных образцов в опытах трудно избежать искривления. Другие материалы испытываются, как правило, на образцах в виде кубиков. Ребра кубиков принимаются обычно равными: 50 мм для дерева, 70 мм для цемента, от 100 до 300 мм для бетона.
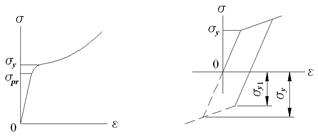
При сжатии цилиндрический образец из пластичного материала при напряжениях ниже σ р r или σ у ведет себя так же, как при растяжении. В дальнейшем появляются заметные остаточные деформации. Трение между опорными плитами пресса и основаниями образца препятствует поперечным деформациям материала у торцов образца; он принимает бочкообразную форму.1 По мере увеличения площади поперечного сечения приходится для дальнейшего деформирования увеличивать нагрузку, образец в конце концов расплющивается. Напряжения, аналогичного σ u при растяжении, наблюдать не приходится. Диаграмма сжатия для малоуглеродистой стали показана на рис. 5.4. Диаграмма истинных напряжений располагается несколько ниже (начиная от площадки текучести). Рис. 5.4 Рис. 5.5
Материал, испытывающий деформации противоположного знака после наклепа, имеет меньшие величины σ р r, σ e, σ y. Это явление носит название эф-фекта Баушингера (по имени ученого, впервые его описавшего). Его графичес- . 1Для уменьшения трения образцы иногда смазывают жиром или парафином или же заменяют плоские плиты пресса коническими с углом наклона образующей конуса, равным углу трения. кое отражение дано на рис. 5.5 на примере упрощенной диаграммы (σ y 1 < σ y). Иной характер деформирования наблюдается у хрупких материалов. Их диаграммы сжатия представляют собой слабо искривленные линии. Величина разрушающей нагрузки значительно большая, чем в случае растяжения образца той же площади сечения. На характер разрушения образца из камня, бетона и других материалов такого рода влияет трение между плитами пресса и образцом. При его наличии происходит выкалывание материала с боков, а при его отсутствии – продольное растрескивание. При одинаковых поперечных сечениях призматический образец разрушится при меньшей нагрузке, чем образец в форме куба. В связи с этим говорят о призменной и кубиковой прочности, понимая под последней напряжения, при которых происходит разрушение образца.
Прочность меняется в зависимости от размеров кубика, уменьшаясь при их увеличении. Все же эта зависимость имеет асимптотический характер, т.е. при определенных размерах прочность стабилизируется. Таким образом, прочность образца хотя и не вполне отражает прочность материала, работающего в конструкции, но позволяет провести сопоставление свойств различных материалов. Чугунный образец при сжатии разрушается в результате образования наклонных трещин, направленных примерно под углом 45° к оси образца, т.е. параллельно площадкам, на которых возникают наибольшие касательные напряжения.
Соотношения упругости В двух предыдущих главах рассматривались закономерности напряженного и деформированного состояний, отражающих две стороны одного и того же явления. Результаты механических испытаний материалов составляют основу физических уравнений, устанавливающих связь между напряжениями и деформациями. Напряжения в упругом теле образуют физическое силовое поле, которое можно охарактеризовать некоторой потенциальной функцией (потенциалом), позволяющей выразить компоненты напряжения в виде производных. Опыты показали, что для создания напряженного состояния необходимо затратить энергию, которая переходит во внутреннюю механическую энергию. Ее накопление связывают с работой внутренних сил. На бесконечно малом этапе деформирования с приращениями дение постоянной силы на путь с точностью до бесконечно малых второго порядка. Выделим из тела бесконечно малый параллелепипед с ребрами dx, dy, dz. Бесконечно малым площадкам можно приписывать постоянные напряжения и перемещения. Работа внутренних продольных сил, которым соответствуют напряжения σ x (рис. 5.6, а или рис. 5.6, б), вычисляется как произведение силы σ х dydz на перемещение d ε xdx т.е. σ х d ε xdxdydz. Аналогично вычисляется работа двух других продольных сил: σ y d ε ydxdydz, σ z d ε zdxdydz.
Работа внутренних сдвигающих сил, которым соответствуют напряжения τ ху (рис. 5.7, а или 5.7, б), вычисляется как произведение силы τ ху dydz на перемеще-ния d γ xydx, т.е. τ ху d γ xydxdydz. Аналогично вычисляется работа двух других сдвигающих сил: τ yz d γ yzdxdydz, τ zx d γ zxdxdydz. Элементарная удельная работа внутренних сил d ũ (работа на бесконечно малом этапе деформирования, приходящаяся на единицу объема) есть сумма полученных величин работ, разделенная на объем бесконечно малого параллелепипеда dxdydz:
а а
Рис. 5.6 Рис. 5.7
В упругом теле удельная работа внутренних сил не зависит от пути дости-жения того или иного деформированного состояния, а является функцией лишь окончательных значений деформации: ũ=ũ (ε x,ε y,ε z,γ xy,γ yz,γ zx).
Приращение этой функции с точностью до бесконечно малых второго порядка можно заменить ее полным дифференциалом:
Сравнивая два выражения для d ũ и учитывая независимость приращений деформаций, получаем соотношения:
которые позволяют считать ũ потенциалом. Эти соотношения называются формулами Грина (по имени английского ученого, впервые их получившего). Они применимы как для линейно-, так и для нелинейно-упругого тела при малых деформациях. Предполагалось, что в недеформированном состоянии напряжения равны нулю. После снятия нагрузки тело приходит в свое естественное недеформированное состояние и, следовательно, восстанавливает свою первоначальную форму. Происходит это за счет накопленной данным материалом потенциальной энергии деформации, численно равной работе внутренних сил. Вследствие этого удельная потенциальная энергия деформации ū также должна рассматриваться как упругий потенциал поля напряжений. Следовательно,
Введем в рассмотрение удельную дополнительную энергию (энергию напряжений), элементарная вели-чина которой
В геометрическом смысле энергия Рис. 5.8 дополнением энергии Приращение этой функции можно заменить ее полным дифференциалом:
Соотношения
называются формулами Кастильяно. Линейный физический закон
В упругом анизотропном теле каждый из компонентов напряжений может зависеть от всех составляющих деформаций:
……………………………
Ограничиваясь малыми деформациями, связь между напряжениями и деформациями можно принять линейной:
…………………………………………..
где А 11, А 12,…, А 66 – жесткости линейно-упругого состояния тела (упругие жесткости). Эти зависимости называются уравнениями обобщенного закона Гука в прямой форме. Прообразом является физический закон, обнаруженный Р. Гуком из опыта при одноосном напряженном состоянии тела. Обратные соотношения имеют вид
…………………………………………..
где B 11, В 12,…, B 66 – податливости линейно-упругого состояния тела (упругие податливости). Чем больше А ij, тем (при неизменности деформаций) бóльшими будут напряжения, т.е. тем жестче тело. Чем больше В ij, тем (при неизменности напряжений) бóльшими будут деформации, т.е. тем податливее тело. Обобщенный закон Гука можно представить в матричной форме:
где
Матрица D называется матрицей упругих жесткостей (матрицей упругости). Обратная матрица D -1 по смыслу является матрицей упругих податливостей. Поскольку упругому телу присущи обратимые процессы деформирования, то при использовании потенциальной функции напряжений можно обнаружить, что А ij = А ji. Следовательно, коэффициенты, расположенные симметрично относительно главной диагонали матрицы, попарно равны между собой. Тогда в анизотропном теле число упругих постоянных оказывается равным 21. Предположим, что одна из координатных плоскостей, например, плоскость хОу, является плоскостью симметрии упругих свойств. Тогда следует заменить τ xz и τ yz на (–τ xz) и (–τ yz) соответственно, а γ xz и γ yz – на (–γ xz) и (–γ yz). При неизменности физических соотношений ряд коэффициентов обращается в нуль: A 15 = A 16 = A 25 = A 26 = A 35 = A 36 = A 45 = A 46 = 0. Так, число упругих постоянных при наличии только одной плоскости симметрии сокращается до 13. В случае, если через каждую точку тела проходят три ортогональные плоскости симметрии упругих свойств (ортотропное тело), число независимых постоянных снижается до 9 (А 14 = А 24 = А 34 = А56= 0). Примерами ортотропных материалов служат дерево, фанера, железобетон, армированные пластики, холодный прокат черных металлов. В случае полной симметрии (изотропное тело), когда любая плоскость есть плоскость упругой симметрии, имеем следующие физические уравнения:
Упругие постоянные E, v и G взаимосвязаны. Это можно показать на примере вычисления деформации сдвига
при совмещении осей x и y с главными осями 1 и 2:
Имея в виду, что
Следовательно, изотропное тело имеет две упругие постоянные, в качестве которых можно принять, например, модуль продольной упругости Е и коэффициент Пуассона v. Величина G называется модулем сдвига. Запишем выражения для напряжений:
С учетом этих зависимостей вычислим удельную потенциальную энергию деформаций путем интегрирования
в пределах от 0 до ε x,… при
где:
Выразив деформации через напряжения, получим
По физическому смыслу упомянутое выше интегрирование сводится к вычислению площадей треугольников на линейном участке диаграммы "напряжение − деформация", ограниченном деформациями ε x,…,γ zx соответственно:
Следовательно, удельная потенциальная энергия деформации, накапливае-мая в упругом теле, равна полусумме произведений компонентов напряжений на соответствующие им компоненты деформации. Этот факт тесно связан с энергетической теоремой Клапейрона для линейно деформирующегося тела, в связи с чем соответствующую зависимость называют формулой Клапейрона. Введем величины Удельная потенциальная энергия изменения объема равна
или
Удельная потенциальная энергия изменения формы равна
или
Соотношения пластичности
При одноосном напряженном состоянии условие пластичности устанавли-вается опытным путем. В этом случае отлично от нуля только главное напря-жение σ1 и пластические деформации появляются при σ1 = σ y. При чистом сдвиге условие пластичности, получаемое также опытным путем, имеет вид τ = τ y, где τ y – предел текучести при чистом сдвиге. В случае плоского или объемного напряженного состояния при бесконечном множестве соотношений между компонентами напряжений очевидность наступления пластичности исчезает. Остается гипотетический путь с последующей экспериментальной проверкой. Появляющиеся с момента наступления текучести линии Людерса – Чернова согласуются с расположением наибольших деформаций сдвига. Это способ-ствовало утверждению критерия наибольших касательных напряжений и соот-ветствующего условия пластичности Треска – Сен-Венана: пластические деформации возникают, когда максимальные касательные напряжения дости-гают величины предела текучести при чистом сдвиге (τmax = τ у). Поскольку τmax = (σ1 –σ3) /2, то, подставляя сюда главные напряжения при одноосном напряженном состоянии (σ1=σ y, σ3 = 0), получаем τmax = σ y /2. Сравнивая эту формулу с условием пластичности τmax = τ у, заключаем, что τ y = σ y /2. Условие пластичности Треска – Сен-Венана принимает вид σ red = σ1 – σ3 =σ y, где: σ red – приведенное напряжение. Его следует понимать как напряжение в условиях одноосного напряженного состояния, эквивалентное по своему эффекту напряжениям при плоском или объемном напряженном состоянии. Связь напряженного состояния с накоплением потенциальной энергии деформации явилась предпосылкой энергетических критериев предельного состояния материала. Начало такого рода критериям положил в 1886г. итальянский ученый Э. Бельтрами, полагавший необходимость учета полной энергии деформации, что оказалось справедливым лишь при σ0 > 0.
В 1904 г. М. Губер предложил в качестве критерия предельного состояния материала удельную энергию изменения формы. Р. Мизес и Г.Генки приняли ее для формулировки условия пластичности: пластическое состояние материала наступает, когда удельная энергия изменения формы становится равной такого рода энергии при одноосном растяжении образца в момент достижения предела текучести. Выражение последней имеет вид
Следовательно, условие пластичности Губера – Мизеса – Генки имеет вид
или
По результатам оно достаточно близко к условию Треска-Сен-Венана. Эксперименты несколько лучше подтверждают условие Губера – Мизеса Ген-ки, которое, кроме того, менее громоздко с математической точки зрения (для определения τмax надо проводить исследование главных напряжений). 5.7 Практикум Вопросы для повторения 1. Чем отличается абсолютная продольная и относительная продольная деформации? 2. Какова размерность относительной деформации? 3. Назовите все характеристики прочности материала. Сколько их? 4. Назовите характеристики пластичности? 5. Какие материалы считаются хрупкими? Какие из механических хара-ктеристик выступают в качестве порогового критерия? 6. Что называется модулем продольной упругости Е? Как сказывается величина Е на деформации бруса? 7. Как формулируется закон Гука? 8. Напишите формулы для абсолютной и относительной продольной де-формации. 9. Что называют коэффициентом Пуассона и в каких пределах он прини-мает значения для различных материалов? 10. Какое явление называют “наклёпом” (нагартовкой)? 11. Чем отличается диаграмма растяжения малоуглеродистой стали от диаграммы для высокоуглеродистой стали? 12. Что называют упругостью, пластичностью, ползучестью? 13. Чем отличаются диаграммы растяжения и сжатия для пластичных ма-териалов? 14. Чем отличаются диаграммы растяжения и сжатия для хрупких материалов? 15. О чём свидетельствует появления на образце линий Людерса-Чернова? 16. Что называют обобщённым законом Гука? 17. Как записывается условие пластичности Треска-Сен-Венана? 18. Как записывают в главных напряжениях условие пластичности Губера-Мизеса-Генки? 19. Какие материалы называют анизотропными? 20. Как изменяются механические свойства материала с повышением и по- нижением температуры?
Тесты для повторения
1. Машинная диаграмма выражает зависимость: (а) σ ~ ε; (б) σ ~ Ответ: (г), поскольку диаграммный аппарат машины фиксирует зависимость абсолютного удлинения
2. Всегда ли напряжения, определяемые делением силы на начальную площадь, являются “истинными”? (а) всегда; (б) только в зоне текучести; (в) только в зоне упрочнения; (г) только в зоне малых упругих деформаций. Ответ: (г), поскольку только при малых упругих деформациях изменение пло- щади пренебрежимо мало.
3. Для каких материалов не следует вычислять условный предел текучести σ 0.2? (а) для всех пластичных; (б) для хрупких; (в) для пластичных материалов имеющих площадку текучести; (г) для всех материалов. Ответ: (в), поскольку при наличии площадки текучести определяется физический предел текучести σу, в других же случаях определяют условный предел текучести – напряжение при котором относительная деформация составляет 0.2%.
4. При растяжении материал был нагружен таким образом, что произошло его упрочнение. Как изменились его свойства? (а) увеличилась величина σ u; (б) увеличился σ рr, а δ уменьшилось; (в) увеличились прочностные и пластические характеристики; (г) увеличились σ рr и δ. Ответ: (в), поскольку попав в зону упрочнения материал при повторном нагружении уже не фиксирует площадку текучести, его предел упругости по-высился до уровня напряжений “упрочнения”, однако его характеристики пластичности ухудшились.
5.Какая из механических характеристик отличается при испытании нормаль-ных и коротких (l =5d) образцов? (а) σе; (б) ψ; (в) σ u; (г) δ. Ответ: (г), поскольку зона местной текучести (образование утяжины перед разрывом) имеет примерно одинаковые размеры для любого образца, то отно-сительное удлинение δ у пятикратных (коротких) образцов получается более высоким.
6. Для свойств хрупкого материала характерна следующая зависимость (р -ра-стяжение, с - сжатие); (а) σuр > σuс; (б) σур < σус; (в) σuр < σuс; (г) σур > σус. Ответ: (в), поскольку для хрупких материалов временноt сопротивление на сжатие существенно выше.
Контрольные тесты
1. Рабочая длина нормального образца больше его диаметра в: (а) в 5 раз; (б) в 10 раз; (в) в 2 раза; (г) в 7 раз.
2. В пределах малых упругих деформаций полная деформация равна: (а) сумме упругой и пластической; (б) разности пластической и упругой; (в) упругой; (г) пластической.
3. В зоне упрочнения полная деформация равна: (а) упругой; (б) пластической (в) сумме упругой и пластической; (г) разности пластической и упругой.
4. Какой из вариантов соотношения характеристик прочности является вер-ным? (а) σu > σрr > σу > σе; (а) σpr > σе > σу > σu; (а) σu > σpr > σе > σу; (а) σu > σу > σе > σpr.
5. Если модуль продольной упругости первого материала Е 1> Е 2 – модуля вто-рого, то при одинаковых напряжениях в первом и втором материалах относи-тельные продольные деформации: (а) ε1
6. Отличаются ли модули продольной упругости материала при сжатии и при его растяжении? (а) не отличаются; (б) Eсж > Eраст; (в) отличаются незначительно; (г) Eсж < Eраст.
7. Равенство нулю коэффициента Пуассона (ν =0) свидетельствует о том, что: (а) отсутствуют относительные продольные деформации; (б) при наличии относительных продольных отсутствуют относительные попе-речные деформации; (в) тело не нагружено; (г) материал имеет очень низкий модуль продольной упругости.
8. Для хрупкого материала отношение временных пределов прочности при сжатии и при растяжении: (а) равно 1; (б) >1; (в) <1; (г) >>1.
|
||||||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 226; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.39.23 (0.108 с.) |
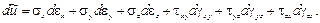

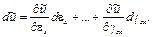
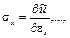


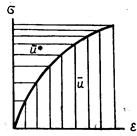 Потенциал линейной теории деформирования представляется многочленом второй степени. Потенциал поля напряжений, представленный многочленом третьей степени по инвариантам тензора дефор-маций, соответствует квадратичной форме физичес-кого закона, т.е. физической нелинейности низшего порядка.
Потенциал линейной теории деформирования представляется многочленом второй степени. Потенциал поля напряжений, представленный многочленом третьей степени по инвариантам тензора дефор-маций, соответствует квадратичной форме физичес-кого закона, т.е. физической нелинейности низшего порядка.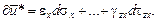
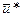 является
является 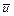 , поскольку вместе они составляют прямоугольник, изображенный на рис. 5.8. При линейном физическом законе
, поскольку вместе они составляют прямоугольник, изображенный на рис. 5.8. При линейном физическом законе 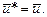
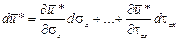 .
.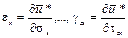

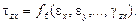
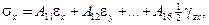
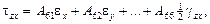
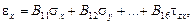
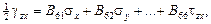

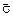 – тензор напряжений;
– тензор напряжений;  – тензор деформаций;
– тензор деформаций;
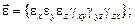
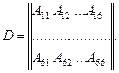
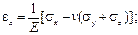

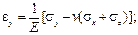
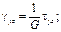



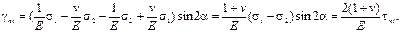
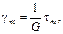 получаем
получаем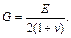

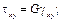
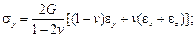
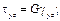
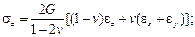
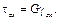

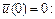

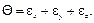
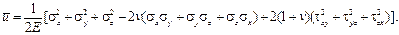
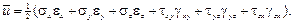
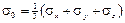 и
и 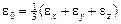 и предста-вим рассматриваемую энергию в виде двух составляющих.
и предста-вим рассматриваемую энергию в виде двух составляющих.

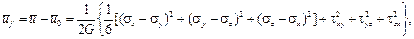
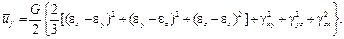
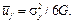
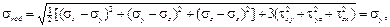

 l; (в) F ~ ε; (г) F ~
l; (в) F ~ ε; (г) F ~ 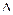 l от величины силы F в каждый момент нагружения.
l от величины силы F в каждый момент нагружения.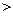 ε2; (б) ε1 = ε2; (в) ε1
ε2; (б) ε1 = ε2; (в) ε1 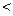 ε2; (г) ε1 < ε2.
ε2; (г) ε1 < ε2.


