
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моменты инерции простейших фигур
Прямоугольник. Определяя элементарную площадь dA в виде произведе-ния bdy или hdz (рис.3.2, а,в), вычисление
Момент инерции параллелограмма (рис.3.2, б) относительно центральной оси z, параллельной основанию b, определяется также по формуле
а б в Рис. 3.2 Это следует из того, что момент инерции фигуры не меняется от перемеще-ния ее частей параллельно той оси, относительно которой определяется эта характеристика (а именно так из прямоугольника образован параллелограмм). Однако момент инерции параллелограмма относительно оси у нельзя вы-числить по формуле для прямоугольника, так как в этом случае элементарные площадки сдвинуты непараллельно оси у.
Следовательно, Рис. 3.3
Круг. Вычислим полярный момент инерции круга радиусом r (рис.3.4). Элементарная площадь, вырезанная двумя радиусами и двумя окружностями, равна dA = ρ d φ d ρ. Интегрирование по всей площади заменяется двойным интегрированием:
Моменты инерции кольца находим как разность моментов инерции двух кругов – наружного (радиус re) и внутреннего (радиус ri):
Рис.3.4 Зависимости между моментами инерции относительно Параллельных осей
При известных величинах моментов инерции относительно осей z и у опре- делим моменты инерции относительно других осей z 1 и y 1, параллельных задан-ным (рис.3.5). Пользуясь общей формулой для осевых моментов инерции, находим
Если оси z и y центральные, то
Из полученных формул видно, что моменты инерции относительно центральных осей (когда
Рис. 3.5
3.4 Главные оси и главные моменты инерции сечения
Исследуем изменение моментов инерции при повороте осей координат. При известных величинах моментов инерции относительно осей z и у (не обязательно центральных) определим моменты инерции относительно осей z 1 и y 1, повернутых относительно заданных на угол α (рис.3.6). Координаты площади dA в осях z 1, y 1 выражаются че рез координаты z, у следующим образом: Рис. 3.6
z 1 = OC + CD = OC + AE = z cosα + y sinα;
y1 = BE – DE = BE – CA = y cosα – z sinα. Подставим эти значения в исходные выражения моментов инерции:
Уяснив смысл интегралов, окончательно находим
С изменением угла поворота осей координат α каждый из моментов инерции Iz и Iy меняется, а сумма их, равная Ip, остается неизменной. Очевидно, существует такое значение α0, при котором один из моментов инерции достигает своего максимального значения, в то время как другой принимает минимальное значение. Для определения экстремума приравняем нулю первую производную от Iz 1 и положим α = α0:
или
Выражение в левой части представляет собой не что иное, как tg Поскольку формула дает два значения угла α0′ иα0″ = α0′+90º, то существуют две взаимно перпендикулярные главные оси. Соответствующие им моменты инерции называют главными моментами инерции сечения. Ось максимума всегда составляет меньший угол (α0′) с той из осей (z или у), относительно которой осевой момент инерции имеет большее значение. Напомним, что положительные углы откладываются от оси z против хода часовой стрелки.
Для определения главных моментов инерции отразим значение углаα0 в выражении
После несложных преобразований получим
Эта формула позволяет вычислить главные моменты инерции, не определяя положение самих главных осей.
сил. Для прокатных профилей положение глав-ных осей и величины главных центральных момен-тов инерции даны в таблицах сортамента. Рис.3.7 Практикум Примеры 1. Определить положение главных центральных осей и величину главных центральных моментов инерции для составного сечения (рис.3.8). Построить эллипс инерции. Решение. Центр тяжести фигуры лежит на оси симметрии у, которая и является главной центральной осью. Выбираем произвольную ось z ' и определяем ординату центра тяжести, предварительно разбив сечение на два прямоугольника: Через точку С перпендикулярно оси у проводим ось z, которая и будет другой главной центральной осью.
Рис. 3.8
Для каждого из прямоугольников находим моменты инерции относительно их главных центральных осей:
а также расстояния их центров тяжести от оси z:
Используя зависимости между моментами инерции относительно парал-лельных осей, находим величины главных центральных моментов инерции:
Определяем радиусы инерции:
и строим эллипс инерции (см.рис.3.8), отложив величины iz и iy на перпендику-лярах к соответствующим осям. 2. Найти расстояние с между ветвями составного стержня, обеспечивающее равенство главных моментов инерции сечения (рис.3.9). Решение. Требуемое условие обеспечивается равенством моментов инерции относительно осей симметрии z и у, являющихся главными центральными осями сечения. Разбиваем каждую часть сечения на три прямоугольника, как показано на рис.3.9, и определяем моменты инерции:

Приравнивая Iy и Iz, получаем уравнение
или
откуда с = 4,19 см. Здесь и отрицательный корень с = –13,73 см имеет смысл. Читателю предлагается изобразить составное сечение для этого случая.
Вопросы для повторения
4. Что называют осевыми, центробежными, полярными моментами инерции сечения?
6. Чему равна сумма осевых моментов инерции сечения относительно двух взаимно перпендикулярных осей?
9. Что такое главные центральные оси инерции и почему необходимо вы-числять значения главных моментов инерции относительно главных централь-ных осей? 10. Как определяют главные моменты инерции и положение главных осей? 11. Чему равен центробежный момент инерции относительно главных осей инерции? 12. Какие центральные оси являются главными у сечений, имеющих более двух осей симметрии? 13. Почему производят разбивку сложного сечения на составляющие простые части при определении статических моментов и моментов инерции сечения?
Тесты для повторения 1. Статический момент площади сечения относительно центральной оси “Υ” (а) Sy > 0; (б) Sy < 0; (в) Sy = 0; (г) Sy Ответ: (в), потому что признаком того, что из семейства параллельных осей ось, относительно которой статический момент равен нулю, является цент-ральной.
(а) – у; (б) - х1; (в) - х2; (г) -х3. Ответ: (г) так как Sх
3. Если Jy=Jz, а D yz=0, то оси “y”,”z” являются:
(а) центральными; (б) главными центральными; (в) осями симметрии; (г) главными. Ответ: (г), потому что равенство центробежного момента инерции нулю – необходимое и достаточное условие для главных осей инер-ции. Если оси “y”,”z” были бы центральными, то необходимо в дополнение что бы Sy=0 и Sz=0.
4. При повороте взаимно перпендикулярных осей “y”и”z” относительно общего начала координат сумма осевых моментов инерции (Jy+Jz): (а) зависит от угла поворота; (б) не изменяется; (в) равна нулю; (г)изменяется, но не зависит от угла поворота. Ответ: (б) сумма осевых моментов относительно двух ортогональных осей при их повороте остаётся постоянной величиной, равной полярному моменту инерции Jр=
5. Ось “y” изменила своё направление на противоположное. Значение какого момента инерции изменится: (а) Jy; (б) Jz; (в) Dyz; (г) Jp;
6. Осевой момент инерции для треугольника будет максимальным для: (а) z0; (б) z1; Ответ: (г), поскольку наименьшее значение осевой момент Jz имеет для центральной оси z0, а значение осевого момента инерции для оси, параллельной цен-тральной возрастает на величину равную произведе-
нию площади фигуры на квадрат расстояния между осями.
Контрольные тесты 1.Если Jy=Jz и Dzy=0, то главные оси инерции наклонены к исходным осям под углом: (а) α = 90˚; (б) α = 30˚; (в) α = 45˚; (г) α = 60˚; 2. Выражение центробежного момента инерции плоского сечения относительно осей “y”и “z” имеет вид: (а) 3. Центробежный момент инерции сечения относительно главных осей:
(а) Dzy > 0; (б) Dzy=0; (в) Dzy < 0; (г) Dzy
4. Осевой момент инерции круглого сплошного сечения определяется по формуле: (а) 5.Положение главных осей инерции определяется углом α0, а tg 2α0 равен: (а) 6.Осевой момент инерции треугольника высотой h и основанием b относительно оси “z”, проходящей через основание определяется по формуле: (а) 7. Если Jy < Jz, то при повороте осей на угол α0 главная ось инерции, ближайшая к оси “z” будет осью: (а) симметрии; (б) максимума; (в) минимума; (г) нейтральной.
8. При повороте осей на угол α, осевой момент инерции Jy, относительно повёрнутой оси “y”, можно вычислить по формуле:
(а) Jz cos2α + Jy sin2α - Dyz sin2α; (б) Jy cos2α + Jz sin2α + Dyz sin2α; (в) Dyz cos2α - НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 465; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.4.239 (0.054 с.) |
 сводим к интегрированию по одной переменной:
сводим к интегрированию по одной переменной: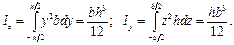
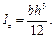

 Треугольник. Найдем момент инерции Iz отно-сительно оси, проходящей через центр тяжести (рис.3.3). Очевидно, ширина элементарной полоски, находящейся на расстоянии у от оси z, равна:
Треугольник. Найдем момент инерции Iz отно-сительно оси, проходящей через центр тяжести (рис.3.3). Очевидно, ширина элементарной полоски, находящейся на расстоянии у от оси z, равна: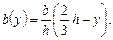
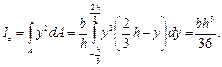
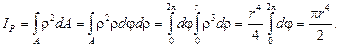
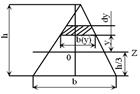
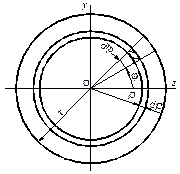 Учитывая, что полярный момент инерции равен сумме двух осевых моментов, и принимая во внимание осевую симметрию, получаем
Учитывая, что полярный момент инерции равен сумме двух осевых моментов, и принимая во внимание осевую симметрию, получаем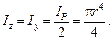
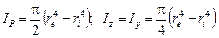
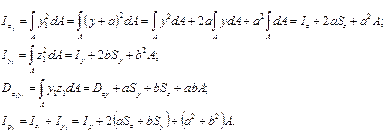
 , и
, и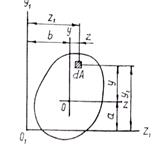
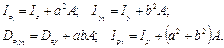
 ) имеют наименьшие значения по сравнению с моментами инерции относительно любых других параллельных осей.
) имеют наименьшие значения по сравнению с моментами инерции относительно любых других параллельных осей.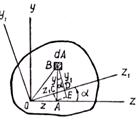
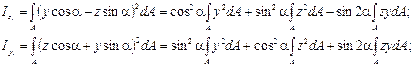
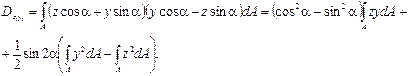
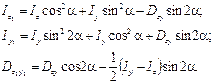
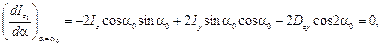

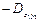 . Оси, относительно которых осевые моменты инерции принимают экстремальные значения (при этом центробежный момент инерции становится равным нулю), называют главными осями инерции сечения. Для их определения используют зависимость, получаемую из последнего уравнения:
. Оси, относительно которых осевые моменты инерции принимают экстремальные значения (при этом центробежный момент инерции становится равным нулю), называют главными осями инерции сечения. Для их определения используют зависимость, получаемую из последнего уравнения:
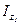 , используя при этом формулы тригонометрии:
, используя при этом формулы тригонометрии:

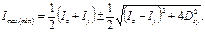
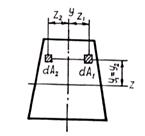 Равенство нулю центробежного момента инерции относительно главных осей часто используют для их непосредственного определения. Так, например, для симметричной фигуры ось симметрии является главной осью, поскольку центробежные моменты инерции площадок dA 1 и dA 2 (рис.3.7) при z 2 = – z 1 в сумме дают нуль, в силу чего и для всего сечения величина Dzy равна нулю. Таким образом, одна главная ось – ось симметрии у, другая перпендикулярна ей. Главные оси инерции можно провести через любую точку, взятую в плоскости сечения. Однако практическое значение для расчета элементов конструкций имеют лишь главные центральные оси инерции, проходящие через центр тяжести сечения, который совпадает с осью бруса (стержня) и является центром приведения внутренних
Равенство нулю центробежного момента инерции относительно главных осей часто используют для их непосредственного определения. Так, например, для симметричной фигуры ось симметрии является главной осью, поскольку центробежные моменты инерции площадок dA 1 и dA 2 (рис.3.7) при z 2 = – z 1 в сумме дают нуль, в силу чего и для всего сечения величина Dzy равна нулю. Таким образом, одна главная ось – ось симметрии у, другая перпендикулярна ей. Главные оси инерции можно провести через любую точку, взятую в плоскости сечения. Однако практическое значение для расчета элементов конструкций имеют лишь главные центральные оси инерции, проходящие через центр тяжести сечения, который совпадает с осью бруса (стержня) и является центром приведения внутренних

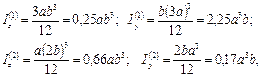
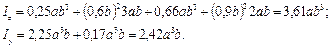
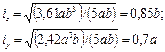
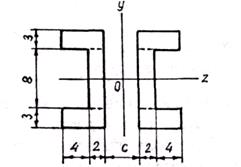
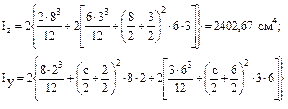 Рис. 3.9
Рис. 3.9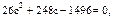
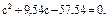
 0.
0.  2. Для какой из осей статический момент сечения S будет наибольшим:
2. Для какой из осей статический момент сечения S будет наибольшим: 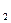 > Sy поскольку элементарные площадки удалены на расстояния, большие чем от оси “у”, а из осей х1, х2, х3 статический момент имеет большую величину для наиболее удалённой оси.
> Sy поскольку элементарные площадки удалены на расстояния, большие чем от оси “у”, а из осей х1, х2, х3 статический момент имеет большую величину для наиболее удалённой оси. ρ2 dA.
ρ2 dA. Ответ: (в), величина центробежного момента сохранится, но знак изменится на противоположный. Для других моментов инерции “x”,”y”, координаты стоят под интегралом в квадрате, следовательно будет координата “+y” или ”-у” – величина момента не изменится.
Ответ: (в), величина центробежного момента сохранится, но знак изменится на противоположный. Для других моментов инерции “x”,”y”, координаты стоят под интегралом в квадрате, следовательно будет координата “+y” или ”-у” – величина момента не изменится. (в) z2; (г) z3;
(в) z2; (г) z3;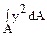 ; (б)
; (б) 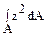 ; (в)
; (в) 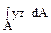 ; (г)
; (г) 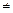 0.
0.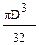 ; (б)
; (б) 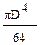 ; (в)
; (в) 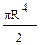 ; (г)
; (г) 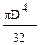 .
.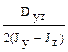 ; (б)
; (б) 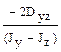 ; (в)
; (в) 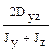 ; (г)
; (г) 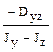 .
.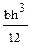 ; (б)
; (б) 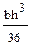 ; (в)
; (в) 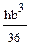 ; (г)
; (г) 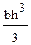 .
.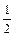 (Jy-Jz) sin2α; (г) Jz cos2α + Jy sin2α - Dyz sin2α
(Jy-Jz) sin2α; (г) Jz cos2α + Jy sin2α - Dyz sin2α


